人教新课标A版选修2-1第三章 空间向量与立体几何3.1.5 空间向量运算的坐标表示(21张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第三章 空间向量与立体几何3.1.5 空间向量运算的坐标表示(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 972.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 16:03:33 | ||
图片预览



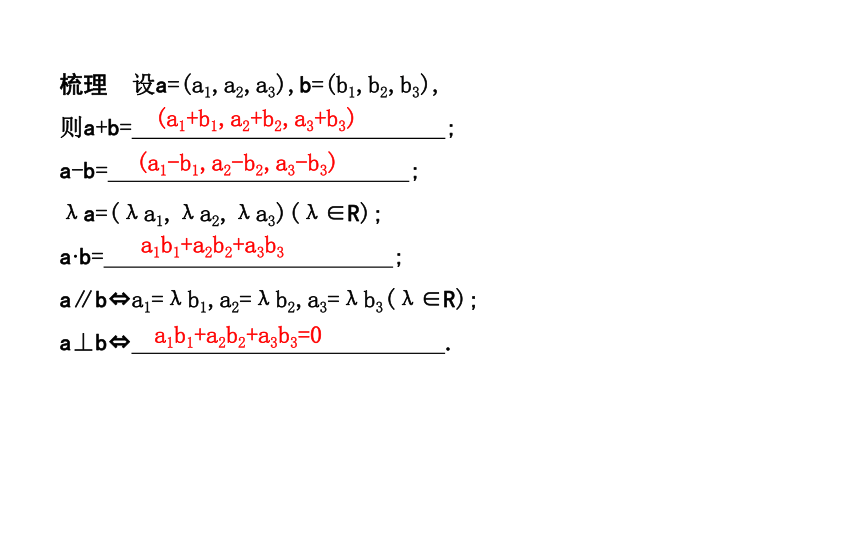





文档简介
课件21张PPT。3.1.5 空间向量运算的坐标表示新知探求 素养养成知识点一已知在单位正交基底{i,j,k}下,向量 a=(a1,a2,a3),b=(b1,b2,b3).
问题:向量a+b,a-b的坐标分别是如何推导的?空间向量运算的坐标表示答案:a+b=(a1i+a2j+a3k)+(b1i+b2j+b3k)=(a1+b1)i+(a2+b2)j+(a3+b3)k,故a+b=(a1+b1,a2+b2,a3+b3),同理有a-b=(a1-b1,a2-b2,a3-b3).梳理 设a=(a1,a2,a3),b=(b1,b2,b3),
则a+b= ;
a-b= ;
λa=(λa1,λa2,λa3)(λ∈R);
a·b= ;
a∥b?a1=λb1,a2=λb2,a3=λb3(λ∈R);
a⊥b? .(a1+b1,a2+b2,a3+b3)(a1-b1,a2-b2,a3-b3)a1b1+a2b2+a3b3a1b1+a2b2+a3b3=0知识点二空间向量夹角和距离的坐标计算公式梳理 (1)夹角公式
设a=(a1,a2,a3),b=(b1,b2,b3),
则cos= .题型一 空间向量的坐标运算课堂探究 素养提升方法技巧题型二 利用向量解决平行与垂直问题(2)若ka+b与ka-2b互相垂直,求k.一题多变:将本例(2)中“若ka+b与ka-2b互相垂直”改为“若ka+b与a+kb互相平行”,其他条件不变,求k的值.解:a=(1,1,0),b=(-1,0,2),所以ka+b=(k,k,0)+(-1,0,2)=(k-1,k,2),
a+kb=(1,1,0)+(-k,0,2k)=(1-k,1,2k),
因为ka+b与a+kb平行,所以ka+b=λ(a+kb)(λ∈R),
即(k-1,k,2)=λ(1-k,1,2k),方法技巧 向量平行与垂直问题的两种类型
(1)平行与垂直的判断
①应用向量的方法判定两直线平行,只需判断两直线的方向向量是否共线;②判断两直线是否垂直,关键是判断两直线的方向向量是否垂直,即判断两向量的数量积是否为0.
(2)利用平行与垂直求参数或其他问题,即平行与垂直的应用.解题时要注意:①适当引入参数(比如向量a,b平行,可设a=λb),建立关于参数的方程;②选择坐标形式,以达到简化运算的目的.题型三 利用向量的坐标形式求夹角与距离方法技巧 (1)求空间中两向量夹角的方法
①基向量法:结合图形,选取一组合适的基底,将两向量用基向量表示出来,然后代入夹角公式求解;②坐标法:在图形中建立空间直角坐标系,然后求出两向量的坐标,代入向量的夹角坐标公式求解.利用坐标法要注意两点,一是坐标系的选取,二是要注意夹角的范围∈[0,π],要特别关注向量共线的情况.
(2)求空间中线段的长
①建立恰当的空间直角坐标系;②求出线段端点的坐标,并求出对应向量的坐标;③利用向量的模的坐标公式求向量的模,即线段的长.答案:(1)B(2)正方体ABCD-A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|= 3|NC1|,则MN的长为 .?解析:(2)如图,以D为顶点,DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴建立空间直角坐标系Dxyz,则A1(4,0,4),B(4,4,0),
C1(0,4,4),D1(0,0,4).
因为M为BD1的中点,所以M(2,2,2),
因为N在A1C1上,且|A1N|=3|NC1|,题型四 易错辨析——由向量的夹角求参数的取值范围时忽略隐含或限制条件而致误纠错:解答本题易出现的失误是忽视了a·b<0包含a与b夹角为180°的情况,即a与b的夹角为钝角不等价于a·b<0.谢谢观赏!
问题:向量a+b,a-b的坐标分别是如何推导的?空间向量运算的坐标表示答案:a+b=(a1i+a2j+a3k)+(b1i+b2j+b3k)=(a1+b1)i+(a2+b2)j+(a3+b3)k,故a+b=(a1+b1,a2+b2,a3+b3),同理有a-b=(a1-b1,a2-b2,a3-b3).梳理 设a=(a1,a2,a3),b=(b1,b2,b3),
则a+b= ;
a-b= ;
λa=(λa1,λa2,λa3)(λ∈R);
a·b= ;
a∥b?a1=λb1,a2=λb2,a3=λb3(λ∈R);
a⊥b? .(a1+b1,a2+b2,a3+b3)(a1-b1,a2-b2,a3-b3)a1b1+a2b2+a3b3a1b1+a2b2+a3b3=0知识点二空间向量夹角和距离的坐标计算公式梳理 (1)夹角公式
设a=(a1,a2,a3),b=(b1,b2,b3),
则cos
a+kb=(1,1,0)+(-k,0,2k)=(1-k,1,2k),
因为ka+b与a+kb平行,所以ka+b=λ(a+kb)(λ∈R),
即(k-1,k,2)=λ(1-k,1,2k),方法技巧 向量平行与垂直问题的两种类型
(1)平行与垂直的判断
①应用向量的方法判定两直线平行,只需判断两直线的方向向量是否共线;②判断两直线是否垂直,关键是判断两直线的方向向量是否垂直,即判断两向量的数量积是否为0.
(2)利用平行与垂直求参数或其他问题,即平行与垂直的应用.解题时要注意:①适当引入参数(比如向量a,b平行,可设a=λb),建立关于参数的方程;②选择坐标形式,以达到简化运算的目的.题型三 利用向量的坐标形式求夹角与距离方法技巧 (1)求空间中两向量夹角的方法
①基向量法:结合图形,选取一组合适的基底,将两向量用基向量表示出来,然后代入夹角公式求解;②坐标法:在图形中建立空间直角坐标系,然后求出两向量的坐标,代入向量的夹角坐标公式求解.利用坐标法要注意两点,一是坐标系的选取,二是要注意夹角的范围
(2)求空间中线段的长
①建立恰当的空间直角坐标系;②求出线段端点的坐标,并求出对应向量的坐标;③利用向量的模的坐标公式求向量的模,即线段的长.答案:(1)B(2)正方体ABCD-A1B1C1D1的棱长为4,M为BD1的中点,N在A1C1上,且|A1N|= 3|NC1|,则MN的长为 .?解析:(2)如图,以D为顶点,DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴建立空间直角坐标系Dxyz,则A1(4,0,4),B(4,4,0),
C1(0,4,4),D1(0,0,4).
因为M为BD1的中点,所以M(2,2,2),
因为N在A1C1上,且|A1N|=3|NC1|,题型四 易错辨析——由向量的夹角求参数的取值范围时忽略隐含或限制条件而致误纠错:解答本题易出现的失误是忽视了a·b<0包含a与b夹角为180°的情况,即a与b的夹角为钝角不等价于a·b<0.谢谢观赏!
