人教新课标A版选修2-1第一章 常用逻辑用语第1章章末总结(30张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第一章 常用逻辑用语第1章章末总结(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览











文档简介
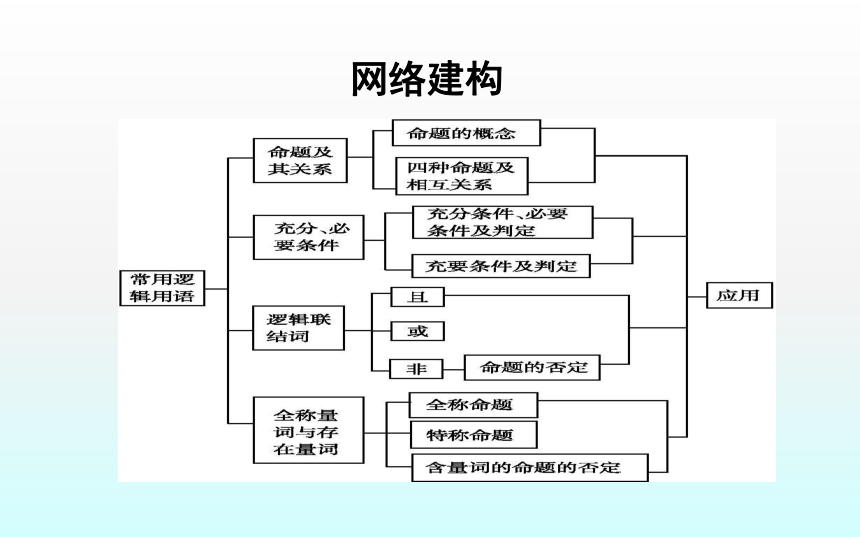
课件30张PPT。章末总结网络建构知识辨析×√判断下列说法是否正确.(请在括号中填“√”或“×”)
1.“x>0”是命题.( )
2.一个命题的逆命题和这个命题的否命题是互为逆否命题.( )
3.互逆、互否的两个命题真假性没有关系.( )
4.若A是B的充分条件,C是B的必要条件,则A是C的必要条件.( )
5.设命题p,q对应的集合分别为A,B,若p是q的充分不必要的条件,则B A.
( )
6.“若p,则q”的否定为“若﹁p,则﹁q”.( )
7.“三角形都存在一个外接圆”中的“存在”为特称量词.( )√××××题型一命题的关系及其真假判定题型归纳 素养提升【典例1】 (1) (2018·洛阳高二期中)已知命题“若{an}是常数列,则{an}是等差数列”,在其逆命题、否命题和逆否命题中,假命题的个数是 ;?(1)解析:若{an}是常数列,则{an}是等差数列正确,即原命题正确,则逆否命题也正确.
命题的逆命题为若{an}是等差数列,则{an}是常数列,
当公差d≠0时,{an}不是常数列,故逆命题为假命题,则否命题为假命题,故假命题的个数为2.答案:2(2)已知a,b,c∈R,写出命题“若ac<0,则方程ax2+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题,并判断这三个命题的真假.(2)解:逆命题“若方程ax2+bx+c=0(a,b,c∈R)有两个不相等的实数根,则ac<0”,是假命题.
如当a=1,b=-3,c=2时,方程x2-3x+2=0有两个不等实根x1=1,x2=2,但ac=2>0.
否命题“若ac≥0,则方程ax2+bx+c=0(a,b,c∈R)没有两个不相等的实数根”,是假命题.
这是因为它和逆命题互为逆否命题,而逆命题是假命题.
逆否命题“若方程ax2+bx+c=0(a,b,c∈R)没有两个不相等的实数根,则ac≥0”,是真命题.
因为原命题是真命题,而逆否命题与原命题等价.规律方法 (1)对四种命题的真假判断,一般先改写成“若p,则q”的形式,再判断或利用等价命题进行判断.
(2)对于特称或全称命题真假的判断,涉及指数函数、二次函数和三角函数等知识点,但难度不大,处理此类问题的关键是准确利用所学知识逐个进行判断,灵活采用各种判断方法.题型二充分必要条件的判定(A)充分非必要条件 (B)必要非充分条件
(C)非充分非必要条件 (D)充要条件(2)(2018·武汉二中高二期末)“a=-2”是“直线(a+2)x+3ay+1=0与直线(a-2)x+
(a+2)y-3=0相互垂直”的( )
(A)充要条件 (B)充分非必要条件
(C)必要非充分条件 (D)既非充分也非必要条件规律方法 判断充分必要条件时关键是要分清命题的条件与结论,如果从正面判断或证明一个命题的正确或错误不易进行时,可以通过举出恰当的特例来说明.题型三 含逻辑联结词的命题(A)p为真 (B)﹁p为假
(C)p∧q为假 (D)p∨q为真(1)解析:p假,q假,故选C.(2)设集合A={x|-2-a0},命题p:1∈A,命题q:2∈A.若p∨q为真命题,p∧q为假命题,求a的取值范围.规律方法 判断含有逻辑联结词的命题真假的方法
(1)先确定简单命题p,q.
(2)分别确定简单命题p,q的真假.
(3)利用真值表判断所给命题的真假.题型四 命题的否定与否命题(2)写出下列各命题的否定及其否命题,并判断它们的真假.
①若x,y都是奇数,则x+y是偶数;
②若一个数是质数,则这个数是奇数.(2)解:①命题的否定:x,y都是奇数,则x+y不是偶数,为假命题.
原命题的否命题:若x,y不都是奇数,则x+y不是偶数,是假命题.
②命题的否定:若一个数是质数,则这个数不是奇数,是假命题.
原命题的否命题:若一个数不是质数,则这个数不是奇数,为假命题.规律方法 (1)命题的否定只否定结论;
(2)否命题对条件和结论都要否定.题型五 等价转化思想【典例5】 设集合A={x|-x2+x+6≤0},关于x的不等式x2-ax-2a2>0的解集为B(其中a<0).
(1)求集合B;解:(1)x2-ax-2a2>0?(x-2a)(x+a)>0,
解得x>-a或x<2a.
故集合B={x|x>-a或x<2a}(a<0).(2)设p:x∈A,q:x∈B,且﹁p是﹁q的必要不充分条件,求实数a的取值范围.规律方法 本题通过“﹁q?﹁p”(若﹁q,则﹁p)得到p?q(若p,则q),用到了等价转化的思想,利用命题的等价性解题,在求一些参数的范围问题时,显得简单快捷.题型六 易错辨析1.不能准确判断充要条件
【典例6】 判断下列各题中的条件p是结论q的什么条件.
条件p:ax2+ax+1>0的解集是R.
结论q:0所以当00恒成立,故q?p.
当ax2+ax+1>0的解集是R时,有0所以p是q的充要条件.纠错:此类题目的易错点是在用定义判断时,忽略了无论是p?q,还是q?p,均要认真考虑是否有反例,这一点往往是判断充分性和必要性的关键和难点.题中,根据一元二次不等式的解法考虑此题,忽略了a=0时原不等式变为1>0这一绝对不等式的情况.2.对命题的否定不全面真题体验1.(2015·全国Ⅰ卷)设命题p:?n∈N,n2>2n,则﹁p为( )
(A)?n∈N,n2>2n (B)?n∈N,n2≤2n
(C)?n∈N,n2≤2n (D)?n∈N,n2=2nC解析:由特称命题的否定为全称命题知选C.2.设m,n为非零向量,则“存在负数λ,使得m=λn”是“m·n<0”的( )
(A)充分而不必要条件
(B)必要而不充分条件
(C)充分必要条件
(D)既不充分也不必要条件解析:若λ<0,不妨取λ=-1,则m=λn表示非零向量m,n反向共线,必有m·n<0;反之,若m·n<0,非零向量m,n不一定反向共线(可能夹角为钝角),也就是不一定有m=λn,所以“存在负数λ,使得m=λn”是“m·n<0”的充分而不必要条件,故选A.A3.已知命题p:?x>0,ln (x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( )
(A)p∧q (B)p∧﹁q (C)﹁p∧q (D)p∧﹁qB解析:因为x>0,所以+1>1,所以ln (x+1)>ln 1=0.
所以命题p为真命题,所以﹁为假命题.
因为a>b,取a=1,b=-2,而12=1,(-2)2=4,
因此a2所以命题q为假命题,所以﹁q为真命题.
所以q∧q为假命题,p∧﹁q为真命题,﹁p∧q为假命题,﹁p∧﹁q为假命题.故选B.4.已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4+S6>2S5”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件解析:因为S4+S6>2S5?S4+S4+a5+a6>2(S4+a5)?a6>a5?a5+d>a5?d>0,
所以“d>0”是“S4+S6>2S5”的充分必要条件.故选C.C5.命题“?x∈R,?n∈N*,使得n≥x2”的否定形式是( )
(A)?x∈R,?n∈N*,使得n(B)?x∈R,?n∈N*,使得n(C)?x∈R,?n∈N*,使得n(D)?x∈R,?n∈N*,使得n②单位圆上的点的“伴随点”仍在单位圆上;
③若两点关于x轴对称,则它们的“伴随点”关于y轴对称;
④若三点在同一条直线上,则它们的“伴随点”一定共线.
其中的真命题是 (写出所有真命题的序号).?②设P(x,y),其中x2+y2=1,则其伴随点为(y,-x),该点也在圆x2+y2=1上,故②正确.答案:②③谢谢观赏!
1.“x>0”是命题.( )
2.一个命题的逆命题和这个命题的否命题是互为逆否命题.( )
3.互逆、互否的两个命题真假性没有关系.( )
4.若A是B的充分条件,C是B的必要条件,则A是C的必要条件.( )
5.设命题p,q对应的集合分别为A,B,若p是q的充分不必要的条件,则B A.
( )
6.“若p,则q”的否定为“若﹁p,则﹁q”.( )
7.“三角形都存在一个外接圆”中的“存在”为特称量词.( )√××××题型一命题的关系及其真假判定题型归纳 素养提升【典例1】 (1) (2018·洛阳高二期中)已知命题“若{an}是常数列,则{an}是等差数列”,在其逆命题、否命题和逆否命题中,假命题的个数是 ;?(1)解析:若{an}是常数列,则{an}是等差数列正确,即原命题正确,则逆否命题也正确.
命题的逆命题为若{an}是等差数列,则{an}是常数列,
当公差d≠0时,{an}不是常数列,故逆命题为假命题,则否命题为假命题,故假命题的个数为2.答案:2(2)已知a,b,c∈R,写出命题“若ac<0,则方程ax2+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题,并判断这三个命题的真假.(2)解:逆命题“若方程ax2+bx+c=0(a,b,c∈R)有两个不相等的实数根,则ac<0”,是假命题.
如当a=1,b=-3,c=2时,方程x2-3x+2=0有两个不等实根x1=1,x2=2,但ac=2>0.
否命题“若ac≥0,则方程ax2+bx+c=0(a,b,c∈R)没有两个不相等的实数根”,是假命题.
这是因为它和逆命题互为逆否命题,而逆命题是假命题.
逆否命题“若方程ax2+bx+c=0(a,b,c∈R)没有两个不相等的实数根,则ac≥0”,是真命题.
因为原命题是真命题,而逆否命题与原命题等价.规律方法 (1)对四种命题的真假判断,一般先改写成“若p,则q”的形式,再判断或利用等价命题进行判断.
(2)对于特称或全称命题真假的判断,涉及指数函数、二次函数和三角函数等知识点,但难度不大,处理此类问题的关键是准确利用所学知识逐个进行判断,灵活采用各种判断方法.题型二充分必要条件的判定(A)充分非必要条件 (B)必要非充分条件
(C)非充分非必要条件 (D)充要条件(2)(2018·武汉二中高二期末)“a=-2”是“直线(a+2)x+3ay+1=0与直线(a-2)x+
(a+2)y-3=0相互垂直”的( )
(A)充要条件 (B)充分非必要条件
(C)必要非充分条件 (D)既非充分也非必要条件规律方法 判断充分必要条件时关键是要分清命题的条件与结论,如果从正面判断或证明一个命题的正确或错误不易进行时,可以通过举出恰当的特例来说明.题型三 含逻辑联结词的命题(A)p为真 (B)﹁p为假
(C)p∧q为假 (D)p∨q为真(1)解析:p假,q假,故选C.(2)设集合A={x|-2-a
(1)先确定简单命题p,q.
(2)分别确定简单命题p,q的真假.
(3)利用真值表判断所给命题的真假.题型四 命题的否定与否命题(2)写出下列各命题的否定及其否命题,并判断它们的真假.
①若x,y都是奇数,则x+y是偶数;
②若一个数是质数,则这个数是奇数.(2)解:①命题的否定:x,y都是奇数,则x+y不是偶数,为假命题.
原命题的否命题:若x,y不都是奇数,则x+y不是偶数,是假命题.
②命题的否定:若一个数是质数,则这个数不是奇数,是假命题.
原命题的否命题:若一个数不是质数,则这个数不是奇数,为假命题.规律方法 (1)命题的否定只否定结论;
(2)否命题对条件和结论都要否定.题型五 等价转化思想【典例5】 设集合A={x|-x2+x+6≤0},关于x的不等式x2-ax-2a2>0的解集为B(其中a<0).
(1)求集合B;解:(1)x2-ax-2a2>0?(x-2a)(x+a)>0,
解得x>-a或x<2a.
故集合B={x|x>-a或x<2a}(a<0).(2)设p:x∈A,q:x∈B,且﹁p是﹁q的必要不充分条件,求实数a的取值范围.规律方法 本题通过“﹁q?﹁p”(若﹁q,则﹁p)得到p?q(若p,则q),用到了等价转化的思想,利用命题的等价性解题,在求一些参数的范围问题时,显得简单快捷.题型六 易错辨析1.不能准确判断充要条件
【典例6】 判断下列各题中的条件p是结论q的什么条件.
条件p:ax2+ax+1>0的解集是R.
结论q:0
当ax2+ax+1>0的解集是R时,有0
(A)?n∈N,n2>2n (B)?n∈N,n2≤2n
(C)?n∈N,n2≤2n (D)?n∈N,n2=2nC解析:由特称命题的否定为全称命题知选C.2.设m,n为非零向量,则“存在负数λ,使得m=λn”是“m·n<0”的( )
(A)充分而不必要条件
(B)必要而不充分条件
(C)充分必要条件
(D)既不充分也不必要条件解析:若λ<0,不妨取λ=-1,则m=λn表示非零向量m,n反向共线,必有m·n<0;反之,若m·n<0,非零向量m,n不一定反向共线(可能夹角为钝角),也就是不一定有m=λn,所以“存在负数λ,使得m=λn”是“m·n<0”的充分而不必要条件,故选A.A3.已知命题p:?x>0,ln (x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是( )
(A)p∧q (B)p∧﹁q (C)﹁p∧q (D)p∧﹁qB解析:因为x>0,所以+1>1,所以ln (x+1)>ln 1=0.
所以命题p为真命题,所以﹁为假命题.
因为a>b,取a=1,b=-2,而12=1,(-2)2=4,
因此a2
所以q∧q为假命题,p∧﹁q为真命题,﹁p∧q为假命题,﹁p∧﹁q为假命题.故选B.4.已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4+S6>2S5”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件解析:因为S4+S6>2S5?S4+S4+a5+a6>2(S4+a5)?a6>a5?a5+d>a5?d>0,
所以“d>0”是“S4+S6>2S5”的充分必要条件.故选C.C5.命题“?x∈R,?n∈N*,使得n≥x2”的否定形式是( )
(A)?x∈R,?n∈N*,使得n
③若两点关于x轴对称,则它们的“伴随点”关于y轴对称;
④若三点在同一条直线上,则它们的“伴随点”一定共线.
其中的真命题是 (写出所有真命题的序号).?②设P(x,y),其中x2+y2=1,则其伴随点为(y,-x),该点也在圆x2+y2=1上,故②正确.答案:②③谢谢观赏!
