人教新课标A版选修2-1第二章 圆锥曲线与方程第2章末总结(34张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第二章 圆锥曲线与方程第2章末总结(34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 16:42:33 | ||
图片预览











文档简介
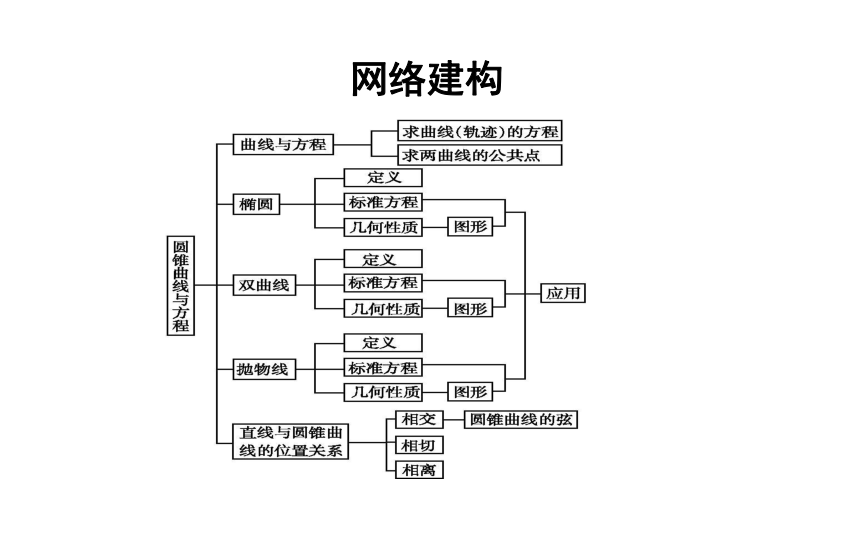
课件34张PPT。章末总结网络建构知识辨析×√×××√√题型一求曲线方程题型归纳 素养提升【典例1】 设圆(x-1)2+y2=1的圆心为C,过原点作圆的弦OA,求OA中点B的轨迹方程.规律方法 (1)解决轨迹问题要明确圆锥曲线的性质,做好对图形变化情况的总体分析,选好相应的解题策略、具体方法,注意将动点的几何特性用数学语言表述.
(2)要注意轨迹问题所包含的隐含条件,也就是曲线上点的坐标的取值 范围.题型二圆锥曲线的定义及性质规律方法 “回归定义”解题的三点应用
应用一:在求轨迹方程时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的定义,写出所求的轨迹方程;
应用二:涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决;
应用三:在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决.题型三 直线与圆锥曲线的位置关系规律方法 直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称,取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法;还要多结合圆锥曲线的定义,根与系数的关系以及“点差法”等.题型四 圆锥曲线中的定点、定值、最值问题(2)过原点O的动直线(与坐标轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点,问以MN为直径的圆是否经过定点?请证明你的结论.规律方法 圆锥曲线中的最值问题,通常有两类:一类是有关长度、面积等最值问题;一类是圆锥曲线中有关几何元素的最值问题,这两类问题的解决往往通过回归定义,结合几何知识,建立目标函数,利用函数的性质或不等式知识,以及数形结合、设参、转化、代换等途径来解决.题型五 易错辨析1.忽略了对答案的验证致误
【典例5】 已知双曲线2x2-y2=2,过点B(1,1)能否作直线l,使l与所给双曲线交于点Q1,Q2,且点B是弦Q1Q2的中点.若存在这样的直线l,求出它的方程;若不存在,说明理由.纠错:通过数形分析发现所求得的直线与双曲线不一定有交点,对于这种情况要进行检验,在解析几何中凡是直线与圆锥曲线相交问题先考虑相交的前提,否则易产生错解.
正解:由错解可知可能存在的直线l方程为y-1=2(x-1),即2x-y-1=0,与双曲线方程联立消去y得2x2-4x+3=0,而Δ=-8<0,则方程无实根,即直线与双曲线无交点,故不存在满足条件的直线.2.忽略分类讨论而致误
【典例6】 求过定点P(0,1)且与抛物线y2=2x只有一个公共点的直线方程.纠错:本题造成错解的原因有两个:一是遗漏了直线斜率不存在的情况,只考虑了斜率存在的直线;二是把方程组消元后的方程误认为是二次方程,事实上,二次项系数为零的一次方程的解也符合题意.真题体验1.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( )
(A)16 (B)14
(C)12 (D)10AA A 4.已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则|FN|= .?答案:6(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.谢谢观赏!
(2)要注意轨迹问题所包含的隐含条件,也就是曲线上点的坐标的取值 范围.题型二圆锥曲线的定义及性质规律方法 “回归定义”解题的三点应用
应用一:在求轨迹方程时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的定义,写出所求的轨迹方程;
应用二:涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决;
应用三:在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决.题型三 直线与圆锥曲线的位置关系规律方法 直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称,取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法;还要多结合圆锥曲线的定义,根与系数的关系以及“点差法”等.题型四 圆锥曲线中的定点、定值、最值问题(2)过原点O的动直线(与坐标轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点,问以MN为直径的圆是否经过定点?请证明你的结论.规律方法 圆锥曲线中的最值问题,通常有两类:一类是有关长度、面积等最值问题;一类是圆锥曲线中有关几何元素的最值问题,这两类问题的解决往往通过回归定义,结合几何知识,建立目标函数,利用函数的性质或不等式知识,以及数形结合、设参、转化、代换等途径来解决.题型五 易错辨析1.忽略了对答案的验证致误
【典例5】 已知双曲线2x2-y2=2,过点B(1,1)能否作直线l,使l与所给双曲线交于点Q1,Q2,且点B是弦Q1Q2的中点.若存在这样的直线l,求出它的方程;若不存在,说明理由.纠错:通过数形分析发现所求得的直线与双曲线不一定有交点,对于这种情况要进行检验,在解析几何中凡是直线与圆锥曲线相交问题先考虑相交的前提,否则易产生错解.
正解:由错解可知可能存在的直线l方程为y-1=2(x-1),即2x-y-1=0,与双曲线方程联立消去y得2x2-4x+3=0,而Δ=-8<0,则方程无实根,即直线与双曲线无交点,故不存在满足条件的直线.2.忽略分类讨论而致误
【典例6】 求过定点P(0,1)且与抛物线y2=2x只有一个公共点的直线方程.纠错:本题造成错解的原因有两个:一是遗漏了直线斜率不存在的情况,只考虑了斜率存在的直线;二是把方程组消元后的方程误认为是二次方程,事实上,二次项系数为零的一次方程的解也符合题意.真题体验1.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( )
(A)16 (B)14
(C)12 (D)10AA A 4.已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则|FN|= .?答案:6(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.谢谢观赏!
