人教新课标A版选修2-1第三章 空间向量与立体几何3.2立体几何中的向量方法(三)向量法 PPT(17张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第三章 空间向量与立体几何3.2立体几何中的向量方法(三)向量法 PPT(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 670.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 16:51:10 | ||
图片预览





文档简介
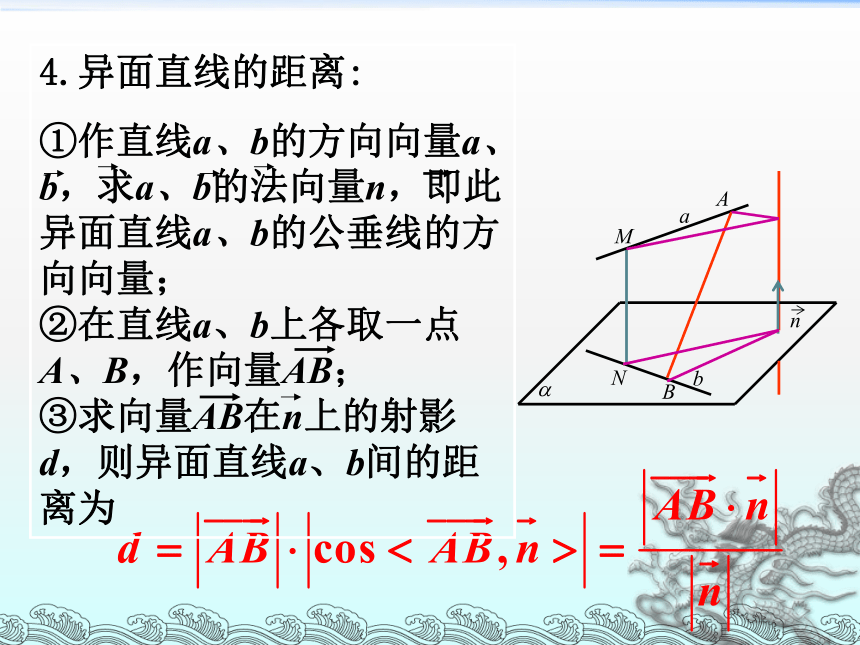
课件17张PPT。-----利用向量解决空间的距离问题3.2立体几何中的向量方法向量法求空间距离的求解方法1.空间中的距离主要有:两点间的距离、点到直线的距离、点到平面的距离、直线到平面的距离、平行平面的距离、异面直线间的距离.其中直线到平面的距离、平行平面的距离都可以转化点到平面的距离.
2.空间中两点间的距离:设A(x1,y1,z1),B(x2,y2,z3),则
3.求点到平面的距离:如图点P为平面外一点,
点A为平面内的任一点,平面的法向量为n,过
点P作平面?的垂线PO,记PA和平面?所成的
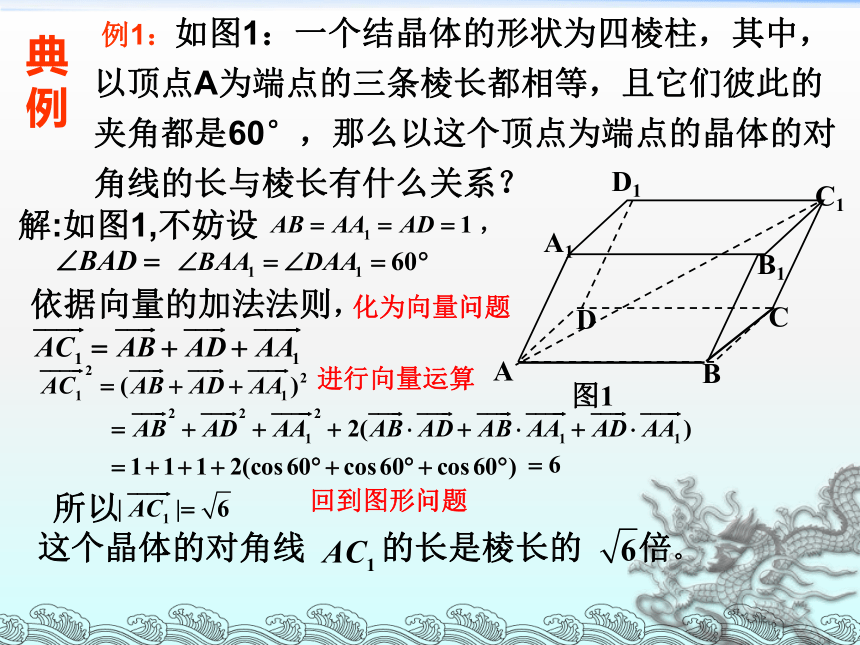
角为?,则点P到平面的距离n?APO?BAaMNnab 例1:如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,那么以这个顶点为端点的晶体的对角线的长与棱长有什么关系? 解:如图1,不妨设化为向量问题依据向量的加法法则,进行向量运算所以回到图形问题这个晶体的对角线 的长是棱长的 倍。典例思考:(1)本题中四棱柱的对角线BD1的长与棱长有什么关系? (2)如果一个四棱柱的各条棱长都相等,并且以某一顶点为端点的各棱间的夹角都等于 , 那么有这个四棱柱的对角线的长可以确定棱长吗? (3)本题的晶体中相对的两个平面之间的距离
是多少? (提示:求两个平行平面的距离,通常归结为求点到平面的距离或两点间的距离)思考(1)分析:思考(2)分析:∴ 这个四棱柱的对角线的长可以确定棱长.H 分析:面面距离转化为点面距离来求解:∴ 所求的距离是 思考(3)本题的晶体中相对的两个平面之间的距离是多少? 如何用向量法求点到平面的距离?(1) 求B1到面A1BE的距离;例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:(2) 求D1C到面A1BE的距离;解:∵D1C∥面A1BE
∴ D1到面A1BE的距离即为D1C到面A1BE的距离例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:(3) 求面A1DB与面D1CB1的距离;解:∵面D1CB1∥面A1BD
∴ D1到面A1BD的距离即为面D1CB1到面A1BD的距离例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:(4) 求异面直线D1B与A1E的距离.课堂练习:练习1:如图,空间四边形OABC各边以及AC,BO的长都是1,点D,E分别是边OA,BC的中点,连结DE,计算DE的长。 FEB1C1D1DCA练习2:
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是B1C1和C1D1 的中点,求点A1到平面DBEF的距离。BxyzA1练习3:
如图在直三棱柱ABC-A1B1C1中,AC=BC=1, ∠ACB=900,AA1= ,求B1到平面A1BC的距离。xyz小结 利用法向量来解决上述立体几何题目,最大的优点就是不用象在进行几何推理时那样去确定垂足的位置,完全依靠计算就可以解决问题。但是也有局限性,用代数推理解立体几何题目,关键就是得建立空间直角坐标系,把向量通过坐标形式表示出来,所以能用这种方法解题的立体几何模型一般都是如:正(长)方体、直棱柱、正棱锥等。作业P112 A组 5 9 补充作业:
已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB、AD的中点,求点B到平面GEF的距离。GBDACEFxyz
2.空间中两点间的距离:设A(x1,y1,z1),B(x2,y2,z3),则
3.求点到平面的距离:如图点P为平面外一点,
点A为平面内的任一点,平面的法向量为n,过
点P作平面?的垂线PO,记PA和平面?所成的
角为?,则点P到平面的距离n?APO?BAaMNnab 例1:如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°,那么以这个顶点为端点的晶体的对角线的长与棱长有什么关系? 解:如图1,不妨设化为向量问题依据向量的加法法则,进行向量运算所以回到图形问题这个晶体的对角线 的长是棱长的 倍。典例思考:(1)本题中四棱柱的对角线BD1的长与棱长有什么关系? (2)如果一个四棱柱的各条棱长都相等,并且以某一顶点为端点的各棱间的夹角都等于 , 那么有这个四棱柱的对角线的长可以确定棱长吗? (3)本题的晶体中相对的两个平面之间的距离
是多少? (提示:求两个平行平面的距离,通常归结为求点到平面的距离或两点间的距离)思考(1)分析:思考(2)分析:∴ 这个四棱柱的对角线的长可以确定棱长.H 分析:面面距离转化为点面距离来求解:∴ 所求的距离是 思考(3)本题的晶体中相对的两个平面之间的距离是多少? 如何用向量法求点到平面的距离?(1) 求B1到面A1BE的距离;例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:(2) 求D1C到面A1BE的距离;解:∵D1C∥面A1BE
∴ D1到面A1BE的距离即为D1C到面A1BE的距离例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:(3) 求面A1DB与面D1CB1的距离;解:∵面D1CB1∥面A1BD
∴ D1到面A1BD的距离即为面D1CB1到面A1BD的距离例2 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求下列问题:(4) 求异面直线D1B与A1E的距离.课堂练习:练习1:如图,空间四边形OABC各边以及AC,BO的长都是1,点D,E分别是边OA,BC的中点,连结DE,计算DE的长。 FEB1C1D1DCA练习2:
已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是B1C1和C1D1 的中点,求点A1到平面DBEF的距离。BxyzA1练习3:
如图在直三棱柱ABC-A1B1C1中,AC=BC=1, ∠ACB=900,AA1= ,求B1到平面A1BC的距离。xyz小结 利用法向量来解决上述立体几何题目,最大的优点就是不用象在进行几何推理时那样去确定垂足的位置,完全依靠计算就可以解决问题。但是也有局限性,用代数推理解立体几何题目,关键就是得建立空间直角坐标系,把向量通过坐标形式表示出来,所以能用这种方法解题的立体几何模型一般都是如:正(长)方体、直棱柱、正棱锥等。作业P112 A组 5 9 补充作业:
已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB、AD的中点,求点B到平面GEF的距离。GBDACEFxyz
