人教新课标A版选修2-1第三章 空间向量与立体几何第3章末总结(31张PPT)
文档属性
| 名称 | 人教新课标A版选修2-1第三章 空间向量与立体几何第3章末总结(31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 17:07:14 | ||
图片预览











文档简介
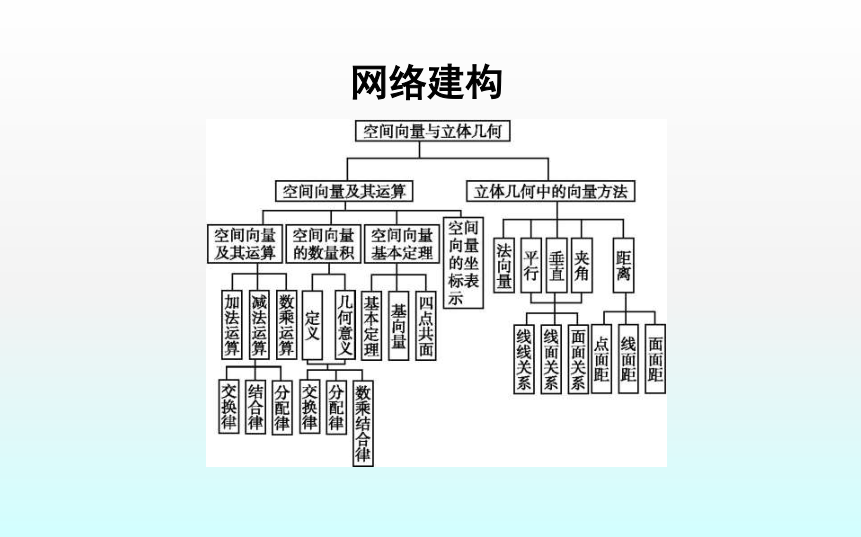
课件31张PPT。章末总结网络建构知识辨析× √ 3.若a·b=0,则a=0或b=0.( )
4.对非零向量a,b,c,若a·b=b·c,则a=c.( )
5.基向量可以是零向量.( )
6.空间中三个向量若有两个向量共线,则这三个向量一定共面.( )×××√ 7.设{a,b,c}是空间的一个基底,对空间任一向量p,使得p=xa+yb+zc成立的有序实数组{x,y,z}是唯一的.( )
8.若a·b<0,则一定是钝角.( )
9.设直线l与平面α所成的角为θ,l的方向向量为a,平面α的法向量为n,则sinθ=cos.( )√××题型一空间向量与线面位置关系题型归纳 素养提升【典例1】已知四棱锥P-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M点为PC的中点.
(1)求证:BM∥平面PAD;(2)在平面PAD内找一点N,使MN⊥平面PBD.规律方法 (1)证明两条直线平行,只需证明这两条直线的方向向量是共线向量.
(2)证明线面平行的方法
①证明直线的方向向量与平面的法向量垂直.
②能够在平面内找到一个向量与已知直线的方向向量共线.
③利用共面向量定理,即证明直线的方向向量与平面内的两个不共线向量是共面向量.
(3)证明面面平行的方法
①转化为线线平行、线面平行处理.
②证明这两个平面的法向量是共线向量.(4)证明两条直线垂直,只需证明这两条直线的方向向量垂直.
(5)证明线面垂直的方法
①证明直线的方向向量与平面的法向量是共线向量.
②证明直线的方向向量与平面内的两个不共线的向量互相垂直.
(6)证明面面垂直的方法
①转化为证明线面垂直.
②证明两个平面的法向量互相垂直.题型二用空间向量求角【典例2】如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;(2)求平面ADC1与平面ABA1所成二面角的正弦值.规律方法 利用空间向量求空间角的注意点
(1)异面直线所成的角:两异面直线所成角的范围为0°<θ≤90°,需找到两异面直线的方向向量,借助方向向量所成角求解.
(2)直线与平面所成的角:要求直线a与平面α所成的角θ,先求这个平面α的法向量n与直线a的方向向量a夹角的余弦cos,易知θ=-
或者 -.(3)二面角:如图,有两个平面α与β,分别作这两个平面的法向量n1与n2,则平面α与β所成的角跟法向量n1与n2所成的角相等或互补,所以首先应判断二面角是锐角还是钝角.题型三 用空间向量求距离【典例3】在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,M为BB1的中点,N为BC的中点.
(1)求点M到直线AC1的距离;(2)求点N到平面MA1C1的距离.规律方法 用向量法求空间距离
(1)点线距离的求法如图,在直线l上任取一点B,取直线l的一个方向向量e,则点A到l的距离为| |·sin< ,e>.
(2)点面距离的求法
如图,n是平面α的一个法向量,AB是平面α的一条斜线,则点B到平面α的距离为 .
(3)两平行平面间距离的求法
把求两平行平面间的距离转化为求点面距.
线面距也可转化为求点面距.题型四 易错辨析1.混淆向量与实数的运算性质致误
【典例4】已知a,b都是非零向量,且向量a+3b与7a-5b垂直,向量a-4b与7a-2b垂直,求向量a,b的夹角.纠错:向量的运算性质与实数不同,若b·(2a-b)=0不一定有b=0或2a-b=0,本题在此处误当作实数运算而导致了错误.2.对所求角与向量夹角的关系不理解致误
【典例5】正方体ABCD-A1B1C1D1中,求二面角A-BD1-C的大小.纠错:用法向量的夹角判断二面角的大小时出现错误,根据法向量的方向可知,二面角为钝角,而不是锐角.真题体验1.(2017·全国Ⅰ卷)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,从而AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD. (2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.2.(2017·全国Ⅱ卷)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D
的余弦值.3.(2017·全国Ⅲ卷)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;解:(1)由题设可得△ABD≌△CBD,从而AD=DC.又△ACD是直角三角形,所以∠ADC=90°.取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.所以∠DOB为二面角D-AC-B的平面角.在Rt△AOB中,BO2+AO2=AB2.又AB=BD,
所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.所以平面ACD⊥平面ABC.(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.4.(2016·山东卷)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;(1)证明:设FC的中点为I,连接GI,HI,
在△CEF中,因为点G,I分别是CE,CF的中点,
所以GI∥EF,又EF∥OB,所以GI∥OB,
在△CFB中,因为H,I分别是FB,CF的中点,
所以HI∥BC,又HI∩GI=I,所以平面GHI∥平面ABC,
因为GH?平面GHI,所以GH∥平面ABC.(2)已知EF=FB= AC= ,AB=BC,求二面角F-BC-A的余弦值.谢谢观赏!
4.对非零向量a,b,c,若a·b=b·c,则a=c.( )
5.基向量可以是零向量.( )
6.空间中三个向量若有两个向量共线,则这三个向量一定共面.( )×××√ 7.设{a,b,c}是空间的一个基底,对空间任一向量p,使得p=xa+yb+zc成立的有序实数组{x,y,z}是唯一的.( )
8.若a·b<0,则
9.设直线l与平面α所成的角为θ,l的方向向量为a,平面α的法向量为n,则sinθ=cos
(1)求证:BM∥平面PAD;(2)在平面PAD内找一点N,使MN⊥平面PBD.规律方法 (1)证明两条直线平行,只需证明这两条直线的方向向量是共线向量.
(2)证明线面平行的方法
①证明直线的方向向量与平面的法向量垂直.
②能够在平面内找到一个向量与已知直线的方向向量共线.
③利用共面向量定理,即证明直线的方向向量与平面内的两个不共线向量是共面向量.
(3)证明面面平行的方法
①转化为线线平行、线面平行处理.
②证明这两个平面的法向量是共线向量.(4)证明两条直线垂直,只需证明这两条直线的方向向量垂直.
(5)证明线面垂直的方法
①证明直线的方向向量与平面的法向量是共线向量.
②证明直线的方向向量与平面内的两个不共线的向量互相垂直.
(6)证明面面垂直的方法
①转化为证明线面垂直.
②证明两个平面的法向量互相垂直.题型二用空间向量求角【典例2】如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;(2)求平面ADC1与平面ABA1所成二面角的正弦值.规律方法 利用空间向量求空间角的注意点
(1)异面直线所成的角:两异面直线所成角的范围为0°<θ≤90°,需找到两异面直线的方向向量,借助方向向量所成角求解.
(2)直线与平面所成的角:要求直线a与平面α所成的角θ,先求这个平面α的法向量n与直线a的方向向量a夹角的余弦cos
或者 -
(1)求点M到直线AC1的距离;(2)求点N到平面MA1C1的距离.规律方法 用向量法求空间距离
(1)点线距离的求法如图,在直线l上任取一点B,取直线l的一个方向向量e,则点A到l的距离为| |·sin< ,e>.
(2)点面距离的求法
如图,n是平面α的一个法向量,AB是平面α的一条斜线,则点B到平面α的距离为 .
(3)两平行平面间距离的求法
把求两平行平面间的距离转化为求点面距.
线面距也可转化为求点面距.题型四 易错辨析1.混淆向量与实数的运算性质致误
【典例4】已知a,b都是非零向量,且向量a+3b与7a-5b垂直,向量a-4b与7a-2b垂直,求向量a,b的夹角.纠错:向量的运算性质与实数不同,若b·(2a-b)=0不一定有b=0或2a-b=0,本题在此处误当作实数运算而导致了错误.2.对所求角与向量夹角的关系不理解致误
【典例5】正方体ABCD-A1B1C1D1中,求二面角A-BD1-C的大小.纠错:用法向量的夹角判断二面角的大小时出现错误,根据法向量的方向可知,二面角为钝角,而不是锐角.真题体验1.(2017·全国Ⅰ卷)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,从而AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD. (2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.2.(2017·全国Ⅱ卷)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D
的余弦值.3.(2017·全国Ⅲ卷)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;解:(1)由题设可得△ABD≌△CBD,从而AD=DC.又△ACD是直角三角形,所以∠ADC=90°.取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.所以∠DOB为二面角D-AC-B的平面角.在Rt△AOB中,BO2+AO2=AB2.又AB=BD,
所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.所以平面ACD⊥平面ABC.(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.4.(2016·山东卷)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;(1)证明:设FC的中点为I,连接GI,HI,
在△CEF中,因为点G,I分别是CE,CF的中点,
所以GI∥EF,又EF∥OB,所以GI∥OB,
在△CFB中,因为H,I分别是FB,CF的中点,
所以HI∥BC,又HI∩GI=I,所以平面GHI∥平面ABC,
因为GH?平面GHI,所以GH∥平面ABC.(2)已知EF=FB= AC= ,AB=BC,求二面角F-BC-A的余弦值.谢谢观赏!
