沪教版九年级下数学27.3(2)垂径定理课件(共13张PPT)
文档属性
| 名称 | 沪教版九年级下数学27.3(2)垂径定理课件(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 20:25:58 | ||
图片预览


文档简介
(共13张PPT)
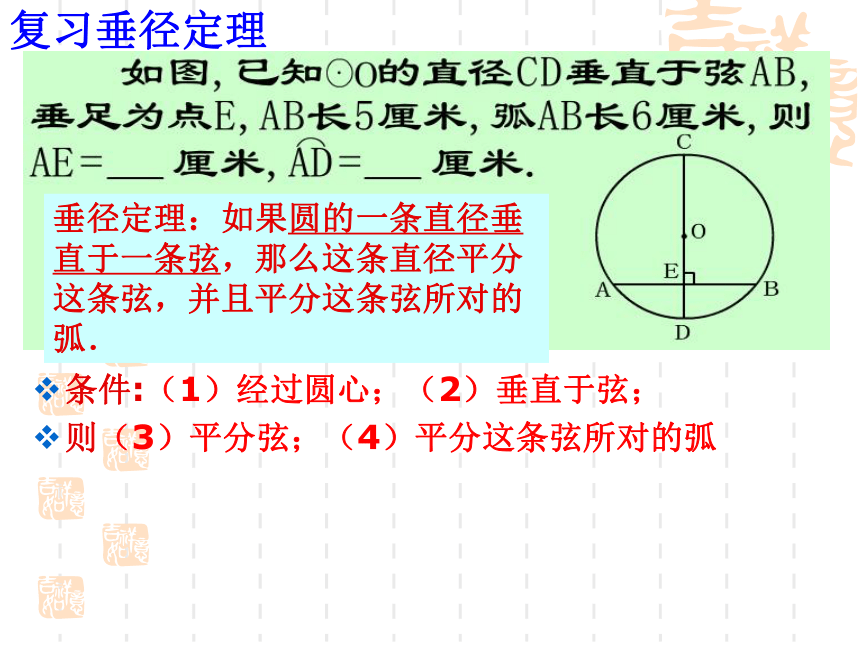
复习垂径定理
垂径定理:如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧.
条件:(1)经过圆心;(2)垂直于弦;
则(3)平分弦;(4)平分这条弦所对的弧
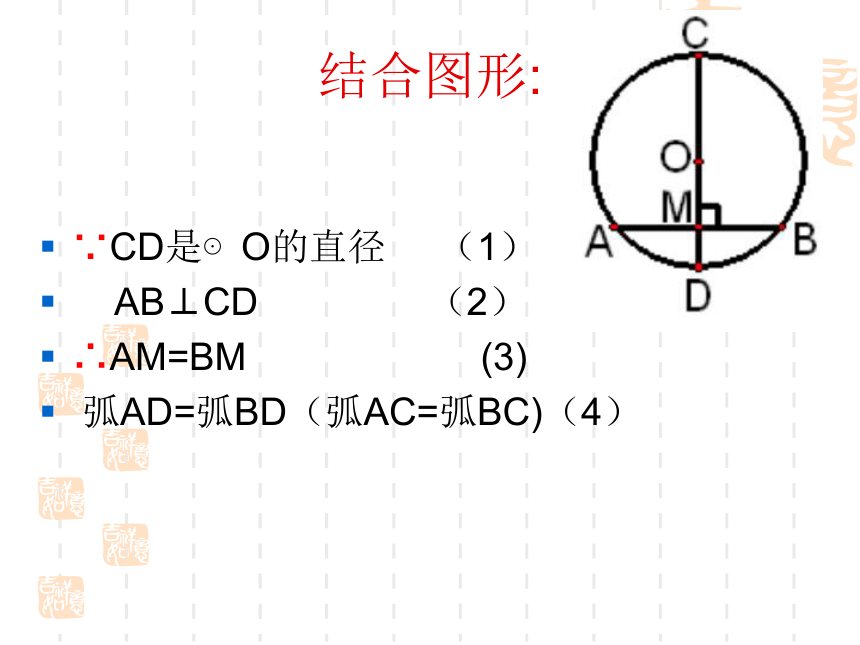
结合图形:
∵CD是⊙O的直径 (1)
AB⊥CD (2)
∴AM=BM (3)
弧AD=弧BD(弧AC=弧BC)(4)
问题1
如图,CD是⊙O的直径,AB是弦(不是直径),CD与AB交于点M.
(1)如果AM=BM,那么CD与AB垂直吗?
·
C
D
A
B
M
如果弦AB是直径,(1)中的结论还成立吗?
O
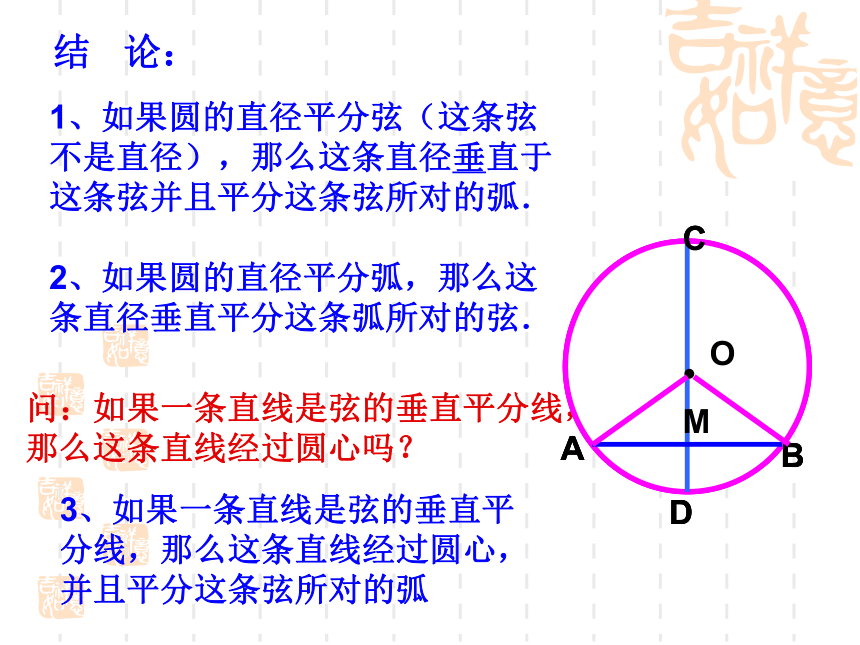
结 论:
3、如果一条直线是弦的垂直平分线,那么这条直线经过圆心,并且平分这条弦所对的弧
问:如果一条直线是弦的垂直平分线,
那么这条直线经过圆心吗?
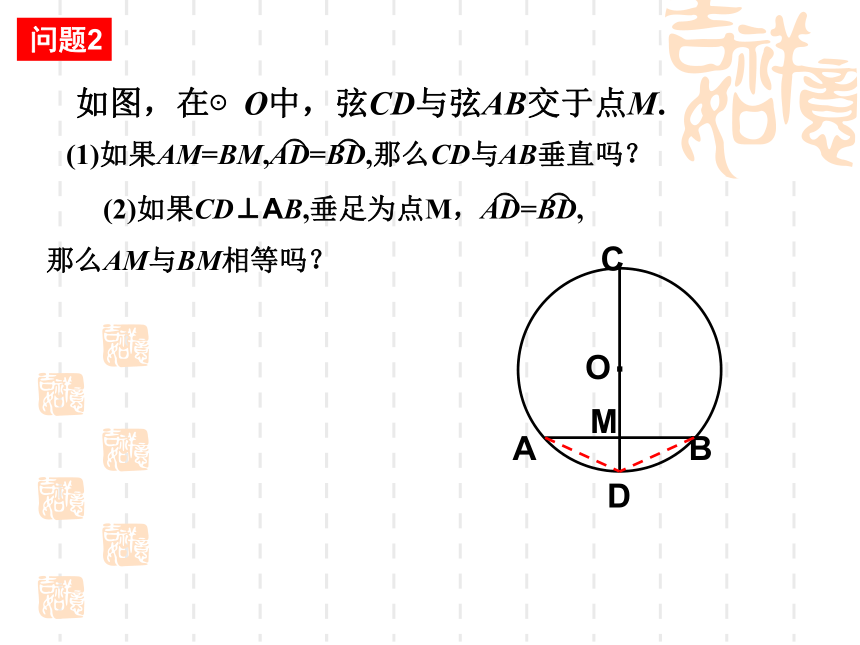
问题2
如图,在⊙O中,弦CD与弦AB交于点M.
经过圆心、垂直于弦、
平分弦、平分弦所对的弧,
这四组关系中,如果有
两组关系成立,那么
其余两组关系也成立。
2、如果一条直线垂直于弦,并且平分弦所对的弧,那么这条直线经过圆心,并且平分这条弦
注:当条件为“直线经过圆心”、
“平分弦”时还要指出这条弦
不是直径,才能推出其余
两组关系也成立!!!
例题1:填空:如图,在⊙O中
(1)若MN⊥AB,MN为直径;则
( ),( ),( );
(2)若AC=BC,MN为直径;AB不是直径,则
( ),( ),( );
(3)若MN⊥AB,AC=BC,则
( ),( ),( );
(4)若弧AM=弧BM,MN为直径,则
( ),( ),( )。
C
O
A
B
D
的长。
求
,
于点
交弦
的中点,
是
中,
⊙
已知
OA
AD
AOB
D
AB
OC
C
O
,
8
120
,
=
°
=
?
例题3 :已知AB,用直尺和圆规平分这条弧.
(
作法
1.联结AB.
2.作线段AB的垂直平分线MN,垂足为C,MN交AB于点D.
AB被点D平分.
A
B
M
N
C
D
(
(
判断:
(1)平分弦的直径,平分这条弦所对的弧。
(2)平分弦的直线,必定过圆心。
(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。
(4)弦的垂直平分线一定是圆的直径。
(5)平分弧的直线,平分这条弧所对的 弦。
(6)弦垂直于直径,这条直径就被弦平分。
(7)平分弦的直径垂直于弦
小结
作业
复习垂径定理
垂径定理:如果圆的一条直径垂直于一条弦,那么这条直径平分这条弦,并且平分这条弦所对的弧.
条件:(1)经过圆心;(2)垂直于弦;
则(3)平分弦;(4)平分这条弦所对的弧
结合图形:
∵CD是⊙O的直径 (1)
AB⊥CD (2)
∴AM=BM (3)
弧AD=弧BD(弧AC=弧BC)(4)
问题1
如图,CD是⊙O的直径,AB是弦(不是直径),CD与AB交于点M.
(1)如果AM=BM,那么CD与AB垂直吗?
·
C
D
A
B
M
如果弦AB是直径,(1)中的结论还成立吗?
O
结 论:
3、如果一条直线是弦的垂直平分线,那么这条直线经过圆心,并且平分这条弦所对的弧
问:如果一条直线是弦的垂直平分线,
那么这条直线经过圆心吗?
问题2
如图,在⊙O中,弦CD与弦AB交于点M.
经过圆心、垂直于弦、
平分弦、平分弦所对的弧,
这四组关系中,如果有
两组关系成立,那么
其余两组关系也成立。
2、如果一条直线垂直于弦,并且平分弦所对的弧,那么这条直线经过圆心,并且平分这条弦
注:当条件为“直线经过圆心”、
“平分弦”时还要指出这条弦
不是直径,才能推出其余
两组关系也成立!!!
例题1:填空:如图,在⊙O中
(1)若MN⊥AB,MN为直径;则
( ),( ),( );
(2)若AC=BC,MN为直径;AB不是直径,则
( ),( ),( );
(3)若MN⊥AB,AC=BC,则
( ),( ),( );
(4)若弧AM=弧BM,MN为直径,则
( ),( ),( )。
C
O
A
B
D
的长。
求
,
于点
交弦
的中点,
是
中,
⊙
已知
OA
AD
AOB
D
AB
OC
C
O
,
8
120
,
=
°
=
?
例题3 :已知AB,用直尺和圆规平分这条弧.
(
作法
1.联结AB.
2.作线段AB的垂直平分线MN,垂足为C,MN交AB于点D.
AB被点D平分.
A
B
M
N
C
D
(
(
判断:
(1)平分弦的直径,平分这条弦所对的弧。
(2)平分弦的直线,必定过圆心。
(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。
(4)弦的垂直平分线一定是圆的直径。
(5)平分弧的直线,平分这条弧所对的 弦。
(6)弦垂直于直径,这条直径就被弦平分。
(7)平分弦的直径垂直于弦
小结
作业
