人教版六年级数学下册 第3单元 圆柱复习课 导学案
文档属性
| 名称 | 人教版六年级数学下册 第3单元 圆柱复习课 导学案 | 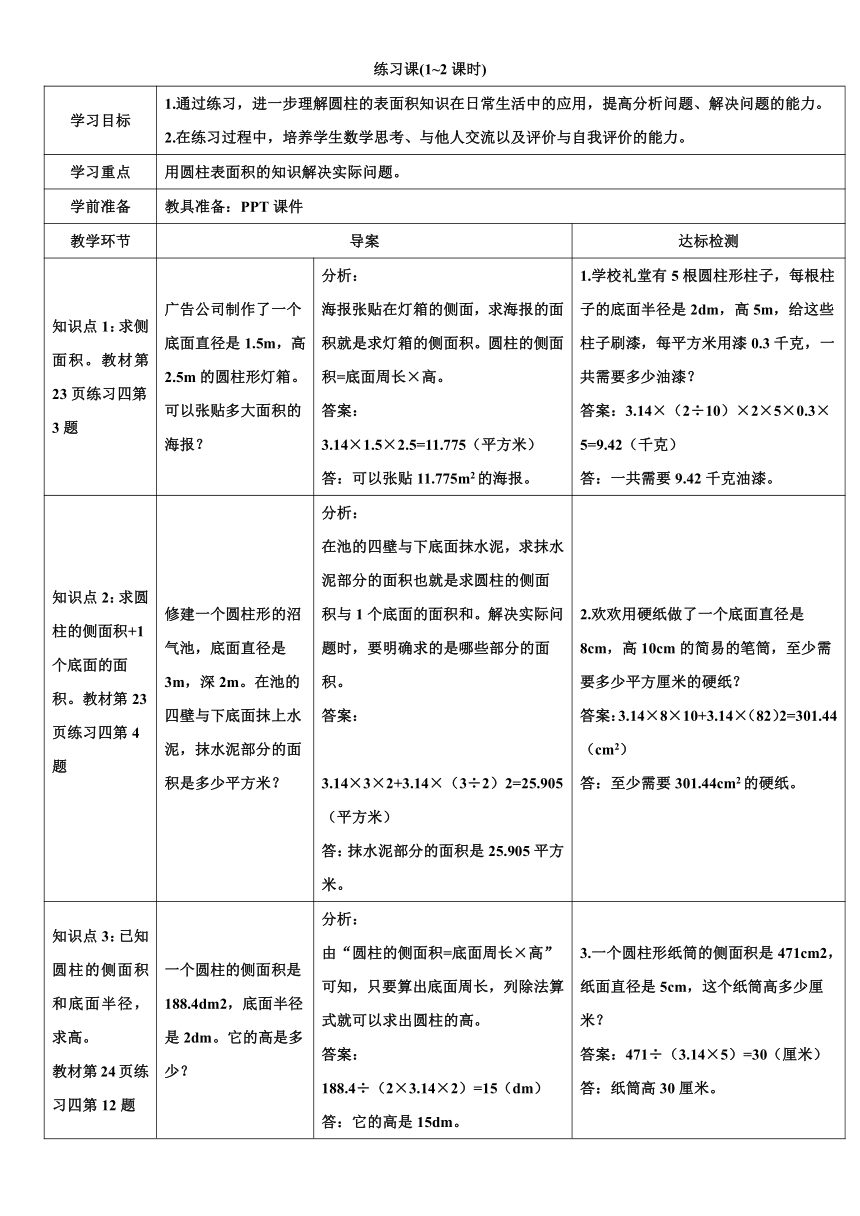 | |
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 21:47:29 | ||
图片预览


文档简介
练习课(1~2课时)
学习目标 1.通过练习,进一步理解圆柱的表面积知识在日常生活中的应用,提高分析问题、解决问题的能力。 2.在练习过程中,培养学生数学思考、与他人交流以及评价与自我评价的能力。
学习重点 用圆柱表面积的知识解决实际问题。
学前准备 教具准备:PPT课件
教学环节 导案 达标检测
知识点1:求侧面积。教材第23页练习四第3题 广告公司制作了一个底面直径是1.5m,高2.5m的圆柱形灯箱。可以张贴多大面积的海报? 分析: 海报张贴在灯箱的侧面,求海报的面积就是求灯箱的侧面积。圆柱的侧面积=底面周长×高。 答案: 3.14×1.5×2.5=11.775(平方米) 答:可以张贴11.775m2的海报。 1.学校礼堂有5根圆柱形柱子,每根柱子的底面半径是2dm,高5m,给这些柱子刷漆,每平方米用漆0.3千克,一共需要多少油漆? 答案:3.14×(2÷10)×2×5×0.3×5=9.42(千克) 答:一共需要9.42千克油漆。
知识点2:求圆柱的侧面积+1个底面的面积。教材第23页练习四第4题 修建一个圆柱形的沼气池,底面直径是3m,深2m。在池的四壁与下底面抹上水泥,抹水泥部分的面积是多少平方米? 分析: 在池的四壁与下底面抹水泥,求抹水泥部分的面积也就是求圆柱的侧面积与1个底面的面积和。解决实际问题时,要明确求的是哪些部分的面积。 答案: 3.14×3×2+3.14×(3÷2)2=25.905(平方米) 答:抹水泥部分的面积是25.905平方米。 2.欢欢用硬纸做了一个底面直径是8cm,高10cm的简易的笔筒,至少需要多少平方厘米的硬纸? 答案:3.14×8×10+3.14×(82)2=301.44(cm2) 答:至少需要301.44cm2的硬纸。
知识点3:已知圆柱的侧面积和底面半径,求高。 教材第24页练习四第12题 一个圆柱的侧面积是188.4dm2,底面半径是2dm。它的高是多少? 分析: 由“圆柱的侧面积=底面周长×高”可知,只要算出底面周长,列除法算式就可以求出圆柱的高。 答案: 188.4÷(2×3.14×2)=15(dm) 答:它的高是15dm。 3.一个圆柱形纸筒的侧面积是471cm2,纸面直径是5cm,这个纸筒高多少厘米? 答案:471÷(3.14×5)=30(厘米) 答:纸筒高30厘米。
知识点4:求组合图形的表面积。 教材第24页练习四第11题第(1)小问 要将路灯柱(如下图)漆上白色的油漆,要漆多少平方米? 分析: 刷油漆部分的面积并不是长方体和圆柱体的表面积之和,长方体的下底面要去掉一个圆,而圆柱体只有侧面才需要刷油漆。 答案: 12×16×3+12×12×2+16×12-3.14×+3.14×12×55=3015.36(平方厘米)=0.301536(平方米) 答:要漆0.301536平方米。 4.工人师傅要在一个零件(如右图)的表面涂一层防锈材料,这个零件上涂防锈材料的面积是多少? 答案:3.14×(6÷2)2×2+3.14×4×2+3.14×6×5=175.84(cm2) 答:这个零件上涂防锈材料的面积是175.84cm2。
知识点5:圆柱被截后表面积的变化。 教材第24页练习四第13题 一根圆柱形木料的底面半径是0.3m,长是2m。如图所示,将它截成4段,这些木料的表面积比原木料增加了多少平方米? 分析: 圆柱被截成4段后,侧面积不变,只是增加了6个底面的面积。 答案: 3.14×0.32×6=1.6956(m2) 答:这些木料的表面积比原木料增加了1.6956m2。 5.把一个底面周长是37.68cm,高是10cm的圆柱,沿底面直径切割后,表面积比原来圆柱的表面积增加了多少平方厘米? 答案:37.68÷3.14×10×2=240(cm2) 答:表面积比原来圆柱的表面积增加了240cm2。
布置作业 1.完成教材第23页5、7题。 2.完成教材第24页8、9、10题。 教学过程中老师的疑问:
课堂总结 1.说一说本节课的收获。 2.谈谈在解决实际问题中有哪些需要注意或不太懂的地方。 1.说一说本节课的收获。 2.自由谈一谈。
教学反思 本节课对本单元圆柱的知识进行了整理和复习。在与学生共同完成单元知识的梳理后(通过边练习边整理的方式),我趁热打铁,安排适当的练习,加深了学生对知识的巩固与理解。在进行练习时,我要求学生一定要先审题,然后解答,这样有利于学生更好地掌握所学的知识。
教师点评和总结:
练习课(3~4课时)
学习目标 1.掌握圆柱体积的计算公式,会运用公式计算圆柱体积。 2.会运用圆柱的体积公式解决有关的简单实际问题。
学习重点 运用圆柱的体积公式解决有关的简单实际问题。
学前准备 教具准备:PPT课件 学具准备:计算器
教学环节 导案 达标检测
知识点1: 已知圆柱的底面半径和高,求圆柱的体积。 教材第28页练习五第5题 一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能装多少吨玉米? 分析:要解决这个问题,先要计算这个粮囤的容积。容积的计算方法与体积的计算方法相同。由公式V=πr2h可直接计算出粮囤的容积。 答案:3.14×1.52×2×750=10597.5(千克)=10.5975(吨) 答:这个粮囤能装10.5975吨玉米。 1.一个圆柱形汽油桶,从里面量底面半径5分米,深1.5米,这个汽油桶最多能装多少升汽油? 答案:3.14×52×1.5×10=1177.5(立方分米)=1177.5(升) 答:这个汽油桶最多能装1177.5升汽油。
知识点2:已知圆柱的底面直径和高,求圆柱的体积。 教材第28页练习五第3题 学校新建了两个同样大小的圆柱形花坛。花坛的底面内直径为3m,高为0.8m。如果里面填土的高度是0.5m,两个花坛中共需要填土多少立方米? 分析:填土的部分是圆柱形,该题实际是求底面直径为3m,高为0.5m的两个圆柱的体积。根据公式V=πh直接计算可得。 答案:3.14××0.5=3.5325(m3) 3.5325×2=7.065(m3) 答:两个花坛中共需要填土7.065立方米。 2.一段圆柱形实心钢材,长是80厘米,横截面直径是10厘米。每立方厘米钢材重7.8克,这段钢材重多少千克?(得数保留一位小数) 答案:3.14××80×7.8÷1000=48.984(千克)≈49.0(千克) 答:这段钢材重49.0千克。
知识点3:已知圆柱的体积和底面积,求高。 教材第28页练习五第4题 一个圆柱的体积是80cm3,底面积是16cm2。它的高是多少厘米? 分析:由圆柱的体积公式V=Sh可得h=,由此公式可直接算出圆柱的高。 答案:80÷16=5(cm) 答:圆柱的高是5厘米。 3.小明将4710毫升的牛奶倒入一个圆柱形的玻璃容器中,这个容器的底面半径是10厘米,高20厘米。可以装多深? 答案:4710÷(3.14×102)=15(cm) 答:可以装15厘米。
知识点4:两个圆柱中,高、底面积和体积三个量有一个量相等,求其余的量。教材第29页练习五第9题 两个底面积相等的圆柱,一个高为4.5dm,体积为81dm3。另一个高为3dm,它的体积是多少? 分析:由公式S=可以把圆柱的底面积求出来,根据底面积相等,由V=Sh可以把另一个圆柱的体积计算出来。 答案:81÷4.5×3=54(dm3) 答:它的体积是54dm3。 4.两个高相等的圆柱,一个底面积是25cm2,体积是100cm3。另一个底面积是28cm2,它的体积是多少? 答案:100÷25×28=112(cm3) 答:它的体积是112cm3。
知识点5:把其它形状物体的体积转化成等量的圆柱的体积解决问题。教材第29页练习五第10题 一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少? 分析:无论铁块放在水中还是取出来,铁块的体积不变,铁块的体积也就是取出铁块后下降的这部分水的体积。 答案:3.14×()2×2=157(cm3) 答:这块铁块的体积是157cm3。 5.小立在一个底面直径是20cm(从里面量)的圆柱形鱼缸里放了一块石头(石头完全浸没在水中),水面由30cm上升到34cm,这块石头的体积是多少? 答案:3.14×(20÷2)2×(34-30)=1256(cm3) 答:这块石头的体积是1256cm3。
知识点6:空心圆柱体体积的计算方法。教材第29页练习五第12题 下面是一根钢管,求它所用钢材的体积。(单位:cm) 分析:求空心圆柱的体积就是用大圆柱的体积减去小圆柱的体积。 答案:3.14×[()2-()2]×80=2260.8(cm3) 答:它所用钢材的体积是2260.8cm3。 6.求下图钢管的体积。(单位:dm) 答案:3.14×[( )2-(2]×8=9.0432(dm3) 答:钢管的体积是9.0432dm3。
布置作业 1.完成教材第28页第6题。 2.完成教材第29页第7、11、13题。 教学过程中老师的疑问:
课堂总结 1.说一说本节课的收获。 2.谈谈在解决实际问题中有哪些需要注意或不太懂的地方。 1.说一说本节课的收获。 2.自由谈一谈。
教学反思 本节课的教学主要是如何灵活地运用圆柱的体积公式,教学中由易到难,循序渐进,教师要引导学生理解并会运用圆柱体积公式解决基础及稍复杂的实际问题。
教师点评和总结:
PAGE
