人教版九年级数学下册: 27.2.1 相似三角形的判定公开课 课件(共26张PPT)
文档属性
| 名称 | 人教版九年级数学下册: 27.2.1 相似三角形的判定公开课 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 22:20:02 | ||
图片预览



文档简介
(共24张PPT)
27.2.1相似三角形的判定(1)
学习目标:
1.了解三角形相似是概念。
2.理解平行线分线段成比例的基本事实.
A′
B′
C′
10
6
12
51°
82°
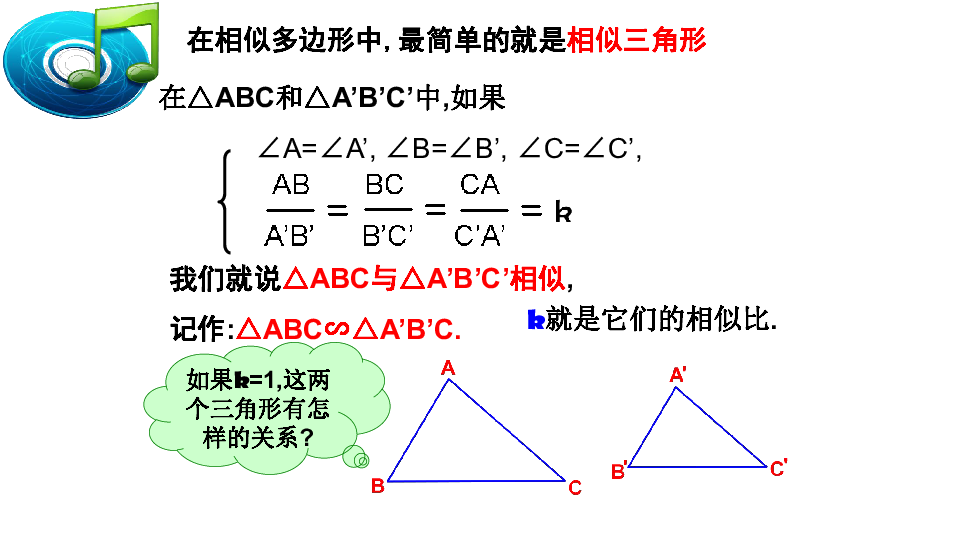
它们是相似三角形吗?为什么?
A
6
B
C
5
3
82°
47°
6
回顾
在相似多边形中,最简单的就是相似三角形
在△ABC和△A’B’C’中,如果
∠A=∠A’, ∠B=∠B’, ∠C=∠C’,
我们就说△ABC与△A’B’C’相似,
记作:△ABC∽△A’B’C.
k就是它们的相似比.
如果k=1,这两个三角形有怎样的关系?
如图,任意画两条直线l1,l2,再画三条与l1,l2都相交的平行线l3,l4,l5,分别度量l3,l4,l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,
与 相等吗 ?任意平移l4, 与 还相等吗?你还能发现哪些成比例线段?
平行线分线段成比例定理:三条______
截两条直线,所得的_____线段的比_____.
平行线分线段
成比例定理
对应
相等
平行线
把直线l2向左平移,两直线相交时,有两种特殊的交点,图(1)是把l4看成平行于△ACF的边CF的直线;图(2)是把l3看成平行于△FBC边CF的直线,那么我们能得出什么结论呢?
如果将平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况,如下图所示:
思维表征
平行于三角形一边的直线截其他两边(或两边延长线),所得的_______线段的比______.
注:用这个结论可以证明三角形中的对应线段的比______
对应
相等
相等
平行线分线段成比例定理推论
如图,在△ABC中,点D是边AB上的点,DE//BC,DE交AC于点E, △ADE与△ABC有什么关系?
思
考
?
直觉告诉我们, △ADE与△ABC相似,我们通过相似的定义证明这个结论.
先证明两个三角形的对应角相等.
在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
四边形BFED平行四边形,
DE//BC, EF//AB.
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似.
△ADE∽△ABC
改变点D在AB上的位置,继续观察图形,容易进一步猜想△AD’E’与△ABC仍有相似关系.因此,我们有:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。
D
E
A
C
B
即:
如果DE∥BC,
那么△ADE∽△ABC
你能证明吗?
X型
延伸
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。
D
E
A
C
B
延伸
即:
如果DE∥BC,
那么△ADE∽△ABC
你能证明吗?
X型
X型
延伸
平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
理解
思维迁移
1、如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形(C)
A、1对 B、2对
C、3对 D、4对
练一练
思维迁移
2、如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.
则AD的长为 ( )
(A) (B)2
(C)3 (D)
D
6
3、如图,△ABC中,DE∥BC,
若 , DE=2,则BC= .
练一练
4.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
运用
5.已知:如图,AB∥EF ∥CD,
3
图中共有____对相似三角形。
△EOF∽△COD
AB∥EF
△AOB∽ △FOE
AB∥CD
EF∥CD
△AOB ∽△DOC
理解
A.7 B.7.5 C.8 D.8.5
6.如图,直线a//b//c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF=( ).
B
思维迁移
7、如图△ABC∽△DCA,AD∥BC,∠B=∠DCA.
(1)写出对应边的比例式;
(2)写出所有相等的角;
(3)若AB=10,BC=12,CA=6.
求AD、DC的长.
解:(1)
(2)∠BAC=∠CDA,∠B=∠DCA,∠ACB=∠DAC;
(3)∵
又AB=10,BC=12,CA=6
思维迁移
8、已知:梯形ABCD中,AD∥BC,EF∥BC,AE=FC,
,
,求:AE的长.
解:∵AD∥BC,EF∥BC
∴AD∥EF∥BC
又∵AE=FC
∴AE=6.
27.2.1相似三角形的判定(1)
学习目标:
1.了解三角形相似是概念。
2.理解平行线分线段成比例的基本事实.
A′
B′
C′
10
6
12
51°
82°
它们是相似三角形吗?为什么?
A
6
B
C
5
3
82°
47°
6
回顾
在相似多边形中,最简单的就是相似三角形
在△ABC和△A’B’C’中,如果
∠A=∠A’, ∠B=∠B’, ∠C=∠C’,
我们就说△ABC与△A’B’C’相似,
记作:△ABC∽△A’B’C.
k就是它们的相似比.
如果k=1,这两个三角形有怎样的关系?
如图,任意画两条直线l1,l2,再画三条与l1,l2都相交的平行线l3,l4,l5,分别度量l3,l4,l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,
与 相等吗 ?任意平移l4, 与 还相等吗?你还能发现哪些成比例线段?
平行线分线段成比例定理:三条______
截两条直线,所得的_____线段的比_____.
平行线分线段
成比例定理
对应
相等
平行线
把直线l2向左平移,两直线相交时,有两种特殊的交点,图(1)是把l4看成平行于△ACF的边CF的直线;图(2)是把l3看成平行于△FBC边CF的直线,那么我们能得出什么结论呢?
如果将平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况,如下图所示:
思维表征
平行于三角形一边的直线截其他两边(或两边延长线),所得的_______线段的比______.
注:用这个结论可以证明三角形中的对应线段的比______
对应
相等
相等
平行线分线段成比例定理推论
如图,在△ABC中,点D是边AB上的点,DE//BC,DE交AC于点E, △ADE与△ABC有什么关系?
思
考
?
直觉告诉我们, △ADE与△ABC相似,我们通过相似的定义证明这个结论.
先证明两个三角形的对应角相等.
在△ADE与△ABC中, ∠A=∠A,
∵DE//BC,
∴∠ADE=∠B, ∠AED=∠C.
再证明两个三角形的对应边的比相等.
过E作EF//AB,EF交BC于F点.
四边形BFED平行四边形,
DE//BC, EF//AB.
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B, ∠AED=∠C.
这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似.
△ADE∽△ABC
改变点D在AB上的位置,继续观察图形,容易进一步猜想△AD’E’与△ABC仍有相似关系.因此,我们有:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。
D
E
A
C
B
即:
如果DE∥BC,
那么△ADE∽△ABC
你能证明吗?
X型
延伸
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似。
D
E
A
C
B
延伸
即:
如果DE∥BC,
那么△ADE∽△ABC
你能证明吗?
X型
X型
延伸
平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
理解
思维迁移
1、如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形(C)
A、1对 B、2对
C、3对 D、4对
练一练
思维迁移
2、如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.
则AD的长为 ( )
(A) (B)2
(C)3 (D)
D
6
3、如图,△ABC中,DE∥BC,
若 , DE=2,则BC= .
练一练
4.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____。
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
运用
5.已知:如图,AB∥EF ∥CD,
3
图中共有____对相似三角形。
△EOF∽△COD
AB∥EF
△AOB∽ △FOE
AB∥CD
EF∥CD
△AOB ∽△DOC
理解
A.7 B.7.5 C.8 D.8.5
6.如图,直线a//b//c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF=( ).
B
思维迁移
7、如图△ABC∽△DCA,AD∥BC,∠B=∠DCA.
(1)写出对应边的比例式;
(2)写出所有相等的角;
(3)若AB=10,BC=12,CA=6.
求AD、DC的长.
解:(1)
(2)∠BAC=∠CDA,∠B=∠DCA,∠ACB=∠DAC;
(3)∵
又AB=10,BC=12,CA=6
思维迁移
8、已知:梯形ABCD中,AD∥BC,EF∥BC,AE=FC,
,
,求:AE的长.
解:∵AD∥BC,EF∥BC
∴AD∥EF∥BC
又∵AE=FC
∴AE=6.
