沪科版安徽省蚌埠市2019-2020学年第一学期期末考试九年级数学试卷(图片版,含答案)
文档属性
| 名称 | 沪科版安徽省蚌埠市2019-2020学年第一学期期末考试九年级数学试卷(图片版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 686.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 00:00:00 | ||
图片预览


文档简介
书
蚌埠市2019—2020学年度第一学期期末教学质量监测
九年级数学(沪科版)
考试时间:120分钟 满分:150分
一、选择题:(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符
合题意的,请在答题卷上将正确答案的字母代号涂黑)
1?计算:2sin30°=
槡 槡A?1 B?3 C?2 D?23
2?若双曲线y=k-1x的图象的一支位于第三象限,则k的取值范围是
A?k<1 B?k>1 C?0<k<1 D?k≤1
3?抛物线y=(x-3)2-2经过平移得到抛物线y=x2,平移过程正确的是
A?先向下平移2个单位,再向左平移3个单位
B?先向上平移2个单位,再向右平移3个单位
C?先向下平移2个单位,再向右平移3个单位
D?先向上平移2个单位,再向左平移3个单位
4?若△ABC与△A1B1C1相似且对应中线之比为2∶5,则周长之比和面积比分别是
A?2∶5,4∶5 B?2∶5,4∶25 C?4∶25,4∶25 D?4∶25,2∶5
5?关于二次函数y=2x2+4x-1,下列说法正确的是
A?图象与y轴的交点坐标为(0,1) B?y的最小值为-3
C?当x<0时,y随x的增大而减小 D?图象的对称轴在y轴的右侧
6?已知某函数的图象P与函数y=-2x的图象关于直线x=2对称,则以下各点一定在图象P
上的是
A?(2,-1) B?(1,-2) C?(0,-1) D?(2,-1)
7?已知二次函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是
A?k>-74 B?k≥-
7
4 C?k≥-
7
4且k≠0 D?k>-
7
4且k≠0
8?如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正切值为
A?2 B? 槡255 C?
槡5
5 D?
1
2
第8题图 第9题图 第10题图
)页4共(页1第卷试学数级年九市埠蚌
9?已知抛物线y=14x
2+1具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到 x轴
的距离相等.如图点M的坐标为(3,6),P是抛物线y=14x
2+1上一动点,则△PMF周长的
最小值是
A?5 B?9 C?11 D?1
10?如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分
割点(AP2<P1P2),点 P3是线段 AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段
AP2020的长度是
A? 槡3-5( )2
2020
B?槡5-1( )2
2020
C?( )12
2020
D?槡( )5-2
1010
二、填空题:(本大题共4个小题,每小题5分,共20分,请将答案直接填在题中的横线上)
11?已知a6=
b
5=
c
4,且a+b-2c=6,则a的值为 ?
12?如图,一次函数y1=ax+b和反比例函数y2=
k
x的图象相交于A,B两点,则使y1>y2成立
的x取值范围是 ?
13?如图,正方形ABCD的对角线 AC上有一点 E,且 CE=4AE,点 F在 DC的延长线上,连接
EF,过点E作 EG⊥EF,交 CB的延长线于点 G,若 AB=5,CF=2,则线段 BG的长是
?
14?如图,在矩形ABCD中,E在AB上,在矩形ABCD的内部作正方形BEFG?当AB=6,BC=8
时,若直线AF将矩形ABCD的面积分成1∶3两部分,则BE的长为 ?
第12题图 第13题图 第14题图
三、(本题共两小题,每小题8分,共16分)
15?计算:2cos30°-tan45°- (1-tan60°)槡
2?
16?在锐角三角形ABC中,已知AB=8,AC=10,△ABC的面积为 槡203,求∠A的余弦值?
)页4共(页2第卷试学数级年九市埠蚌
第17题图
四、(本题共两小题,每小题8分,共16分)
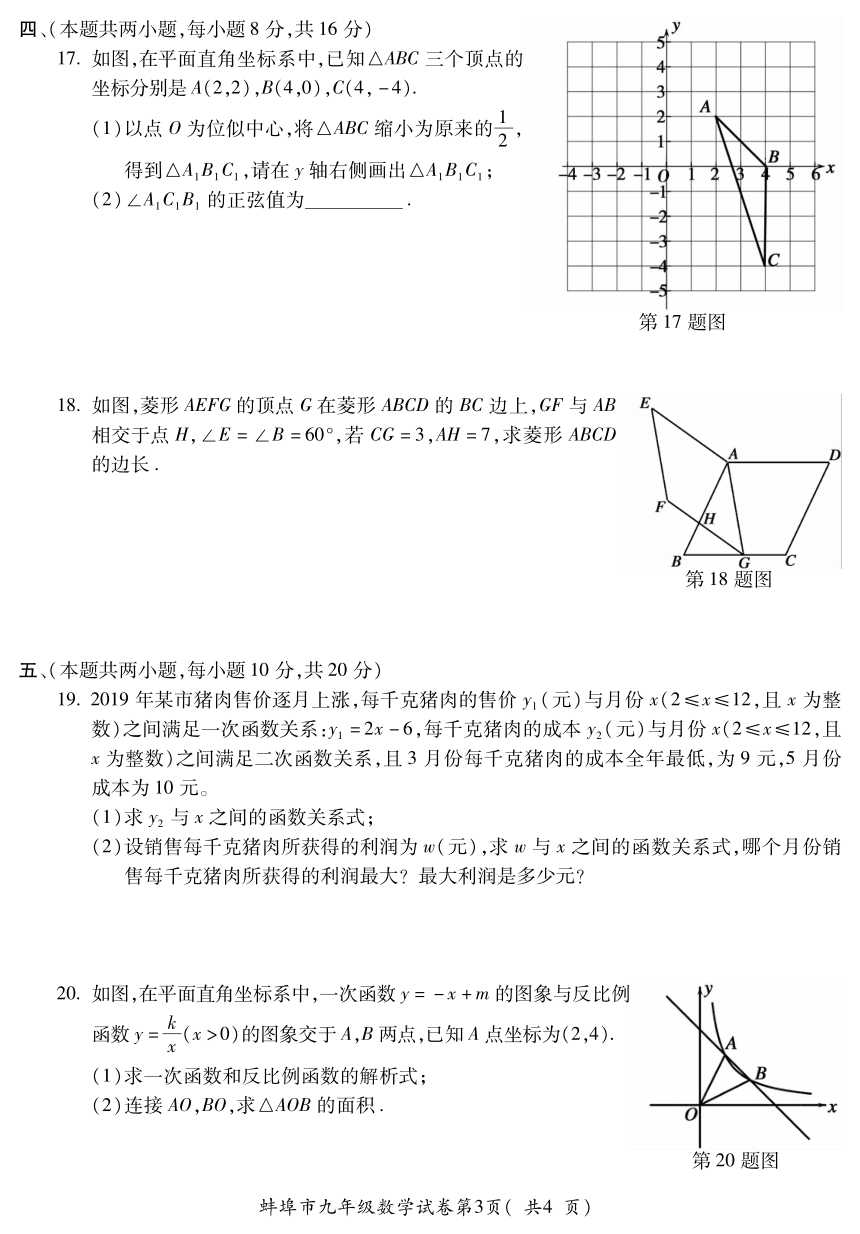
17?如图,在平面直角坐标系中,已知△ABC三个顶点的
坐标分别是A(2,2),B(4,0),C(4,-4).
(1)以点O为位似中心,将△ABC缩小为原来的12,
得到△A1B1C1,请在y轴右侧画出△A1B1C1;
(2)∠A1C1B1的正弦值为 ?
第18题图
18?如图,菱形AEFG的顶点G在菱形ABCD的BC边上,GF与 AB
相交于点H,∠E=∠B=60°,若 CG=3,AH=7,求菱形 ABCD
的边长?
五、(本题共两小题,每小题10分,共20分)
19?2019年某市猪肉售价逐月上涨,每千克猪肉的售价 y1(元)与月份 x(2≤x≤12,且 x为整
数)之间满足一次函数关系:y1=2x-6,每千克猪肉的成本y2(元)与月份x(2≤x≤12,且
x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,5月份
成本为10元。
(1)求y2与x之间的函数关系式;
(2)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销
售每千克猪肉所获得的利润最大?最大利润是多少元?
第20题图
20?如图,在平面直角坐标系中,一次函数y=-x+m的图象与反比例
函数y=kx(x>0)的图象交于A,B两点,已知A点坐标为(2,4).
(1)求一次函数和反比例函数的解析式;
(2)连接AO,BO,求△AOB的面积?
)页4共(页3第卷试学数级年九市埠蚌
六、(本题满分12分)
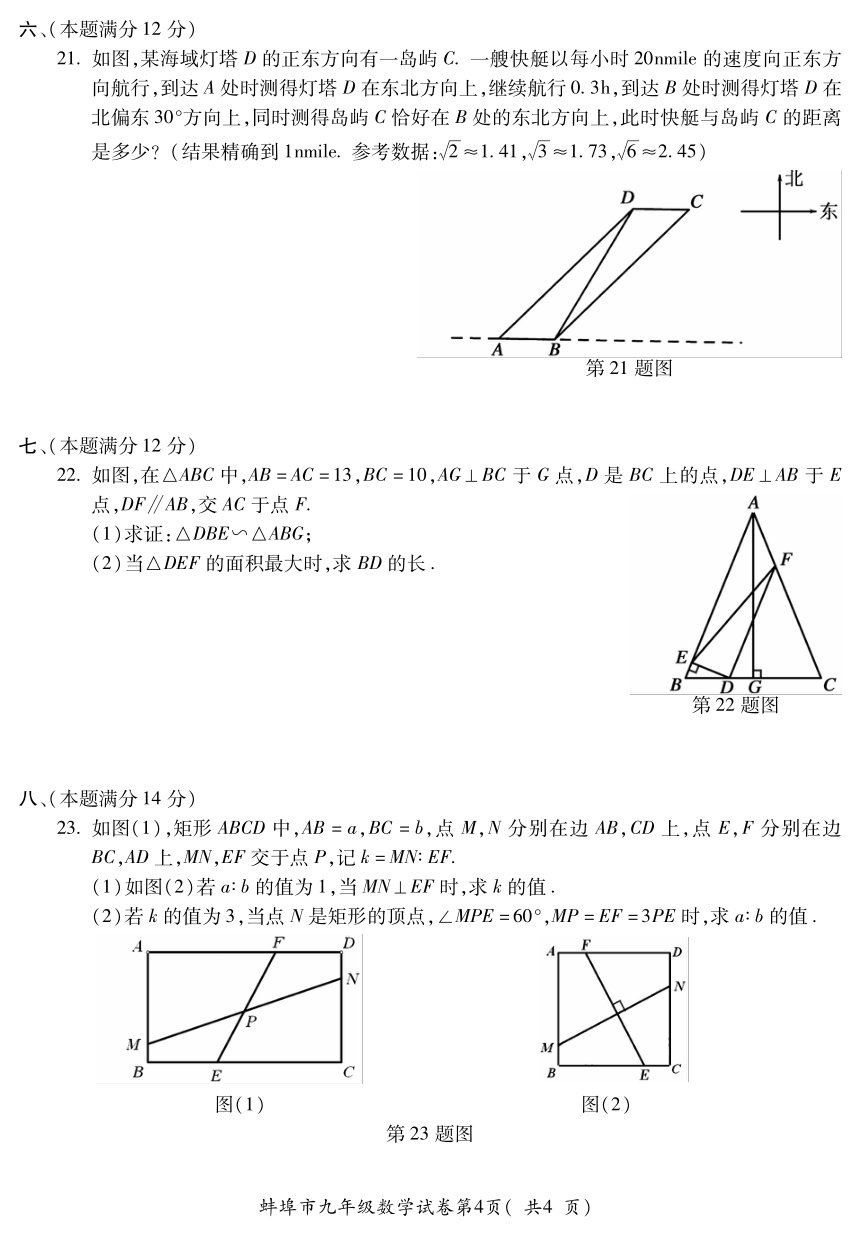
21?如图,某海域灯塔D的正东方向有一岛屿C?一艘快艇以每小时20nmile的速度向正东方
向航行,到达A处时测得灯塔D在东北方向上,继续航行0?3h,到达B处时测得灯塔D在
北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离
是多少?(结果精确到1nmile?参考数据:槡2≈1?41,槡3≈1?73,槡6≈2?45)
第21题图
七、(本题满分12分)
22?如图,在△ABC中,AB=AC=13,BC=10,AG⊥BC于 G点,D是 BC上的点,DE⊥AB于 E
第22题图
点,DF∥AB,交AC于点F?
(1)求证:△DBE∽△ABG;
(2)当△DEF的面积最大时,求BD的长?
八、(本题满分14分)
23?如图(1),矩形 ABCD中,AB=a,BC=b,点 M,N分别在边 AB,CD上,点 E,F分别在边
BC,AD上,MN,EF交于点P,记k=MN∶EF?
(1)如图(2)若a∶b的值为1,当MN⊥EF时,求k的值?
(2)若k的值为3,当点N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a∶b的值?
图(1) 图(2)
第23题图
)页4共(页4第卷试学数级年九市埠蚌
蚌埠市2019—2020学年度第一学期期末教学质量监测
九年级数学参考答案和评分标准(沪科版)
一、选择题:(本大题共10小题,每小题4分,共40分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 A B D B B A C D C A
二、填空题:(本大题共4个小题,每小题5分,共20分)
11?12 12?x<-2或0<x<4 13?5 14?125或
48
11
三、本题共两小题,每小题8分,共16分
15?解:原式=2×槡32 槡-1-|1-3| 4分…………………………………………………………
=0. 8分………………………………………………………………………………
16?解:过B点作BD⊥AC于点D,由三角形面积公式可求得BD 槡=43, 3分…………………
由勾股定理得AD=4, 6分…………………………………………………………………
所以cosA=12. 8分………………………………………………………………………
四、本题共两小题,每小题8分共16分
17?解:(1)以点O为位似中心,将△ABC缩小为原来的
1
2,得到△A1B1C1,请在y轴右侧画出△A1B1C1;
4分…………………………………………
(2)槡1010? 8分…………………………………
18?解:连接AC?
∵∠B=60°,AB=BC,
∴△ABC是等边三角形, 2分…………………
设AB=BC=AC=a,则BH=a-7,BG=a-3,
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,
∵∠AGH=∠ACG=60°,∴∠BGH=∠CAG,
∵∠B=∠ACG,∴△BGH∽△CAG, 5分……………
∴BGAC=
BH
CG,∴
a-3
a =
a-7
3 ,
∴a2-10a+9=0,∴a=9或a=1(舍),
∴AB=9. 8分…………………………………………
)页4共(页1第 准标分评和案答考参卷试学数级年九市埠蚌
19?(本题满分10分)
解:(1)由题意得,抛物线的顶点坐标为(3,9),且经过(5,10).
设y2与x之间的函数关系式为:y2=a(x-3)
2+9, 2分……………………………
将(5,10)代入y2=a(x-3)
2+9得a(5-3)2+9=10,
解得:a=14,
∴y2=
1
4(x-3)
2+9=14x
2-32x+
45
4. 5分…………………………………………
(2)由题意得,
w=y1-y2=2x+6-(
1
4x
2-32x+
45
4)
=-14x
2+72x-
21
4=-
1
4(x-7)
2+7。 7分………………………………………
∴当x=7时,w取最大值7?
∴7月份利润最大,最大利润为7元。 10分…………………………………………
20?(本题满分10分)
解:(1)将A(2,4)代入y=-x+m与y=kx(x>0)得4=-2+m,4=
k
2, 2分…………
∴m=6,k=8,
∴一次函数的解析式为y=-x+6,反比例函数的解析式为y=8x; 4分…………
(2)解方程组
y=-x+6,
y=8x
{ . 得 x=2,y=4{ ,或 x=4,y=2{ . ∴B(4,2), 6分………………………
设直线y=-x+6与x轴,y轴交于C,D点,易得D(0,6),即OD=6, 8分………
∴S△AOB=S△DOB-S△AOD=6? 10分……………………………………………………
21?(本题满分12分)
解:过点D作DE⊥AB于点E,过点C作CF⊥AB于
点F,如图所示?
则DE∥CF,∠DEA=∠CFA=90°?
即CDEF为矩形,∴CF=DE?
依题意DC∥EF,AD∥BC,∴四边形CDEF为平行四边形? 4分………………………
根据题意,得:∠DAB=45°,∠DBE=60°,∠CBF=45°?
)页4共(页2第 准标分评和案答考参卷试学数级年九市埠蚌
设DE=x(nmile),则AE=x(nmile)?
在Rt△DEB中,∵tan∠DBE=DEBE 槡=3,∴BE=
槡3
3x(nmile)? 8分……………………
∵AB=AE-BE=20×0?3=6(nmile),
∴x-槡33x=6,解得:x 槡=9+33,
∴CF=DE=( 槡9+33)nmile?
在Rt△CBF中,sin∠CBF=CFBC=
槡2
2,∴BC 槡 槡=92+36≈20(nmile)?
答:此时快艇与岛屿C的距离是20nmile? 12分…………………………………………
22?(本题满分12分)
解:(1)证明:∵DE⊥AB,AG⊥BC,∴∠BED=∠AGB=90°,
∵∠B=∠B,∴△DBE∽△ABG? 4分………………………………………………
(2)解:BC=10,BG=5,AG=12,BD=x,CD=10-x,ED=1213x,
∵DF∥AB,∴DFAB=
CD
CB,
∴DF=1?3(10-x),
∴ΔDEF的面积S=12×
12
13x×1?3(10-x)=0?6x(10-x). 8分…………………
=-0?6(x-5)2+15,
∵当△DEF的面积最大时,x=5,即BD的长为5 12分……………………………
23?(本题满分14分)
解:(1)如图1,作EH⊥BC于H,MQ⊥CD于Q,设EF交MN于点O?
∵四边形ABCD是正方形,∴FH=AB,MQ=BC,
∴AB=CB,∴EH=MQ,
∵EF⊥MN,∴∠EON=90°,
∵∠ECN=90°,∴∠MNQ+∠CEO=180°,∠FEH+∠CEO=180°
∴∠FEH=∠MNQ,∵∠EHF=∠MQN=90°,
∴ΔFHE≌ΔMQN, 4分…………………………………………………………………
∴MN=EF,∴k=MN∶EF=1? 6分…………………………………………………
(2)连接FN,ME?
)页4共(页3第 准标分评和案答考参卷试学数级年九市埠蚌
∵k=3,MP=EF=3PE,∴MNPM=
3EF
3PE=
EF
PE=3,
∴PNPM=
PF
PE=2,又∠FPN=∠EPM,
∴ΔPNF∽ΔPEM,∴NFME=
PN
PM=2,ME∥NF, 9分……………………………………
设PE=2m,则PF=4m,MP=6m,NP=12m,
①如图2,当点N与点D重合时,点M恰好与B重合?作FH⊥BD于H?
∵∠MPE=∠FPH=60°,∴PH=2m,FH 槡=23m,DH=10m,
∴ab=
AB
AD=
FH
HD=
槡3
5? 11分…………………………………………………………
②如图3,当点N与C重合,作EH⊥MN于H?则PH=m,HE 槡=3m,
∴HC=PH+PC=13m,∴tan∠HCE=MBBC=
HE
HC=
槡3
13,
∵ME∥FC,∴∠MEB=∠FCB=∠CFD,
∵∠B=∠D,∴ΔMEB∽ΔCFD,
∴CDMB=
FC
ME=2,∴
a
b=
CD
BD=
2MB
BC=
槡23
13,
综上所述,a∶b的值为槡35或
槡23
13? 14分………………………………………………
图1 图2 图3
(其它解法请根据以上评分标准酌情赋分)
)页4共(页4第 准标分评和案答考参卷试学数级年九市埠蚌
蚌埠市2019—2020学年度第一学期期末教学质量监测
九年级数学(沪科版)
考试时间:120分钟 满分:150分
一、选择题:(本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符
合题意的,请在答题卷上将正确答案的字母代号涂黑)
1?计算:2sin30°=
槡 槡A?1 B?3 C?2 D?23
2?若双曲线y=k-1x的图象的一支位于第三象限,则k的取值范围是
A?k<1 B?k>1 C?0<k<1 D?k≤1
3?抛物线y=(x-3)2-2经过平移得到抛物线y=x2,平移过程正确的是
A?先向下平移2个单位,再向左平移3个单位
B?先向上平移2个单位,再向右平移3个单位
C?先向下平移2个单位,再向右平移3个单位
D?先向上平移2个单位,再向左平移3个单位
4?若△ABC与△A1B1C1相似且对应中线之比为2∶5,则周长之比和面积比分别是
A?2∶5,4∶5 B?2∶5,4∶25 C?4∶25,4∶25 D?4∶25,2∶5
5?关于二次函数y=2x2+4x-1,下列说法正确的是
A?图象与y轴的交点坐标为(0,1) B?y的最小值为-3
C?当x<0时,y随x的增大而减小 D?图象的对称轴在y轴的右侧
6?已知某函数的图象P与函数y=-2x的图象关于直线x=2对称,则以下各点一定在图象P
上的是
A?(2,-1) B?(1,-2) C?(0,-1) D?(2,-1)
7?已知二次函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是
A?k>-74 B?k≥-
7
4 C?k≥-
7
4且k≠0 D?k>-
7
4且k≠0
8?如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正切值为
A?2 B? 槡255 C?
槡5
5 D?
1
2
第8题图 第9题图 第10题图
)页4共(页1第卷试学数级年九市埠蚌
9?已知抛物线y=14x
2+1具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到 x轴
的距离相等.如图点M的坐标为(3,6),P是抛物线y=14x
2+1上一动点,则△PMF周长的
最小值是
A?5 B?9 C?11 D?1
10?如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分
割点(AP2<P1P2),点 P3是线段 AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段
AP2020的长度是
A? 槡3-5( )2
2020
B?槡5-1( )2
2020
C?( )12
2020
D?槡( )5-2
1010
二、填空题:(本大题共4个小题,每小题5分,共20分,请将答案直接填在题中的横线上)
11?已知a6=
b
5=
c
4,且a+b-2c=6,则a的值为 ?
12?如图,一次函数y1=ax+b和反比例函数y2=
k
x的图象相交于A,B两点,则使y1>y2成立
的x取值范围是 ?
13?如图,正方形ABCD的对角线 AC上有一点 E,且 CE=4AE,点 F在 DC的延长线上,连接
EF,过点E作 EG⊥EF,交 CB的延长线于点 G,若 AB=5,CF=2,则线段 BG的长是
?
14?如图,在矩形ABCD中,E在AB上,在矩形ABCD的内部作正方形BEFG?当AB=6,BC=8
时,若直线AF将矩形ABCD的面积分成1∶3两部分,则BE的长为 ?
第12题图 第13题图 第14题图
三、(本题共两小题,每小题8分,共16分)
15?计算:2cos30°-tan45°- (1-tan60°)槡
2?
16?在锐角三角形ABC中,已知AB=8,AC=10,△ABC的面积为 槡203,求∠A的余弦值?
)页4共(页2第卷试学数级年九市埠蚌
第17题图
四、(本题共两小题,每小题8分,共16分)
17?如图,在平面直角坐标系中,已知△ABC三个顶点的
坐标分别是A(2,2),B(4,0),C(4,-4).
(1)以点O为位似中心,将△ABC缩小为原来的12,
得到△A1B1C1,请在y轴右侧画出△A1B1C1;
(2)∠A1C1B1的正弦值为 ?
第18题图
18?如图,菱形AEFG的顶点G在菱形ABCD的BC边上,GF与 AB
相交于点H,∠E=∠B=60°,若 CG=3,AH=7,求菱形 ABCD
的边长?
五、(本题共两小题,每小题10分,共20分)
19?2019年某市猪肉售价逐月上涨,每千克猪肉的售价 y1(元)与月份 x(2≤x≤12,且 x为整
数)之间满足一次函数关系:y1=2x-6,每千克猪肉的成本y2(元)与月份x(2≤x≤12,且
x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,5月份
成本为10元。
(1)求y2与x之间的函数关系式;
(2)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销
售每千克猪肉所获得的利润最大?最大利润是多少元?
第20题图
20?如图,在平面直角坐标系中,一次函数y=-x+m的图象与反比例
函数y=kx(x>0)的图象交于A,B两点,已知A点坐标为(2,4).
(1)求一次函数和反比例函数的解析式;
(2)连接AO,BO,求△AOB的面积?
)页4共(页3第卷试学数级年九市埠蚌
六、(本题满分12分)
21?如图,某海域灯塔D的正东方向有一岛屿C?一艘快艇以每小时20nmile的速度向正东方
向航行,到达A处时测得灯塔D在东北方向上,继续航行0?3h,到达B处时测得灯塔D在
北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离
是多少?(结果精确到1nmile?参考数据:槡2≈1?41,槡3≈1?73,槡6≈2?45)
第21题图
七、(本题满分12分)
22?如图,在△ABC中,AB=AC=13,BC=10,AG⊥BC于 G点,D是 BC上的点,DE⊥AB于 E
第22题图
点,DF∥AB,交AC于点F?
(1)求证:△DBE∽△ABG;
(2)当△DEF的面积最大时,求BD的长?
八、(本题满分14分)
23?如图(1),矩形 ABCD中,AB=a,BC=b,点 M,N分别在边 AB,CD上,点 E,F分别在边
BC,AD上,MN,EF交于点P,记k=MN∶EF?
(1)如图(2)若a∶b的值为1,当MN⊥EF时,求k的值?
(2)若k的值为3,当点N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a∶b的值?
图(1) 图(2)
第23题图
)页4共(页4第卷试学数级年九市埠蚌
蚌埠市2019—2020学年度第一学期期末教学质量监测
九年级数学参考答案和评分标准(沪科版)
一、选择题:(本大题共10小题,每小题4分,共40分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 A B D B B A C D C A
二、填空题:(本大题共4个小题,每小题5分,共20分)
11?12 12?x<-2或0<x<4 13?5 14?125或
48
11
三、本题共两小题,每小题8分,共16分
15?解:原式=2×槡32 槡-1-|1-3| 4分…………………………………………………………
=0. 8分………………………………………………………………………………
16?解:过B点作BD⊥AC于点D,由三角形面积公式可求得BD 槡=43, 3分…………………
由勾股定理得AD=4, 6分…………………………………………………………………
所以cosA=12. 8分………………………………………………………………………
四、本题共两小题,每小题8分共16分
17?解:(1)以点O为位似中心,将△ABC缩小为原来的
1
2,得到△A1B1C1,请在y轴右侧画出△A1B1C1;
4分…………………………………………
(2)槡1010? 8分…………………………………
18?解:连接AC?
∵∠B=60°,AB=BC,
∴△ABC是等边三角形, 2分…………………
设AB=BC=AC=a,则BH=a-7,BG=a-3,
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,
∵∠AGH=∠ACG=60°,∴∠BGH=∠CAG,
∵∠B=∠ACG,∴△BGH∽△CAG, 5分……………
∴BGAC=
BH
CG,∴
a-3
a =
a-7
3 ,
∴a2-10a+9=0,∴a=9或a=1(舍),
∴AB=9. 8分…………………………………………
)页4共(页1第 准标分评和案答考参卷试学数级年九市埠蚌
19?(本题满分10分)
解:(1)由题意得,抛物线的顶点坐标为(3,9),且经过(5,10).
设y2与x之间的函数关系式为:y2=a(x-3)
2+9, 2分……………………………
将(5,10)代入y2=a(x-3)
2+9得a(5-3)2+9=10,
解得:a=14,
∴y2=
1
4(x-3)
2+9=14x
2-32x+
45
4. 5分…………………………………………
(2)由题意得,
w=y1-y2=2x+6-(
1
4x
2-32x+
45
4)
=-14x
2+72x-
21
4=-
1
4(x-7)
2+7。 7分………………………………………
∴当x=7时,w取最大值7?
∴7月份利润最大,最大利润为7元。 10分…………………………………………
20?(本题满分10分)
解:(1)将A(2,4)代入y=-x+m与y=kx(x>0)得4=-2+m,4=
k
2, 2分…………
∴m=6,k=8,
∴一次函数的解析式为y=-x+6,反比例函数的解析式为y=8x; 4分…………
(2)解方程组
y=-x+6,
y=8x
{ . 得 x=2,y=4{ ,或 x=4,y=2{ . ∴B(4,2), 6分………………………
设直线y=-x+6与x轴,y轴交于C,D点,易得D(0,6),即OD=6, 8分………
∴S△AOB=S△DOB-S△AOD=6? 10分……………………………………………………
21?(本题满分12分)
解:过点D作DE⊥AB于点E,过点C作CF⊥AB于
点F,如图所示?
则DE∥CF,∠DEA=∠CFA=90°?
即CDEF为矩形,∴CF=DE?
依题意DC∥EF,AD∥BC,∴四边形CDEF为平行四边形? 4分………………………
根据题意,得:∠DAB=45°,∠DBE=60°,∠CBF=45°?
)页4共(页2第 准标分评和案答考参卷试学数级年九市埠蚌
设DE=x(nmile),则AE=x(nmile)?
在Rt△DEB中,∵tan∠DBE=DEBE 槡=3,∴BE=
槡3
3x(nmile)? 8分……………………
∵AB=AE-BE=20×0?3=6(nmile),
∴x-槡33x=6,解得:x 槡=9+33,
∴CF=DE=( 槡9+33)nmile?
在Rt△CBF中,sin∠CBF=CFBC=
槡2
2,∴BC 槡 槡=92+36≈20(nmile)?
答:此时快艇与岛屿C的距离是20nmile? 12分…………………………………………
22?(本题满分12分)
解:(1)证明:∵DE⊥AB,AG⊥BC,∴∠BED=∠AGB=90°,
∵∠B=∠B,∴△DBE∽△ABG? 4分………………………………………………
(2)解:BC=10,BG=5,AG=12,BD=x,CD=10-x,ED=1213x,
∵DF∥AB,∴DFAB=
CD
CB,
∴DF=1?3(10-x),
∴ΔDEF的面积S=12×
12
13x×1?3(10-x)=0?6x(10-x). 8分…………………
=-0?6(x-5)2+15,
∵当△DEF的面积最大时,x=5,即BD的长为5 12分……………………………
23?(本题满分14分)
解:(1)如图1,作EH⊥BC于H,MQ⊥CD于Q,设EF交MN于点O?
∵四边形ABCD是正方形,∴FH=AB,MQ=BC,
∴AB=CB,∴EH=MQ,
∵EF⊥MN,∴∠EON=90°,
∵∠ECN=90°,∴∠MNQ+∠CEO=180°,∠FEH+∠CEO=180°
∴∠FEH=∠MNQ,∵∠EHF=∠MQN=90°,
∴ΔFHE≌ΔMQN, 4分…………………………………………………………………
∴MN=EF,∴k=MN∶EF=1? 6分…………………………………………………
(2)连接FN,ME?
)页4共(页3第 准标分评和案答考参卷试学数级年九市埠蚌
∵k=3,MP=EF=3PE,∴MNPM=
3EF
3PE=
EF
PE=3,
∴PNPM=
PF
PE=2,又∠FPN=∠EPM,
∴ΔPNF∽ΔPEM,∴NFME=
PN
PM=2,ME∥NF, 9分……………………………………
设PE=2m,则PF=4m,MP=6m,NP=12m,
①如图2,当点N与点D重合时,点M恰好与B重合?作FH⊥BD于H?
∵∠MPE=∠FPH=60°,∴PH=2m,FH 槡=23m,DH=10m,
∴ab=
AB
AD=
FH
HD=
槡3
5? 11分…………………………………………………………
②如图3,当点N与C重合,作EH⊥MN于H?则PH=m,HE 槡=3m,
∴HC=PH+PC=13m,∴tan∠HCE=MBBC=
HE
HC=
槡3
13,
∵ME∥FC,∴∠MEB=∠FCB=∠CFD,
∵∠B=∠D,∴ΔMEB∽ΔCFD,
∴CDMB=
FC
ME=2,∴
a
b=
CD
BD=
2MB
BC=
槡23
13,
综上所述,a∶b的值为槡35或
槡23
13? 14分………………………………………………
图1 图2 图3
(其它解法请根据以上评分标准酌情赋分)
)页4共(页4第 准标分评和案答考参卷试学数级年九市埠蚌
同课章节目录
