北京课改版九年级数学上册第18章 相似形 综合测试卷(含答案)
文档属性
| 名称 | 北京课改版九年级数学上册第18章 相似形 综合测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 19:19:25 | ||
图片预览




文档简介
北京版九年级数学上册
第18章 相似形
综合测试卷
(时间90分钟,满分120分)
一、选择题(共10小题,3*10=30)
1.下面关于直角三角形相似叙述错误的是( )
A.有一锐角对应相等的两直角三角形相似
B.两直角边对应成比例的两直角三角形相似
C.有一条直角边相等的两个直角三角形相似
D.两个等腰直角三角形相似
2.下列各组长度的线段,成比例线段的是( )
A.2 cm,4 cm,4 cm,8 cm
B.2 cm,4 cm,6 cm,8 cm
C.1 cm,2 cm,3 cm,4 cm
D.2.1 cm,3.1 cm,4.3 cm,5.2 cm
3.顺次连接正方形各边中点所得的四边形一定是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
4.如图,若AB∥CD∥EF,则下列结论中,与相等的是( )
A. B. C. D.
5.在平面直角坐标系中,已知点A(-4,2),B(-6,-4),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-2,1) B.(-8,4)
C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
6.如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE∶S△CDE=1∶4,则S△BDE∶S△ACD等于( )
A.1∶16 B.1∶18
C.1∶20 D.1∶24
,
7.如图,在?ABCD中,AC与BD相交于点O,点E是边BC的中点,AB=4,则OE的长是( )
A.2 B. C.1 D.
8.在平行四边形ABCD中,点E在AD上,且AE∶ED=3∶1,CE的延长线与BA的延长线交于点F,则S△AEF∶S四边形ABCE为( )
A.3∶4 B.4∶3
C.7∶9 D.9∶7
9.为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如图,如果大视力表中“E”的高度是3.5 cm,那么小视力表中相应“E”的高度是( )
A.2.1 cm B.2.5 cm
C.2.3 cm D.3 cm
10.如图,在Rt△ABC中,∠C=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t s,若四边形QPCP′为菱形,则t的值为( )
A. B.2
C.2 D.3
二.填空题(共8小题,3*8=24)
11.若===≠0,则=________.
12.有一块三角形的草地,它的一条边长为25 m.在图纸上,这条边的长为5 cm,其他两条边的长都为4 cm,则其他两边的实际长度都是________ m.
13.如图,乐器上的一根弦AB=80 cm,两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,则支撑点C到端点A的距离约为________(≈2.236,结果精确到0.01).
14.如图在两个直角三角形中,∠ACB=∠ADC=90°,AC=,AD=2.当AB=________时,△ABC∽△ACD.
15.如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F,若BF= cm,则EF=________.
16.若两个相似多边形的面积之比为1∶4,周长之差为6,则这两个相似多边形的周长分别是________.
17.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5).若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为_______________________.
18.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=6,BC=8,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是________.
三.解答题(共7小题, 66分)
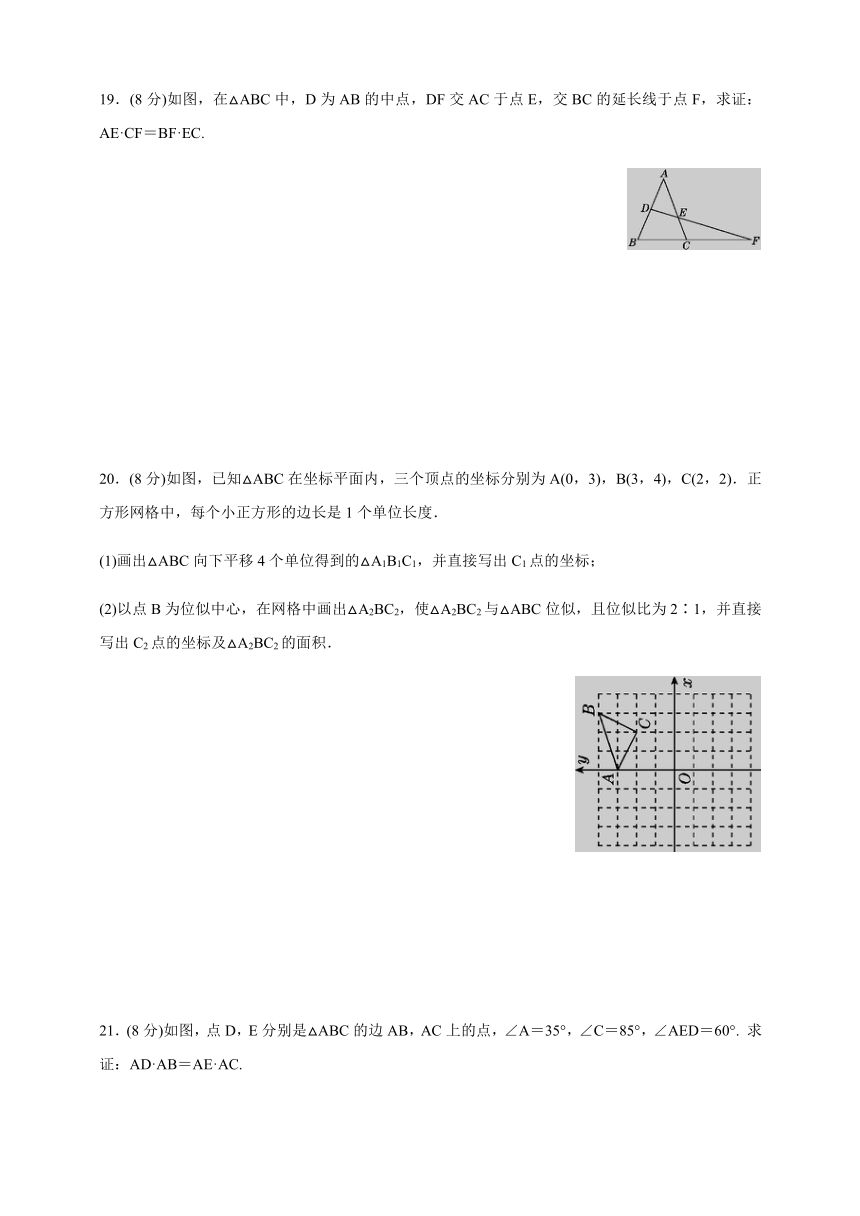
19.(8分)如图,在△ABC中,D为AB的中点,DF交AC于点E,交BC的延长线于点F,求证:AE·CF=BF·EC.
20.(8分)如图,已知△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2∶1,并直接写出C2点的坐标及△A2BC2的面积.
21.(8分)如图,点D,E分别是△ABC的边AB,AC上的点,∠A=35°,∠C=85°,∠AED=60°. 求证:AD·AB=AE·AC.
22.(10分) 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,E为AC的中点,ED的延长线交AB的延长线于点F.求证:=.
23.(10分) 如图,已知点D为等腰直角三角形ABC的斜边AB上一点,连接CD,DE⊥CD,DE=CD,连接CE,AE.求证:AE∥BC.
24.(10分) 亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算楼高,但恰逢阴天,于是两人商定改用下面的方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距离CD=1.25 m,颖颖与楼之间的距离DN=30 m(C,D,N在一条直线上),颖颖的身高DB=1.6 m,亮亮蹲地观测时眼睛到地面的距离AC=0.8 m,你能根据以上测量数据帮助他们求出住宅楼的高吗?
25.(12分)如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE·BC=BD·AC.
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.
参考答案
1-5 CADDD
6-10 CADAB
11.4
12.20
13.49.44 cm
14.3
15.3 cm
16.6,12
17. (3,4)或(0,4)
18.4或
19.证明:过点C作CM∥AB交DF于点M,
∵CM∥AB,△CMF∽△BDF.
∴=.
又∵CM∥AD,∴=.∵D为AB的中点,
∴=.∴=,即AE·CF=BF·EC.
20.解:(1)如图所示,△A1B1C1即为所求,C1(2,-2);
(2)如图所示,△A2BC2即为所求,C2(1,0),S△A2B C2=10.
21.证明:∵∠A=35°,∠C=85°,
∴∠B=180°-∠A-∠C=180°-35°-85°=60°.
∵∠AED=60°,∴∠AED=∠B.
又∵∠A=∠A,∴△ADE∽△ACB.
∴=,即AD·AB=AE·AC.
22.证明:∵∠BAC=90°,AD⊥BC于点D,
∴∠BAC=∠ADB=90°.
又∵∠CBA=∠ABD(公共角),
∴△ABC∽△DBA.∴=,∠BAD=∠C.
∵AD⊥BC于点D,E为AC的中点,∴DE=EC=EA.
∴∠BDF=∠CDE=∠C.∴∠BDF=∠BAD.
又∵∠F=∠F,
∴△DBF∽△ADF.∴=.∴=.
23.证明:过点C作CO⊥AB于点O,∵DE=CD,DE⊥CD,
∴∠ECD=∠CED=45°.∵∠ACB=90°,AC=BC,∴∠CAB=∠B=45°.∴∠CAB=∠CED.又∵∠AOC=∠EDC=90°,
∴△ACO∽△ECD.
∴=.
又∵∠ACE+∠ECO=∠OCD+∠ECO=45°,∴∠ACE=∠OCD.
∴△ACE∽△OCD.∴∠CAE=∠COD=90°.又∵∠ACB=90°,∴∠CAE+∠ACB=180°.∴AE∥BC.
24. 解:过点A作CN的平行线交BD于点E,交MN于点F,由已知可得FN=ED=AC=0.8 m,AE=CD=1.25 m,EF=DN=30 m,∠AEB=∠AFM=90°,又∵∠BAE=∠MAF,∴△ABE∽△AMF,∴=,即=,解得MF=20 m,∴MN=MF+FN=20+0.8=20.8(m).故住宅楼的高为20.8 m
24.(1)证明:∵ED∥BC,∴=.
∵∠A是公共角,∴△ADE∽△ABC.∴=.
∵BE平分∠ABC,∴∠DBE=∠EBC.
∵ED∥BC,∴∠DEB=∠EBC.
∴∠DBE=∠DEB.∴DE=BD.
∴=,
即AE·BC=BD·AC.
(2)解:设h△ADE表示△ADE中DE边上的高,
h△BDE表示△BDE中DE边上的高,
h△ABC表示△ABC中BC边上的高,
∵S△ADE=3,S△BDE=2,∴==.
∴=.
∵△ADE∽△ABC,∴==.
∵DE=6,∴BC=10.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
