人教版数学七年级下册:7.1.2 平面直角坐标系 课件(共21张PPT)
文档属性
| 名称 | 人教版数学七年级下册:7.1.2 平面直角坐标系 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 20:02:25 | ||
图片预览




文档简介
(共21张PPT)
平面直角坐标系
·
0
1
2
3
4
-3
-2
-1
原点
.
.
利用数轴可以确定直线上点的位置,
平面内点的位置如何确定呢?
B
A
温故知新
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
原点
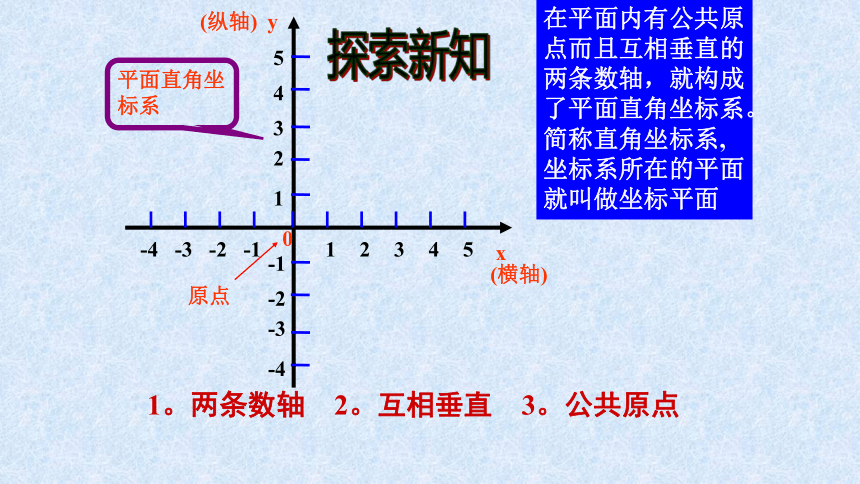
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系。简称直角坐标系,坐标系所在的平面就叫做坐标平面
探索新知
平面直角坐标系
1。两条数轴 2。互相垂直 3。公共原点
(横轴)
(纵轴)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
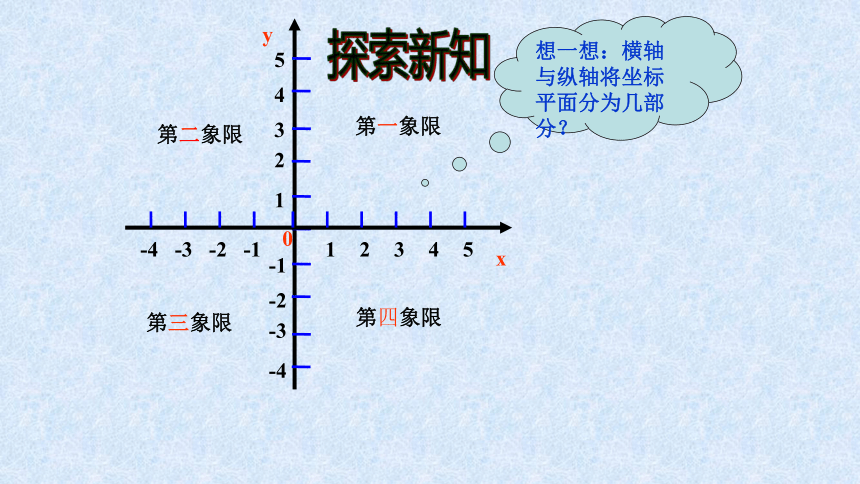
第一象限
第四象限
第三象限
第二象限
想一想:横轴与纵轴将坐标平面分为几部分?
探索新知
(2,3)
( - 4 , 1 )
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
(3,2)
·
C
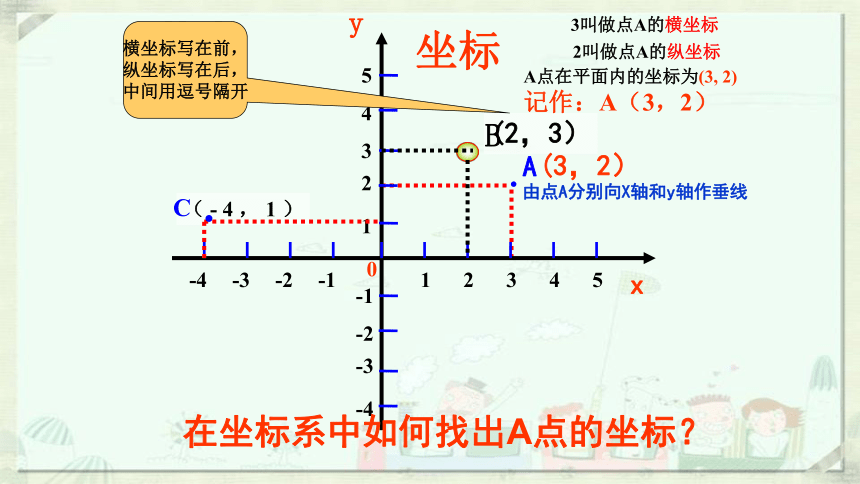
由点A分别向X轴和y轴作垂线
B
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3, 2)
记作:A(3,2)
横坐标写在前,
纵坐标写在后,
中间用逗号隔开
坐标
在坐标系中如何找出A点的坐标?
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
A
( 4,3 )
2
与你共探究
在平面直角坐标系中
如何有坐标描点?
( 4,3 )
A
让我们一块来做游戏
两只小蜜蜂飞在花丛中,飞到东来飞到西。
A(﹣4,0)的家出发沿着 B(-2,-2)
C(-2,0) D(3,-2) E(5,0) F(2,0)
G(2,5) H(-1,3) I(2,3) F(2,0) A(﹣4,0)的路线飞了一圈
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
·
·
·
·
A
B (-2,-2)
(3,-2)
·
·
·
·
D
E
F
·
H
G
(﹣4,0)
(5,0)
(2,0)
(2,5)
(-1,3)
(2,3)
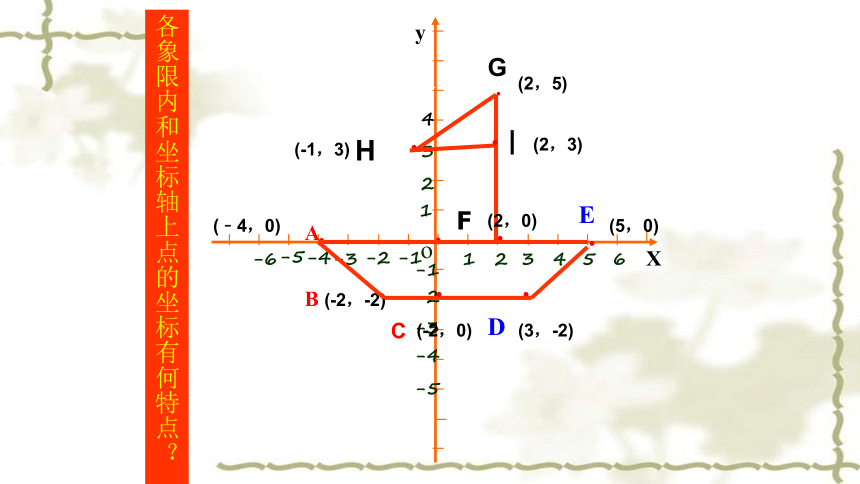
把各点连接起来会得到什么图形?
·
(-2,0)
C
I
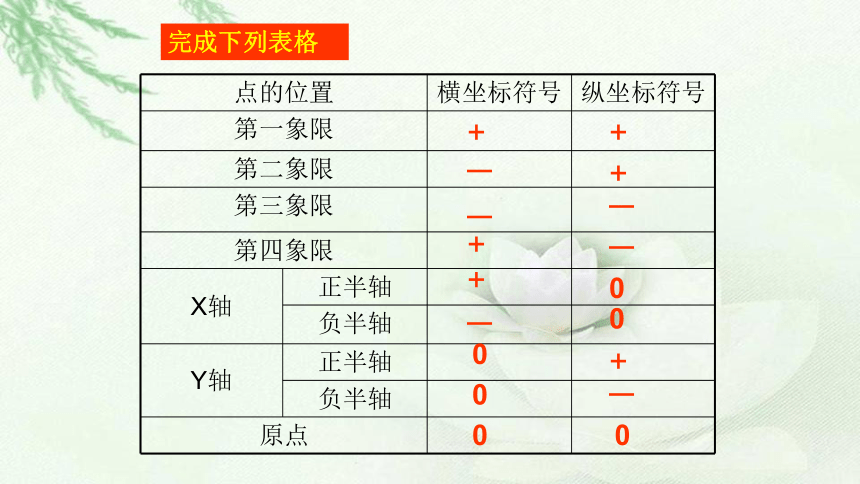
各象限内和坐标轴上点的坐标有何特点?
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
X轴 正半轴
负半轴
Y轴 正半轴
负半轴
原点
完成下列表格
+
+
+
+
—
—
—
—
—
—
0
0
0
0
0
0
+
+
大胆择题 勇于闯关
1
4
3
2
过关斩将,及时反馈
5
6
风险题
1.横坐标为负,纵坐标为正的点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
希望这道题能给你带来好运!
2.如果a-b<0,且ab<0,那么点(a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
希望这道题能给你带来好运!
下列说法正确的有----------------
(1)直角坐标系中,点(3,0)在横轴上,点(0,-3)在纵轴上
(2)直角坐标系中,原点既在X轴上又在Y轴上
(3)(2,-5)与(-5,2)表示两个不同的点
(4)仅有两条互相垂直的直线就可以组成平面直角坐标系
(1) (2) (3)
希望这道题能给你带来好运!
希望这道题能给你带来好运!
1.点A(3,4)到x轴的距离是( ),
到y轴的距离是( );
2.点B(0,9)到x轴的距离是( ),
到y轴的距离是( );
3.C (9,0)到x轴的距离是( )
,到y轴的距离是( );
若点P(a,b)是第四象限的点,且︱a ︱ =2, ︱ b ︱ =3,则p的坐标是( )
A. (2,-3) B.(-2,3)
C.(-3,2) D.(3,-2)
A
希望这道题能给你带来好运!
已知X轴上的P到y轴的距离为3,则点p的坐标为( )
希望这道题能给你带来好运!
若点(a+5,a-3),
则a的值为( )
该点的坐标为( )
希望这道题能给你带来好运!
在y轴上
在x轴上
在同一坐标系中,如果(3a+1,
b-2)与(-5,1)所示的位置
相同,则a=( )b=( )
希望这道题能给你带来好运!
已知(a-2)2 + ︱ b+3 ︱=0,
则P(-a,-b)的坐标为( )
希望这道题能给你带来好运!
拓 展 应 用 变 练 演 编
老师相信你一定能利用平面直角
坐标系内的点设计出更好的图案
回顾梳理,互动返悟
我对同学说:
1、我学到了什么?
2、我向你学习什么?
3、我提醒你注意什么?
我对老师说:
我有哪些感触或困惑?
平面直角坐标系
·
0
1
2
3
4
-3
-2
-1
原点
.
.
利用数轴可以确定直线上点的位置,
平面内点的位置如何确定呢?
B
A
温故知新
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
原点
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系。简称直角坐标系,坐标系所在的平面就叫做坐标平面
探索新知
平面直角坐标系
1。两条数轴 2。互相垂直 3。公共原点
(横轴)
(纵轴)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
第一象限
第四象限
第三象限
第二象限
想一想:横轴与纵轴将坐标平面分为几部分?
探索新知
(2,3)
( - 4 , 1 )
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
(3,2)
·
C
由点A分别向X轴和y轴作垂线
B
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3, 2)
记作:A(3,2)
横坐标写在前,
纵坐标写在后,
中间用逗号隔开
坐标
在坐标系中如何找出A点的坐标?
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
A
( 4,3 )
2
与你共探究
在平面直角坐标系中
如何有坐标描点?
( 4,3 )
A
让我们一块来做游戏
两只小蜜蜂飞在花丛中,飞到东来飞到西。
A(﹣4,0)的家出发沿着 B(-2,-2)
C(-2,0) D(3,-2) E(5,0) F(2,0)
G(2,5) H(-1,3) I(2,3) F(2,0) A(﹣4,0)的路线飞了一圈
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
·
·
·
·
A
B (-2,-2)
(3,-2)
·
·
·
·
D
E
F
·
H
G
(﹣4,0)
(5,0)
(2,0)
(2,5)
(-1,3)
(2,3)
把各点连接起来会得到什么图形?
·
(-2,0)
C
I
各象限内和坐标轴上点的坐标有何特点?
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
X轴 正半轴
负半轴
Y轴 正半轴
负半轴
原点
完成下列表格
+
+
+
+
—
—
—
—
—
—
0
0
0
0
0
0
+
+
大胆择题 勇于闯关
1
4
3
2
过关斩将,及时反馈
5
6
风险题
1.横坐标为负,纵坐标为正的点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
希望这道题能给你带来好运!
2.如果a-b<0,且ab<0,那么点(a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
希望这道题能给你带来好运!
下列说法正确的有----------------
(1)直角坐标系中,点(3,0)在横轴上,点(0,-3)在纵轴上
(2)直角坐标系中,原点既在X轴上又在Y轴上
(3)(2,-5)与(-5,2)表示两个不同的点
(4)仅有两条互相垂直的直线就可以组成平面直角坐标系
(1) (2) (3)
希望这道题能给你带来好运!
希望这道题能给你带来好运!
1.点A(3,4)到x轴的距离是( ),
到y轴的距离是( );
2.点B(0,9)到x轴的距离是( ),
到y轴的距离是( );
3.C (9,0)到x轴的距离是( )
,到y轴的距离是( );
若点P(a,b)是第四象限的点,且︱a ︱ =2, ︱ b ︱ =3,则p的坐标是( )
A. (2,-3) B.(-2,3)
C.(-3,2) D.(3,-2)
A
希望这道题能给你带来好运!
已知X轴上的P到y轴的距离为3,则点p的坐标为( )
希望这道题能给你带来好运!
若点(a+5,a-3),
则a的值为( )
该点的坐标为( )
希望这道题能给你带来好运!
在y轴上
在x轴上
在同一坐标系中,如果(3a+1,
b-2)与(-5,1)所示的位置
相同,则a=( )b=( )
希望这道题能给你带来好运!
已知(a-2)2 + ︱ b+3 ︱=0,
则P(-a,-b)的坐标为( )
希望这道题能给你带来好运!
拓 展 应 用 变 练 演 编
老师相信你一定能利用平面直角
坐标系内的点设计出更好的图案
回顾梳理,互动返悟
我对同学说:
1、我学到了什么?
2、我向你学习什么?
3、我提醒你注意什么?
我对老师说:
我有哪些感触或困惑?
