北师大版数学九年级下册课件2.5.1 二次函数与一元二次方程之间的关系(23张PPT)
文档属性
| 名称 | 北师大版数学九年级下册课件2.5.1 二次函数与一元二次方程之间的关系(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-27 19:46:16 | ||
图片预览







文档简介
课件23张PPT。第二章
二次函数2.5.1 二次函数与一元二次方程之间的关系九年级数学北师版·下册教学目标1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,理解何时方程有两个不等的实数根、两个相等的实数根和没有实数根.
3.理解一元二次方程的根就是二次函数与x轴交点的横坐标.新课导入情境引入1.一元二次方程ax2+bx+c=0 的求根公式是什么?当b2-4ac≥0时,当b2-4ac<0时,方程无实数根.新课导入2 . 求出下列一元二次方程的根:
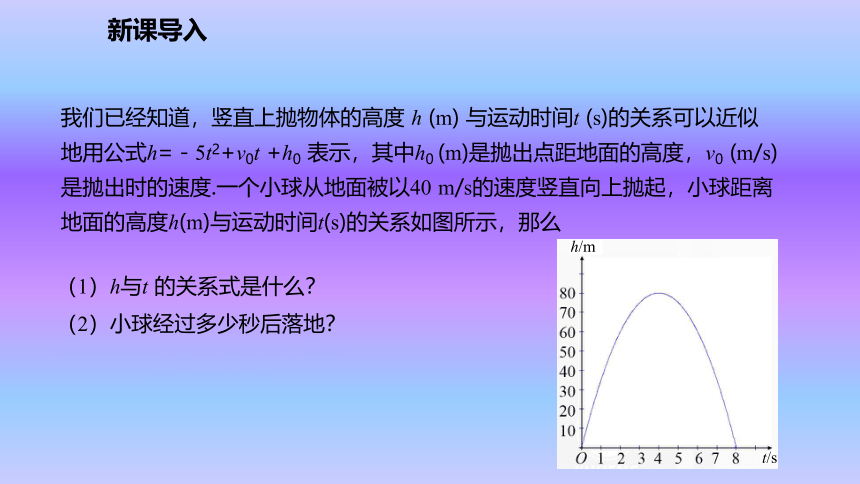
(1)x2+2x=0 (2)x2-2x+1=0 (3)x2-2x+2=0 .解:(1)x1=0, x2=-2.(2)x1=x2=1.(3)没有实数根.新课导入我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t (s)的关系可以近似地用公式h=-5t2+v0t +h0 表示,其中h0 (m)是抛出点距地面的高度,v0 (m/s)是抛出时的速度.一个小球从地面被以40 m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示,那么(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?h/mt/s新知探究解:(1)由图象知函数过点(0,0)与点(8,0)
代入关系式h=-5t2+v0t+h0得h0=0, 由已知可知v0=40,
得h=-5t2+40t.(2)由图象可知小球经过8秒后落地.可以令h=0,
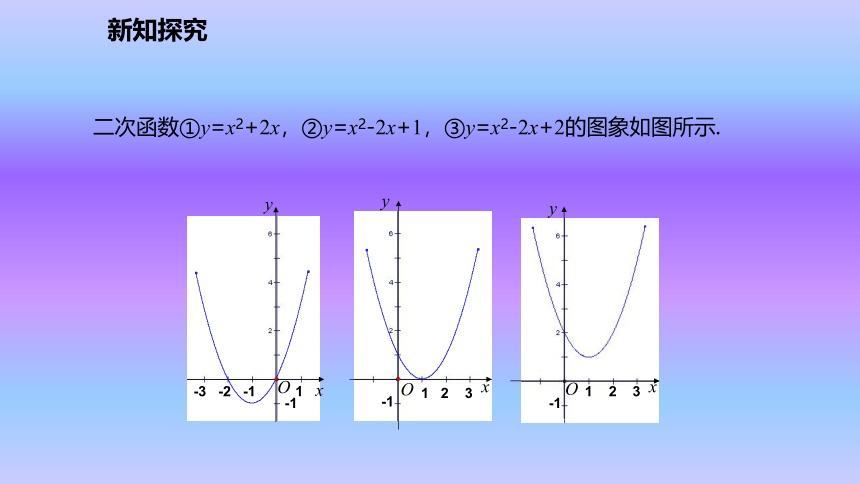
得t=0s(舍去)或t=8s.新知探究二次函数①y=x2+2x,②y=x2-2x+1,③y=x2-2x+2的图象如图所示. 新知探究(1)每个图象与x轴有几个交点?
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根?
用判别式验证一下,一元二次方程x2-2x+2=0有实数根吗?
(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?新知探究(2)①x1=0, x2=-2,两个不相等实数根.②x1=x2=1,两个相等实数根.③没有实数根.解:(1)每个图象与x轴的交点个数分别是2个,1个,0个.(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐
标就是一元二次方程ax2+bx+c=0的根.新知探究例题:已知关于x的一元二次方程x2-(m+1)x+ (m2+1)=0有实数根.
(1)求m的值.(2)先作y=x2-(m+1)x+ (m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2-4n的最大值和最小值.新知探究思路点拨:
(1)由题意Δ≥0,列出不等式,解不等式即可.
(2)画出翻折、平移后的图象,根据顶点坐标即可写出函数的解析式.
(3)首先确定n的取值范围,利用二次函数的性质即可解决问题.新知探究新知探究(2)由(1)可知y=x2-2x+1=(x-1)2,
图象如图所示:
平移后的解析式为y=-(x+2)2+2=-x2-4x-2.新知探究(3)由
消去y得到x2+6x+n+2=0,
由题意Δ≥0,
∴36-4n-8≥0,∴n≤7,
∵n≥m,m=1,
∴1≤n≤7,令y′=n2-4n=(n-2)2-4,
∴当n=2时,y′的值最小,最小值为-4,
当n=7时,y′的值最大,最大值为21,
∴n2-4n的最大值为21,最小值为-4.新知探究点拨 :1.b2-4ac>0?抛物线与x轴有2个交点?方程有两个不相等的实数根.
2.b2-4ac=0?抛物线与x轴有1个交点?方程有两个相等的实数根.
3.b2-4ac<0?抛物线与x轴没有交点?方程没有实数根.二次函数y=ax2+bx+c与方程ax2+bx+c=0之间的关系:新知探究1.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴的交点情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定C【跟踪训练】2.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的解是 .x1=0,x2=5新知探究1116?(-2,0)课堂小结1.二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是
一元二次方程ax2+bx+c=0的根.2.b2-4ac>0?抛物线与x轴有2个交点?方程有两个不相等的实数根.
3.b2-4ac=0?抛物线与x轴有1个交点?方程有两个相等的实数根.
4.b2-4ac<0?抛物线与x轴没有交点?方程没有实数根.二次函数y=ax2+bx+c与方程ax2+bx+c=0之间的关系:课堂小测1. 如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A, B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2)
C.(3,3) D.(4,3)D 课堂小测2.已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式.
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.课堂小测故所求解析式为y=-x2+2x+3 .解得x1=-1, x2=3,∴由图象可知,函数值y为正数时,自变量x的取值范围
是-1<x<3.(2)令y=0,得-x2+2x+3=0,∴抛物线与x轴的另一个交点坐标为(3 , 0) ,课堂小测3.已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)证明:4c=3b2.
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.∴二次函数的最小值为-4.解 :(1)证明:依题意知m,-3m是一元二次方程x2+bx-c=0的两个根.
根据一元二次方程根与系数的关系,
得m+(-3m)=-b , m·(-3m)=-c ,
b=2m , c=3m2 ,
∴4c=12m2=3b2 .?课堂小测
2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,理解何时方程有两个不等的实数根、两个相等的实数根和没有实数根.
3.理解一元二次方程的根就是二次函数与x轴交点的横坐标.新课导入情境引入1.一元二次方程ax2+bx+c=0 的求根公式是什么?当b2-4ac≥0时,当b2-4ac<0时,方程无实数根.新课导入2 . 求出下列一元二次方程的根:
(1)x2+2x=0 (2)x2-2x+1=0 (3)x2-2x+2=0 .解:(1)x1=0, x2=-2.(2)x1=x2=1.(3)没有实数根.新课导入我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t (s)的关系可以近似地用公式h=-5t2+v0t +h0 表示,其中h0 (m)是抛出点距地面的高度,v0 (m/s)是抛出时的速度.一个小球从地面被以40 m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示,那么(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?h/mt/s新知探究解:(1)由图象知函数过点(0,0)与点(8,0)
代入关系式h=-5t2+v0t+h0得h0=0, 由已知可知v0=40,
得h=-5t2+40t.(2)由图象可知小球经过8秒后落地.可以令h=0,
得t=0s(舍去)或t=8s.新知探究二次函数①y=x2+2x,②y=x2-2x+1,③y=x2-2x+2的图象如图所示. 新知探究(1)每个图象与x轴有几个交点?
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个实数根?
用判别式验证一下,一元二次方程x2-2x+2=0有实数根吗?
(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?新知探究(2)①x1=0, x2=-2,两个不相等实数根.②x1=x2=1,两个相等实数根.③没有实数根.解:(1)每个图象与x轴的交点个数分别是2个,1个,0个.(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐
标就是一元二次方程ax2+bx+c=0的根.新知探究例题:已知关于x的一元二次方程x2-(m+1)x+ (m2+1)=0有实数根.
(1)求m的值.(2)先作y=x2-(m+1)x+ (m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2-4n的最大值和最小值.新知探究思路点拨:
(1)由题意Δ≥0,列出不等式,解不等式即可.
(2)画出翻折、平移后的图象,根据顶点坐标即可写出函数的解析式.
(3)首先确定n的取值范围,利用二次函数的性质即可解决问题.新知探究新知探究(2)由(1)可知y=x2-2x+1=(x-1)2,
图象如图所示:
平移后的解析式为y=-(x+2)2+2=-x2-4x-2.新知探究(3)由
消去y得到x2+6x+n+2=0,
由题意Δ≥0,
∴36-4n-8≥0,∴n≤7,
∵n≥m,m=1,
∴1≤n≤7,令y′=n2-4n=(n-2)2-4,
∴当n=2时,y′的值最小,最小值为-4,
当n=7时,y′的值最大,最大值为21,
∴n2-4n的最大值为21,最小值为-4.新知探究点拨 :1.b2-4ac>0?抛物线与x轴有2个交点?方程有两个不相等的实数根.
2.b2-4ac=0?抛物线与x轴有1个交点?方程有两个相等的实数根.
3.b2-4ac<0?抛物线与x轴没有交点?方程没有实数根.二次函数y=ax2+bx+c与方程ax2+bx+c=0之间的关系:新知探究1.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴的交点情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定C【跟踪训练】2.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的解是 .x1=0,x2=5新知探究1116?(-2,0)课堂小结1.二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是
一元二次方程ax2+bx+c=0的根.2.b2-4ac>0?抛物线与x轴有2个交点?方程有两个不相等的实数根.
3.b2-4ac=0?抛物线与x轴有1个交点?方程有两个相等的实数根.
4.b2-4ac<0?抛物线与x轴没有交点?方程没有实数根.二次函数y=ax2+bx+c与方程ax2+bx+c=0之间的关系:课堂小测1. 如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A, B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2)
C.(3,3) D.(4,3)D 课堂小测2.已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式.
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.课堂小测故所求解析式为y=-x2+2x+3 .解得x1=-1, x2=3,∴由图象可知,函数值y为正数时,自变量x的取值范围
是-1<x<3.(2)令y=0,得-x2+2x+3=0,∴抛物线与x轴的另一个交点坐标为(3 , 0) ,课堂小测3.已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)证明:4c=3b2.
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.∴二次函数的最小值为-4.解 :(1)证明:依题意知m,-3m是一元二次方程x2+bx-c=0的两个根.
根据一元二次方程根与系数的关系,
得m+(-3m)=-b , m·(-3m)=-c ,
b=2m , c=3m2 ,
∴4c=12m2=3b2 .?课堂小测
