北师大版九年级数学下册课件 3.3 垂径定理(23张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件 3.3 垂径定理(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-13 20:52:40 | ||
图片预览







文档简介
课件23张PPT。第三章
圆3.3 垂径定理九年级数学北师版·下册教学目标1.通过手脑结合,充分掌握圆的轴对称性.
2.运用探索、推理,充分把握圆中的垂径定理及其逆定理.
3.拓展思维,与实践相结合,运用垂径定理及其逆定理进行
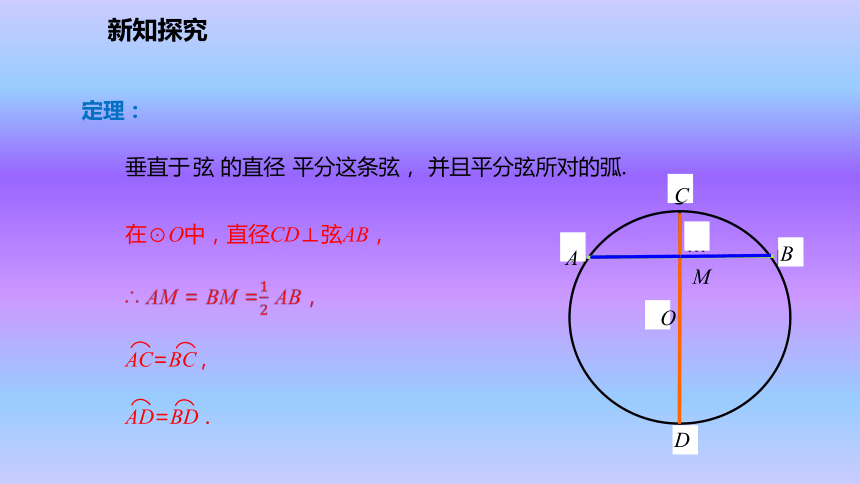
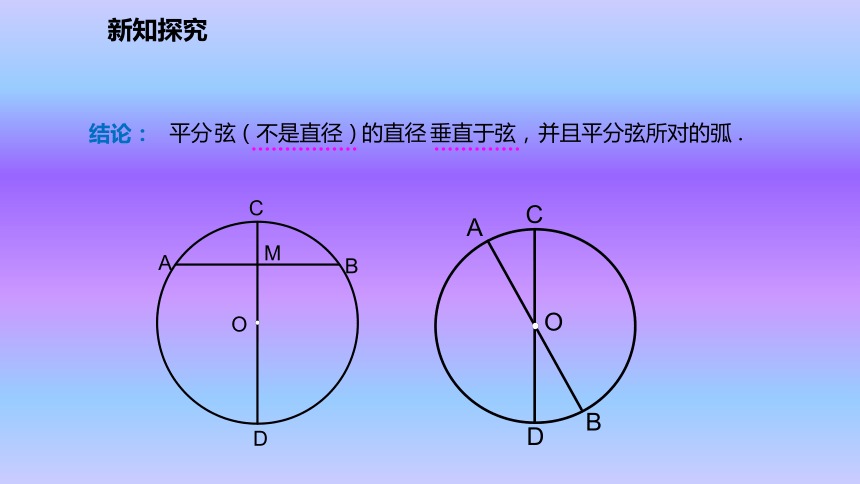
有关的计算和证明.新课导入情境引入点在圆外,这个点到圆心的距离大于半径 点在圆上,点在圆内,这个点到圆心的距离等于半径 这个点到圆心的距离小于半径 点与圆的位置关系新课导入2.它的对称轴是什么?是圆的对称轴是任意一条经过圆心的直线3.你能找到多少条对称轴?它有无数条对称轴.1.圆是轴对称图形吗?新知探究③AM=BM,AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.小明发现图中有:①CD是直径②CD⊥AB【问题】新知探究连接OA,OB,则OA=OB.●OCD └在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,理 由:M新知探究垂直于平分这条弦,并且平分弦所对的弧. 弦的直径在⊙O中,直径CD⊥弦AB,?定理:ABCDOM新知探究┗在⊙O中,直径CD平分弦AB,∴ CD⊥AB,平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.定理:新知探究弦(不是直径)并且平分弦所对的弧 . 平分的直径垂直于弦, 结论:新知探究1.在⊙O中,OC垂直于弦AB,AB = 8,
OA = 5,则AC= ,OC = .┏58432.在⊙O中,OC平分弦AB,AB = 16,
OA = 10,则∠OCA = °,
OC = .1610906【巩固练习】新知探究例1 . 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB .└新知探究解:连接OA,在⊙O中,直径CD⊥AB,∴ AB =2AM,△OMA是直角三角形.∵ CD = 20,∴ AO = CO = 10.∴ OM = OC – CM = 10 – 4 = 6.在Rt△OMA中,AO = 10,OM = 6,根据勾股定理,得:AO2=OM2+AM2,∴ AB = 2AM = 2 × 8 = 16.└?新知探究例2 . 如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.你认为AC与BD的大小有什么关系?为什么?解 : 作OG⊥AB,
∵AG=BG,CG=DG,
∴AC=BD.G新知探究└解 : 连接OC.设弯路的半径为Rm,则OF=(R-90)m.根据勾股定理,得OC2=CF2+OF2,即解这个方程,得R=545,∴这段弯路的半径为545m .新知探究1.判断:
(1)垂直于弦的直线平分这条弦,并且平分弦所对的两
条弧. ( )
(2)平分弦所对的一条弧的直径一定平分这条弦所对
的另一条弧. ( )
(3)经过弦的中点的直径一定垂直于弦. ( )
(4)弦的垂直平分线一定平分这条弦所对的弧( )对错错对【跟踪训练】新知探究2 . 如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.解:连接OM,过M作AB⊥OM,
交⊙O于A,B两点.AB课堂小结1.圆的相关概念,弦、弧、优弧、劣弧.2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧. 通过本课时的学习,需要我们掌握:规律方法:课堂小结 运用垂径定理及其推论解决一些数学问题.最常见的辅
助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂
线,构造直角三角形,利用勾股定理解决问题.课堂小测1. 如图,AB,AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,如果MN=3,那么BC=________.解析:由垂径定理得AN=CN,AM=BM,
所以BC=2MN=6.6课堂小测2. 如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.19 B.16 C.18 D.20D课堂小测B课堂小测4. 如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )?B课堂小测5.如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为( )
A.5cm B.2.5cm C.2cm D.1cmD
2.运用探索、推理,充分把握圆中的垂径定理及其逆定理.
3.拓展思维,与实践相结合,运用垂径定理及其逆定理进行
有关的计算和证明.新课导入情境引入点在圆外,这个点到圆心的距离大于半径 点在圆上,点在圆内,这个点到圆心的距离等于半径 这个点到圆心的距离小于半径 点与圆的位置关系新课导入2.它的对称轴是什么?是圆的对称轴是任意一条经过圆心的直线3.你能找到多少条对称轴?它有无数条对称轴.1.圆是轴对称图形吗?新知探究③AM=BM,AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.小明发现图中有:①CD是直径②CD⊥AB【问题】新知探究连接OA,OB,则OA=OB.●OCD └在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,理 由:M新知探究垂直于平分这条弦,并且平分弦所对的弧. 弦的直径在⊙O中,直径CD⊥弦AB,?定理:ABCDOM新知探究┗在⊙O中,直径CD平分弦AB,∴ CD⊥AB,平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.定理:新知探究弦(不是直径)并且平分弦所对的弧 . 平分的直径垂直于弦, 结论:新知探究1.在⊙O中,OC垂直于弦AB,AB = 8,
OA = 5,则AC= ,OC = .┏58432.在⊙O中,OC平分弦AB,AB = 16,
OA = 10,则∠OCA = °,
OC = .1610906【巩固练习】新知探究例1 . 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB .└新知探究解:连接OA,在⊙O中,直径CD⊥AB,∴ AB =2AM,△OMA是直角三角形.∵ CD = 20,∴ AO = CO = 10.∴ OM = OC – CM = 10 – 4 = 6.在Rt△OMA中,AO = 10,OM = 6,根据勾股定理,得:AO2=OM2+AM2,∴ AB = 2AM = 2 × 8 = 16.└?新知探究例2 . 如图,两个圆都以点O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上.你认为AC与BD的大小有什么关系?为什么?解 : 作OG⊥AB,
∵AG=BG,CG=DG,
∴AC=BD.G新知探究└解 : 连接OC.设弯路的半径为Rm,则OF=(R-90)m.根据勾股定理,得OC2=CF2+OF2,即解这个方程,得R=545,∴这段弯路的半径为545m .新知探究1.判断:
(1)垂直于弦的直线平分这条弦,并且平分弦所对的两
条弧. ( )
(2)平分弦所对的一条弧的直径一定平分这条弦所对
的另一条弧. ( )
(3)经过弦的中点的直径一定垂直于弦. ( )
(4)弦的垂直平分线一定平分这条弦所对的弧( )对错错对【跟踪训练】新知探究2 . 如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.解:连接OM,过M作AB⊥OM,
交⊙O于A,B两点.AB课堂小结1.圆的相关概念,弦、弧、优弧、劣弧.2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧. 通过本课时的学习,需要我们掌握:规律方法:课堂小结 运用垂径定理及其推论解决一些数学问题.最常见的辅
助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂
线,构造直角三角形,利用勾股定理解决问题.课堂小测1. 如图,AB,AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,如果MN=3,那么BC=________.解析:由垂径定理得AN=CN,AM=BM,
所以BC=2MN=6.6课堂小测2. 如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.19 B.16 C.18 D.20D课堂小测B课堂小测4. 如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )?B课堂小测5.如图,AB是⊙O的弦,半径OC⊥AB于D点,且AB=6cm,OD=4cm,则DC的长为( )
A.5cm B.2.5cm C.2cm D.1cmD
