北师大版数学九年级下册课件 2.1 二次函数(20张PPT)
文档属性
| 名称 | 北师大版数学九年级下册课件 2.1 二次函数(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-27 19:45:34 | ||
图片预览






文档简介
课件20张PPT。第二章
二次函数九年级数学北师版·下册2.1 二次函数教学目标1.探索并归纳二次函数的定义.(重点)
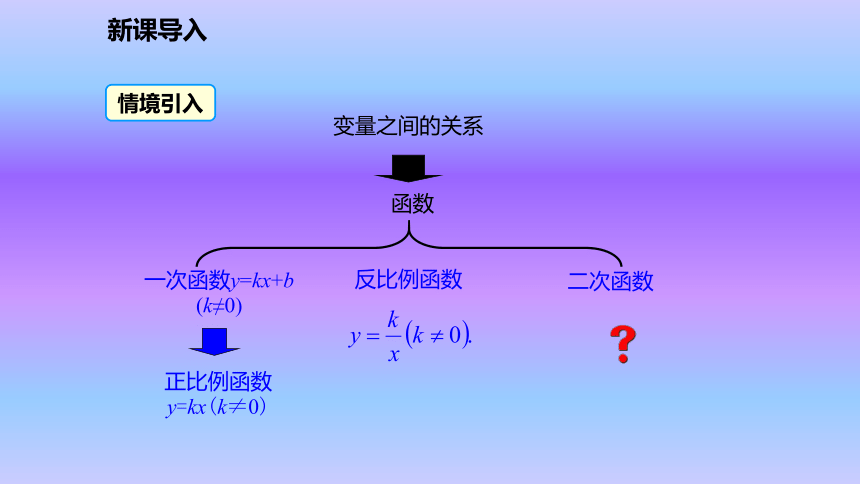
2.能够表示简单变量之间的二次函数关系.(难点)新课导入情境引入 函数变量之间的关系一次函数y=kx+b (k≠0)反比例函数二次函数正比例函数y=kx(k≠0) 某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
问题1:问题中有哪些变量?其中哪些是自变量?哪些是因变量?新知探究解:多种的橙子树的棵数和少结的橙子个数是变量.
其中多种的橙子树的棵数是自变量,
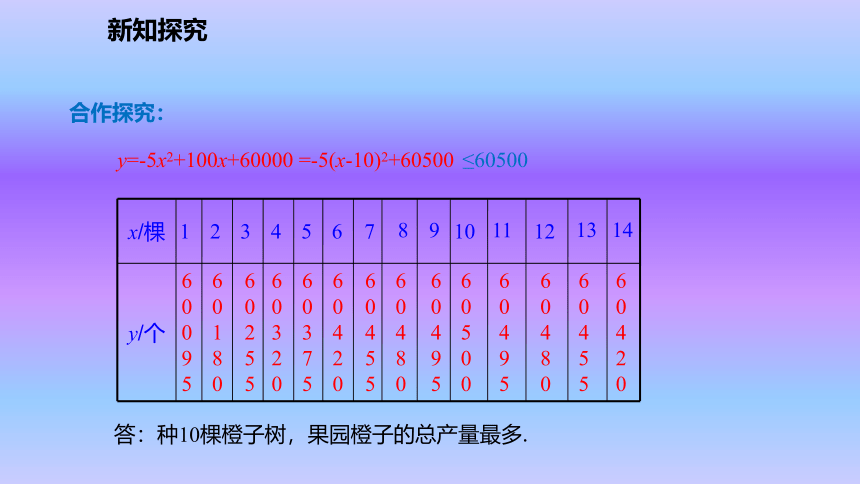
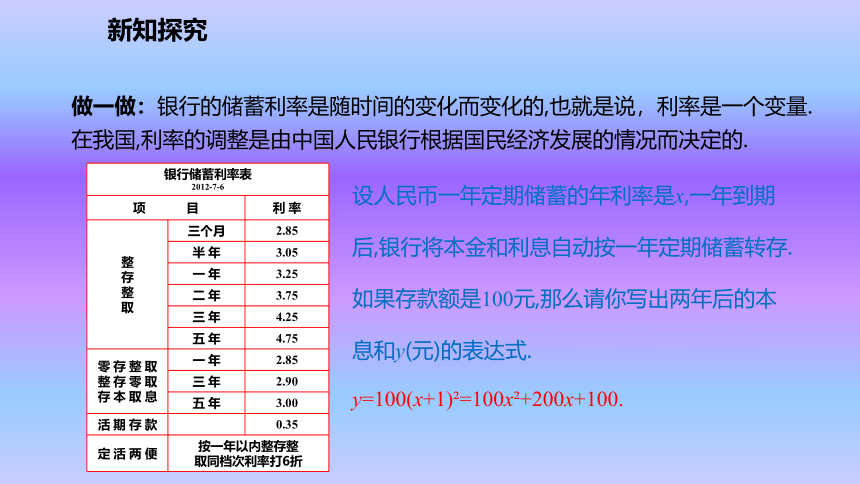
少结的橙子个数是因变量.新知探究新知探究解:果园共有(100+x)棵树,平均每棵树结(600-5x)个橙子. 解:y=(100+x)(600-5x) =-5x2+100x+60000. 问题3:如果果园橙子树的总产量为y个,那么请你写出y与x之间的关系式. 问题2:假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?新知探究在上述问题中,种多少棵橙子树,可以使果园橙子的总产量最多?y=-5(x2-20x)+60000=-5(x2-20x+102-102)+60000=-5(x-10)2+60500 解:想一想:新知探究123 45678910111213146009560180602556032060375604206045560480604956050060495604806045560420y=-5x2+100x+60000 =-5(x-10)2+60500合作探究:≤60500答:种10棵橙子树,果园橙子的总产量最多.新知探究做一做:银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的.设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款额是100元,那么请你写出两年后的本息和y(元)的表达式.y=100(x+1)2=100x2+200x+100.新知探究定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数,其中,ax2叫做二次项,a叫做二次项系数;bx叫做一次项, b叫做一次项系数;c叫做常数项.如: y=100 x2 + 200 x + 100abc新知探究1.下列函数中,哪些是二次函数?如果是二次函数请指出二次函数中a,b,c分别为多少?(1)y=3(x-1)2+1.(3)s=3-2t2.(5)y=(x+3)2-x2.(6)v=10πr2.(是)其中a=3,b=-6,c=4(不是)(是)其中a=-2,b=0,c=3(不是)(不是)(是)其中a=10π,b=c=0【跟踪训练】??新知探究2.用总长为60m的篱笆围成矩形场地,场地面积S(m2)与矩形一边长a(m)之间的关系是什么?是函数关系吗?是哪一种函数? 解:S=a( -a)=a(30-a)=30a-a2=-a2+30a . 是函数关系且为二次函数关系.新知探究3.已知函数y=(m2+m) xm2-2m+2
(1)当函数是二次函数时,求m的值.
(2)当函数是一次函数时,求m的值.是二次函数的条件是m2-2m+2=2且m2+m≠0.是一次函数的条件是m2-2m+2=1且m2+m≠0.新知探究解: (1)依题意,得m2-2m+2=2,
解得m=2或m=0.
又由m2+m≠0,解得m≠0且m≠-1.
因此m=2.
(2)依题意,得m2-2m+2=1,
解得m=1.又由m2+m≠0,
解得m≠0且m≠-1.
因此m=1.新知探究点拨: 判断一个函数是否是二次函数的“三步法”新知探究列二次函数表达式 4、某商场购进一种单价为40元的商品,如果以单价60元售出,那么每天可卖出300个,根据销售经验,每降价1元,每天可多卖出20个,假设每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数表达式.
(2)求出W与x的函数表达式(不必写出x的取值范围).销量=300+20×降价 总利润=销量×每个商品的利润y=300+20x.W=(300+20x)(60-40-x)=-20x2+100x+6000.新知探究点拨: 实际问题中建立二次函数表达式的“三步法”课堂小结1.定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
2.y=ax2+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax2(a≠0,b=0,c=0).
(2)y=ax2+c(a≠0,b=0,c≠0).
(3)y=ax2+bx (a≠0,b≠0,c=0).
3.定义的实质是:ax2+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.规律方法:1.关于x的二次函数表达式y=ax2+bx+c一定是整式,a,b,c为常数,且 a≠0.2.等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.课堂小测1. 某药店决定对某药品价格分两次降价,若设平均每次降价的百分率为x,该药品原价为18元,降价后的价格为y元,则y与x之间的函数关系式为 ,化作一般形式是 .y=18(1-x)2y=18x2-36x+18课堂小测 3.如果函数y=(k-3)xk2-3k+2+kx+1是二次函数,则k的值一定是______ . 02.如果函数y=xk2-3k+2+kx+1是二次函数,则k的值一定是______ . 0或3
2.能够表示简单变量之间的二次函数关系.(难点)新课导入情境引入 函数变量之间的关系一次函数y=kx+b (k≠0)反比例函数二次函数正比例函数y=kx(k≠0) 某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
问题1:问题中有哪些变量?其中哪些是自变量?哪些是因变量?新知探究解:多种的橙子树的棵数和少结的橙子个数是变量.
其中多种的橙子树的棵数是自变量,
少结的橙子个数是因变量.新知探究新知探究解:果园共有(100+x)棵树,平均每棵树结(600-5x)个橙子. 解:y=(100+x)(600-5x) =-5x2+100x+60000. 问题3:如果果园橙子树的总产量为y个,那么请你写出y与x之间的关系式. 问题2:假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?新知探究在上述问题中,种多少棵橙子树,可以使果园橙子的总产量最多?y=-5(x2-20x)+60000=-5(x2-20x+102-102)+60000=-5(x-10)2+60500 解:想一想:新知探究123 45678910111213146009560180602556032060375604206045560480604956050060495604806045560420y=-5x2+100x+60000 =-5(x-10)2+60500合作探究:≤60500答:种10棵橙子树,果园橙子的总产量最多.新知探究做一做:银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的.设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款额是100元,那么请你写出两年后的本息和y(元)的表达式.y=100(x+1)2=100x2+200x+100.新知探究定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数,其中,ax2叫做二次项,a叫做二次项系数;bx叫做一次项, b叫做一次项系数;c叫做常数项.如: y=100 x2 + 200 x + 100abc新知探究1.下列函数中,哪些是二次函数?如果是二次函数请指出二次函数中a,b,c分别为多少?(1)y=3(x-1)2+1.(3)s=3-2t2.(5)y=(x+3)2-x2.(6)v=10πr2.(是)其中a=3,b=-6,c=4(不是)(是)其中a=-2,b=0,c=3(不是)(不是)(是)其中a=10π,b=c=0【跟踪训练】??新知探究2.用总长为60m的篱笆围成矩形场地,场地面积S(m2)与矩形一边长a(m)之间的关系是什么?是函数关系吗?是哪一种函数? 解:S=a( -a)=a(30-a)=30a-a2=-a2+30a . 是函数关系且为二次函数关系.新知探究3.已知函数y=(m2+m) xm2-2m+2
(1)当函数是二次函数时,求m的值.
(2)当函数是一次函数时,求m的值.是二次函数的条件是m2-2m+2=2且m2+m≠0.是一次函数的条件是m2-2m+2=1且m2+m≠0.新知探究解: (1)依题意,得m2-2m+2=2,
解得m=2或m=0.
又由m2+m≠0,解得m≠0且m≠-1.
因此m=2.
(2)依题意,得m2-2m+2=1,
解得m=1.又由m2+m≠0,
解得m≠0且m≠-1.
因此m=1.新知探究点拨: 判断一个函数是否是二次函数的“三步法”新知探究列二次函数表达式 4、某商场购进一种单价为40元的商品,如果以单价60元售出,那么每天可卖出300个,根据销售经验,每降价1元,每天可多卖出20个,假设每个降价x(元),每天销售y(个),每天获得利润W(元).
(1)写出y与x的函数表达式.
(2)求出W与x的函数表达式(不必写出x的取值范围).销量=300+20×降价 总利润=销量×每个商品的利润y=300+20x.W=(300+20x)(60-40-x)=-20x2+100x+6000.新知探究点拨: 实际问题中建立二次函数表达式的“三步法”课堂小结1.定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
2.y=ax2+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax2(a≠0,b=0,c=0).
(2)y=ax2+c(a≠0,b=0,c≠0).
(3)y=ax2+bx (a≠0,b≠0,c=0).
3.定义的实质是:ax2+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.规律方法:1.关于x的二次函数表达式y=ax2+bx+c一定是整式,a,b,c为常数,且 a≠0.2.等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.课堂小测1. 某药店决定对某药品价格分两次降价,若设平均每次降价的百分率为x,该药品原价为18元,降价后的价格为y元,则y与x之间的函数关系式为 ,化作一般形式是 .y=18(1-x)2y=18x2-36x+18课堂小测 3.如果函数y=(k-3)xk2-3k+2+kx+1是二次函数,则k的值一定是______ . 02.如果函数y=xk2-3k+2+kx+1是二次函数,则k的值一定是______ . 0或3
