北师大版九年级数学下册:3.4圆周角和圆心角的关系 课件 (第2课时)(共24张PPT)
文档属性
| 名称 | 北师大版九年级数学下册:3.4圆周角和圆心角的关系 课件 (第2课时)(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览





文档简介
课件24张PPT。第三章
圆3.4.2 圆周角定理推论九年级数学北师版·下册教学目标1.掌握圆周角定理几个推论的内容,会熟练运用推论解决问题.
2.培养学生观察、分析及理解问题的能力.
3.在学生自主探索推论的过程中,经历猜想、推理、验证等环节,获
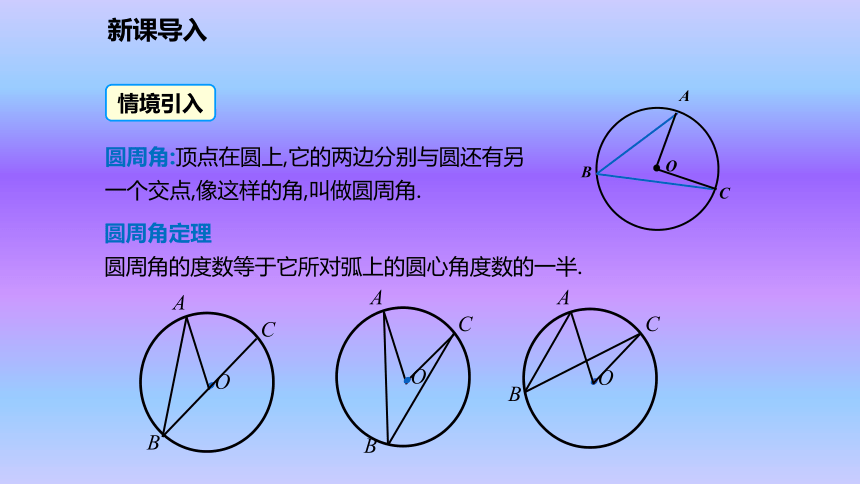
得正确的学习方式.新课导入情境引入圆周角:顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.圆周角定理
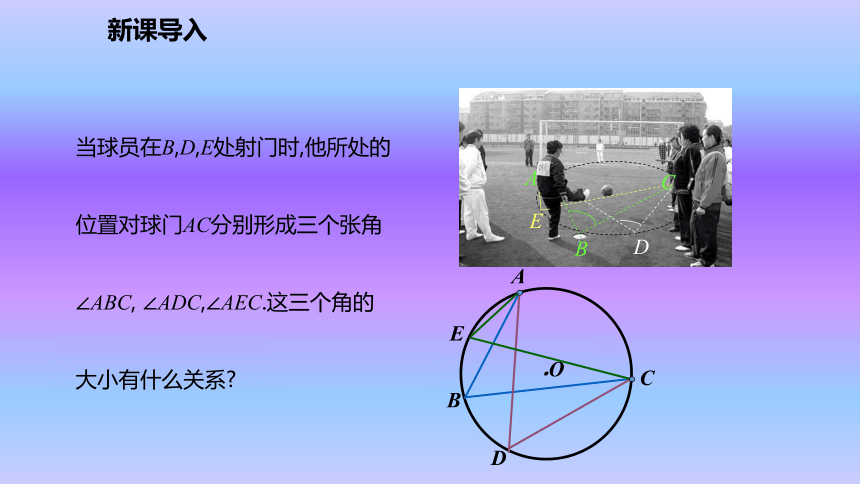
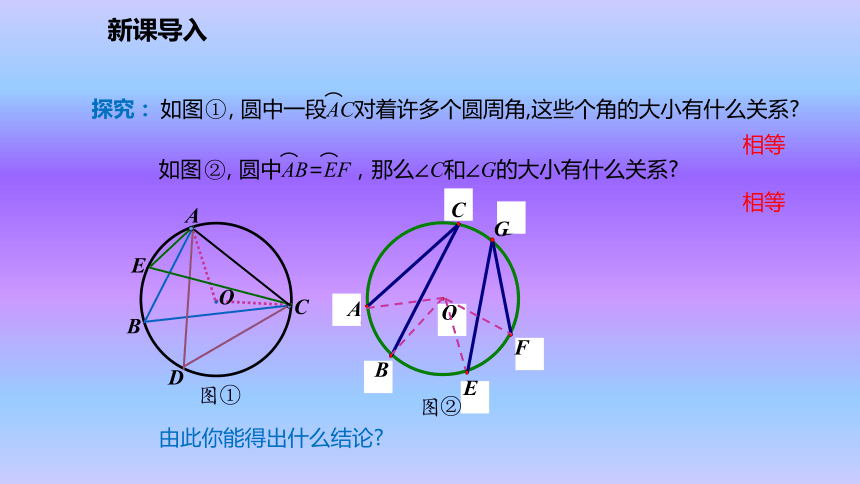
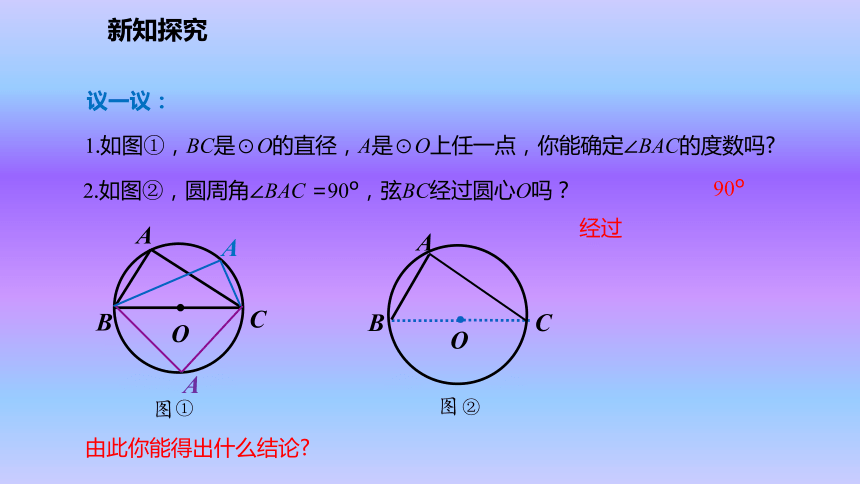
圆周角的度数等于它所对弧上的圆心角度数的一半.新课导入当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?新课导入由此你能得出什么结论?OABGFEC相等相等①②①②新知探究圆周角定理的推论1:同弧或等弧所对的圆周角相等.用于找相等的角新知探究1.如图①,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?2.如图②,圆周角∠BAC =90o,弦BC经过圆心O吗?由此你能得出什么结论?议一议:90o经过①②新知探究用于判断某条弦是否是直径用于构造直角圆周角定理的推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径.新知探究推论1 : 同弧或等弧所对的圆周角相等;推论2 : 直径所对的圆周角是直角;90°的圆周角所对的弦是直径 .圆周角定理的推论:新知探究例1 . 如图 , AB是⊙O的直径,BD是⊙O的弦 , 延长BD到C ,
使AC=AB , BD与CD的大小有什么关系 ? 为什么?解:BD=CD.
理由:如图,连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,
即AD⊥BC.
又∵AC=AB,∴BD=CD.新知探究证明:如图,连接AD,AE .
∴ AD=DB,AE=EC,
∠DAB=∠AED,∠EAC= ∠ADE,
∴ ∠AMN=∠ANM,∴AM=AN .
∴ △AMN为等腰三角形.新知探究√×××1.判断题:
(1)在同圆或等圆中等弧所对的圆周角相等. ( )
(2)相等的圆周角所对的弧也相等. ( )
(3)90°的角所对的弦是直径. ( )
(4)同弦所对的圆周角相等. ( )(3)【跟踪训练】新知探究2.填空题:
(1)如图所示,∠BAC= ,∠DAC= .∠DBC∠BDC(2)如图所示,⊙O的直径AB=10cm,C为⊙O上一点,∠BAC=30°,则BC= cm. 5新知探究3 . 如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD
交⊙O1于C,则
(1)OC与AD的位置关系是__________________;
(2)OC与BD的位置关系是___________;
(3)若OC=2cm,则BD=______cm.OC垂直平分AD平行4CABO新知探究4.如图,△ABC的顶点均在⊙O上, AB=4, ∠C=30°,求⊙O的直径. E解:连接AO并延长交⊙O于点E,
连接BE所以∠E=30°, ∠ABE=90°.
由AB=4得直径AE=8.新知探究5 . 如图,AE是⊙O的直径, △ABC的顶点都在⊙O上,AD是△ABC的高.
求证:AB·AC=AE·AD.AOBCDE?新知探究定 理: 圆的内接四边形的对角互补 定理拓展: 任何一个外角都等于它的内对角 .∠D+∠B=180°
∠A+∠C=180°∠EAB=∠BCD
∠FCB=∠BAD 对 角 外 角 内 对 角新知探究如图,⊙O1和⊙O2都经过A、B两点,经过A点的直线CD与⊙O1交于点C,
与⊙O2交于点D,经过B点的直线EF与⊙O1交于点E,与⊙O2交于点F .
求证:CE∥DF .有两个圆的题目常用的一种辅助线:作公共弦.
此图形是一个考试热门图形.又一种重要的辅助线新知探究证明:连接AB, ∵四边形ABEC是⊙O1的内接四边形, 可得∠BAD=∠E. 又∵四边形ABFD是⊙O2的内接四边形, ∴∠BAD+∠F=180°, ∴∠E+∠F=180°, ∴CE∥DF.新知探究135°25【跟踪训练】1.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:
(1)构造直径上的圆周角.
(2)构造同弧所对的圆周角.
2.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周
角也是常用方法之一.课堂小结推论1 : 同弧或等弧所对的圆周角相等;推论2 : 直径所对的圆周角是直角;90°的圆周角所对的弦是直径 .圆周角定理的推论:圆的内接四边形的对角互补 . 任何一个外角都等于它的内对角 .拓展:课堂小结【规律方法】 圆周角定理建立了圆心角与圆周角的关系,而同圆或
等圆中圆心角、弧、弦之间又存在等量关系,因此,圆中
的角(圆周角和圆心角)、弦、弧等的相等关系可以互相
转化.但转化过程中要注意以圆心角、弧为桥梁.如由弦相等
只能得弧或圆心角相等,不能直接得圆周角相等.课堂小测?D 课堂小测?B
2.培养学生观察、分析及理解问题的能力.
3.在学生自主探索推论的过程中,经历猜想、推理、验证等环节,获
得正确的学习方式.新课导入情境引入圆周角:顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.圆周角定理
圆周角的度数等于它所对弧上的圆心角度数的一半.新课导入当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?新课导入由此你能得出什么结论?OABGFEC相等相等①②①②新知探究圆周角定理的推论1:同弧或等弧所对的圆周角相等.用于找相等的角新知探究1.如图①,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?2.如图②,圆周角∠BAC =90o,弦BC经过圆心O吗?由此你能得出什么结论?议一议:90o经过①②新知探究用于判断某条弦是否是直径用于构造直角圆周角定理的推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径.新知探究推论1 : 同弧或等弧所对的圆周角相等;推论2 : 直径所对的圆周角是直角;90°的圆周角所对的弦是直径 .圆周角定理的推论:新知探究例1 . 如图 , AB是⊙O的直径,BD是⊙O的弦 , 延长BD到C ,
使AC=AB , BD与CD的大小有什么关系 ? 为什么?解:BD=CD.
理由:如图,连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,
即AD⊥BC.
又∵AC=AB,∴BD=CD.新知探究证明:如图,连接AD,AE .
∴ AD=DB,AE=EC,
∠DAB=∠AED,∠EAC= ∠ADE,
∴ ∠AMN=∠ANM,∴AM=AN .
∴ △AMN为等腰三角形.新知探究√×××1.判断题:
(1)在同圆或等圆中等弧所对的圆周角相等. ( )
(2)相等的圆周角所对的弧也相等. ( )
(3)90°的角所对的弦是直径. ( )
(4)同弦所对的圆周角相等. ( )(3)【跟踪训练】新知探究2.填空题:
(1)如图所示,∠BAC= ,∠DAC= .∠DBC∠BDC(2)如图所示,⊙O的直径AB=10cm,C为⊙O上一点,∠BAC=30°,则BC= cm. 5新知探究3 . 如图,以⊙O的半径OA为直径作⊙O1,⊙O的弦AD
交⊙O1于C,则
(1)OC与AD的位置关系是__________________;
(2)OC与BD的位置关系是___________;
(3)若OC=2cm,则BD=______cm.OC垂直平分AD平行4CABO新知探究4.如图,△ABC的顶点均在⊙O上, AB=4, ∠C=30°,求⊙O的直径. E解:连接AO并延长交⊙O于点E,
连接BE所以∠E=30°, ∠ABE=90°.
由AB=4得直径AE=8.新知探究5 . 如图,AE是⊙O的直径, △ABC的顶点都在⊙O上,AD是△ABC的高.
求证:AB·AC=AE·AD.AOBCDE?新知探究定 理: 圆的内接四边形的对角互补 定理拓展: 任何一个外角都等于它的内对角 .∠D+∠B=180°
∠A+∠C=180°∠EAB=∠BCD
∠FCB=∠BAD 对 角 外 角 内 对 角新知探究如图,⊙O1和⊙O2都经过A、B两点,经过A点的直线CD与⊙O1交于点C,
与⊙O2交于点D,经过B点的直线EF与⊙O1交于点E,与⊙O2交于点F .
求证:CE∥DF .有两个圆的题目常用的一种辅助线:作公共弦.
此图形是一个考试热门图形.又一种重要的辅助线新知探究证明:连接AB, ∵四边形ABEC是⊙O1的内接四边形, 可得∠BAD=∠E. 又∵四边形ABFD是⊙O2的内接四边形, ∴∠BAD+∠F=180°, ∴∠E+∠F=180°, ∴CE∥DF.新知探究135°25【跟踪训练】1.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:
(1)构造直径上的圆周角.
(2)构造同弧所对的圆周角.
2.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周
角也是常用方法之一.课堂小结推论1 : 同弧或等弧所对的圆周角相等;推论2 : 直径所对的圆周角是直角;90°的圆周角所对的弦是直径 .圆周角定理的推论:圆的内接四边形的对角互补 . 任何一个外角都等于它的内对角 .拓展:课堂小结【规律方法】 圆周角定理建立了圆心角与圆周角的关系,而同圆或
等圆中圆心角、弧、弦之间又存在等量关系,因此,圆中
的角(圆周角和圆心角)、弦、弧等的相等关系可以互相
转化.但转化过程中要注意以圆心角、弧为桥梁.如由弦相等
只能得弧或圆心角相等,不能直接得圆周角相等.课堂小测?D 课堂小测?B
