五年级数学下册课件 - 探索图形 -人教新课标(共18张PPT)
文档属性
| 名称 | 五年级数学下册课件 - 探索图形 -人教新课标(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 823.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 11:46:01 | ||
图片预览



文档简介
(共18张PPT)
人教版五年级数学下册
探索图形
6个面
8个顶点
12条棱
3x3x3=27(个)
6个面
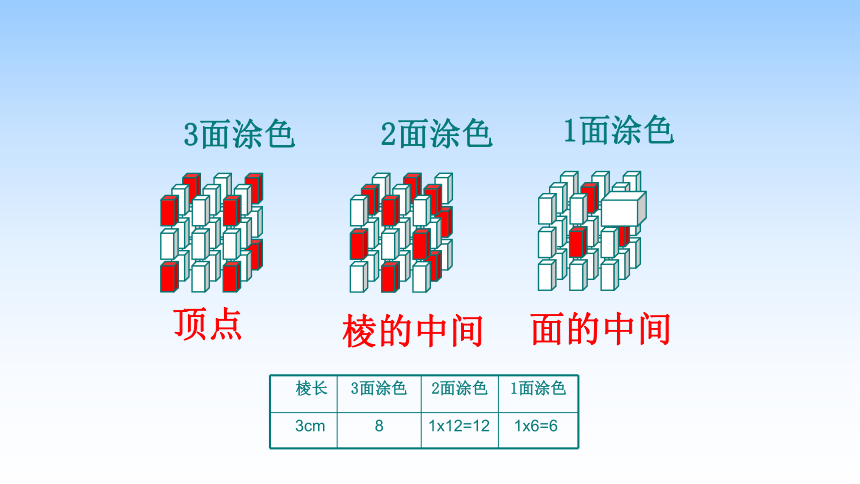
3面涂色
顶点
2面涂色
棱的中间
1面涂色
面的中间
棱长 3面涂色 2面涂色 1面涂色
3cm
8
1x12=12
1x6=6
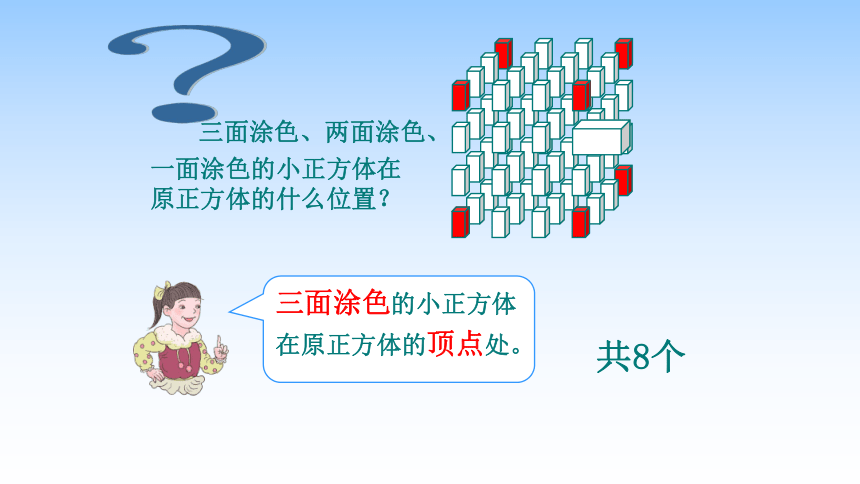
三面涂色的小正方体在原正方体的顶点处。
三面涂色、两面涂色、一面涂色的小正方体在原正方体的什么位置?
?
共8个
两面涂色的小正方体在原正方体每条棱的中间
共2x12=24(个)
一面涂色的小正方体在原正方体每个面中间位置。
共4x6=24(个)
观察填出的表格,你能发现什么规律?
棱长 3面涂色 2面涂色 1面涂色
3cm 8 1x12=12 1x6=6
4cm 8 2x12=24 2x6=12
三面涂色
三面涂色的小正方体都在大正方体的顶点的位置。不论棱长是几,分割后三面涂色的小正方体的个数都是8个。
两面涂色
两面涂色的小正方体都在大正方体的棱的位置,只要用每条棱中间两面涂色的小正方体的个数乘12,就得出两面涂色的小正方体的总个数。
一面涂色
一面涂色的小正方体都在大正方体的面的位置,只要用每个面上一面涂色的小正方体的个数乘6,就得出一面涂色的小正方体的总个数。
根据发现的规律,你知道棱长是5厘米的大正方体表面的涂色情况是怎样的?试着填一填。
棱长 3面涂色 2面涂色 1面涂色
3cm 8 1x12=12 1x6=6
4cm 8 2x12=24 4x6=24
3x12=36
5cm
8
9x6=54
没有涂色的小正方体有着怎样的规律呢?
?
棱长 3 4 5
没有涂色的个数
33
23
13
33=27
23=8
13=1
1
8
27
…
…
巩固练习
如果摆成下面的几何体,你会数吗?
4
10
20
绿色圃中小学教育网 http://www.Lspjy.com
结语
当我们遇到比较复杂的问题,解决起来有困难时,可以先尝试从简单的情况,看能否发现规律,再应用规律去解决复杂的问题,这是一种解决问题常用的思想方法。
人教版五年级数学下册
探索图形
6个面
8个顶点
12条棱
3x3x3=27(个)
6个面
3面涂色
顶点
2面涂色
棱的中间
1面涂色
面的中间
棱长 3面涂色 2面涂色 1面涂色
3cm
8
1x12=12
1x6=6
三面涂色的小正方体在原正方体的顶点处。
三面涂色、两面涂色、一面涂色的小正方体在原正方体的什么位置?
?
共8个
两面涂色的小正方体在原正方体每条棱的中间
共2x12=24(个)
一面涂色的小正方体在原正方体每个面中间位置。
共4x6=24(个)
观察填出的表格,你能发现什么规律?
棱长 3面涂色 2面涂色 1面涂色
3cm 8 1x12=12 1x6=6
4cm 8 2x12=24 2x6=12
三面涂色
三面涂色的小正方体都在大正方体的顶点的位置。不论棱长是几,分割后三面涂色的小正方体的个数都是8个。
两面涂色
两面涂色的小正方体都在大正方体的棱的位置,只要用每条棱中间两面涂色的小正方体的个数乘12,就得出两面涂色的小正方体的总个数。
一面涂色
一面涂色的小正方体都在大正方体的面的位置,只要用每个面上一面涂色的小正方体的个数乘6,就得出一面涂色的小正方体的总个数。
根据发现的规律,你知道棱长是5厘米的大正方体表面的涂色情况是怎样的?试着填一填。
棱长 3面涂色 2面涂色 1面涂色
3cm 8 1x12=12 1x6=6
4cm 8 2x12=24 4x6=24
3x12=36
5cm
8
9x6=54
没有涂色的小正方体有着怎样的规律呢?
?
棱长 3 4 5
没有涂色的个数
33
23
13
33=27
23=8
13=1
1
8
27
…
…
巩固练习
如果摆成下面的几何体,你会数吗?
4
10
20
绿色圃中小学教育网 http://www.Lspjy.com
结语
当我们遇到比较复杂的问题,解决起来有困难时,可以先尝试从简单的情况,看能否发现规律,再应用规律去解决复杂的问题,这是一种解决问题常用的思想方法。
