【全国百强校】浙江省萧山中学人教版高中数学必修一复习课件:3.1函数的概念及表示法 (共24张PPT)
文档属性
| 名称 | 【全国百强校】浙江省萧山中学人教版高中数学必修一复习课件:3.1函数的概念及表示法 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 20:20:01 | ||
图片预览







文档简介
(共24张PPT)
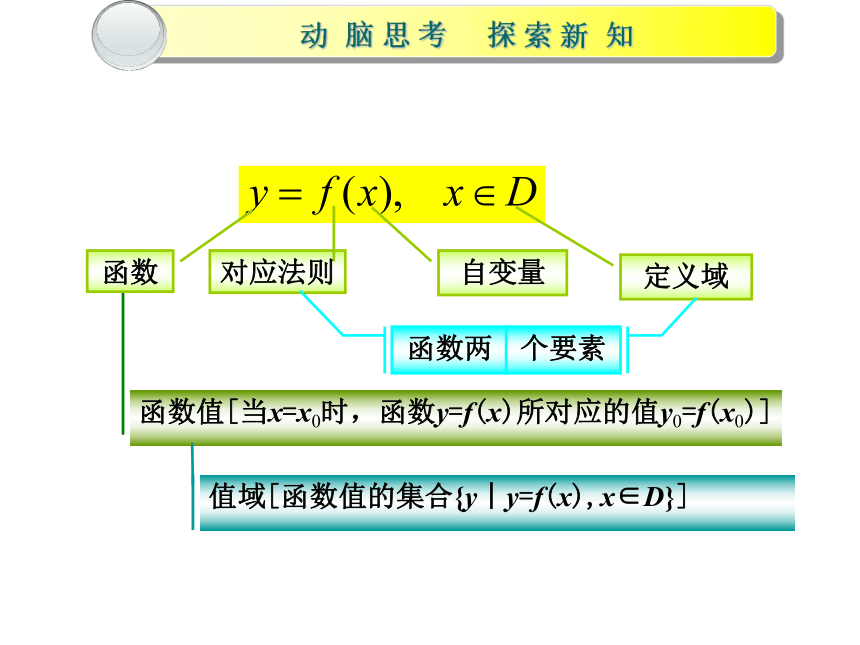
函数的概念及表示法
在某一个变化过程中有两个变量x和y,设变量x的取值范围
为数集D,如果对于D内的每一个x值,按照某个对应法则f,
y都有唯一确定的值与它对应,那么,把x叫做自变量,把
y叫做x的函数.
函数
对应法则
自变量
定义域
函数值[当x=x0时,函数y=f(x)所对应的值y0=f(x0)]
值域[函数值的集合{y︱y=f(x),x∈D}]
分析 如果函数的对应法则是用代数式表示的,那么函数
的定义域就是使得代数式有意义的自变量的取值集合.
分析 本题是求自变量x=x0时对应的函数值,方法是将x0代入
到函数表达式中求值.
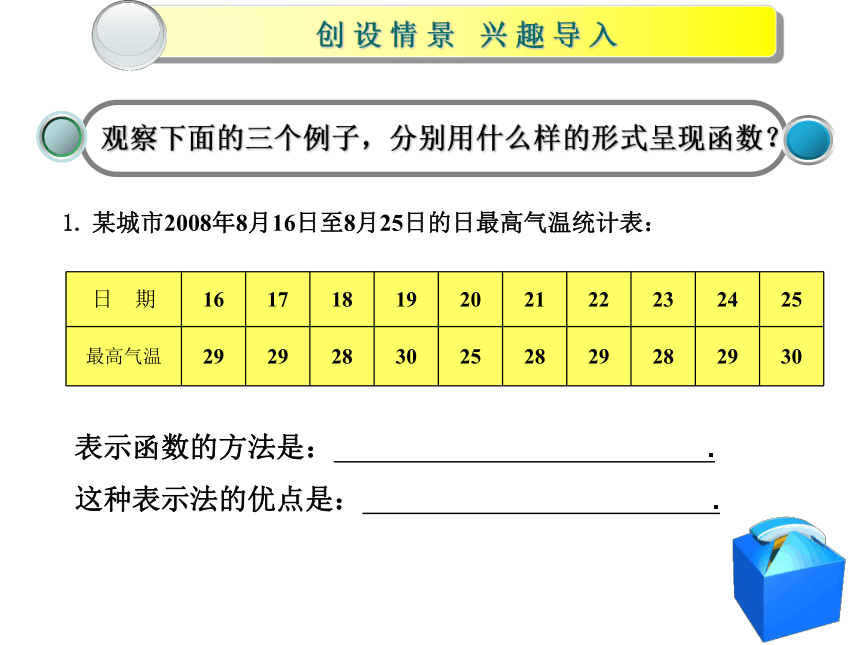
1. 某城市2008年8月16日至8月25日的日最高气温统计表:
表示函数的方法是: .
这种表示法的优点是: .
日 期 16 17 18 19 20 21 22 23 24 25
最高气温 29 29 28 30 25 28 29 28 29 30
2. 某市温度自动记录仪记录的气温时段图:
表示函数的方法是: .
这种表示法的优点是: .
3.用 S 来表示半径为r的圆的面积,则S=πr2.这个公式清楚地反映了
半径r与圆的面积S之间的函数关系,这里函数的定义域为R+.
表示函数的方法是: .
这种表示法的优点是: .
.
下面的表格是某商家销售计算机的统计表,你能从表格中得到哪些信息?
??类似的,在生活中你还见过哪些表格?
季? 度 第一季度 第二季度 第三季度 第四季度
数量(台) 400 405 632 605
.
??类似的,在生活中你还见过哪些图像?
下面是某商店一年的销售额随季度的变化曲线,你能从表格中得到哪些信息? ??
.
在匀速直线运动中,位移与时间之间有确定的依赖关系,
比如当速度为5m/s时,位移s=5t.
正方形的周长C和边长a之间也有类似的依赖关系,
能写出它们的函数关系式吗?
.
例3 文具店内出售某种铅笔,每支售价为0.12元,应付款额是购买铅
笔数的函数,当购买6支以内(含6支)的铅笔时,请用三种方法表示
这个函数.
解 (1)依照售价,分别计算出购买1-6支铅笔所需款数,
列成下面的表格,即为函数的列表法表示.
x(支) 1 2 3 4 5 6
y(元)
.
解 (2)以上表中的x值为横坐标,对应的y值为纵坐标,在直角
坐标系中依次作出点(1 , 0.12)、(2 , 0.24)、(3 , 0.36)、
(4,0.48)、(5,0.6)、(6,0.72),则函数的图像法表示如图所示.
例3 文具店内出售某种铅笔,每支售价为0.12元,应付款额是购买铅
笔数的函数,当购买6支以内(含6支)的铅笔时,请用三种方法表示
这个函数.
.
解 (3)关系式y=0.12 x就是函数的解析式,
故函数的解析法表示为
y=0.12 x, x ∈{1,2,3,4,5,6}
总结演示
例3 文具店内出售某种铅笔,每支售价为0.12元,应付款额是购买铅
笔数的函数,当购买6支以内(含6支)的铅笔时,请用三种方法表示
这个函数.
.
分析 按照“描点法”的步骤进行.
演 示
.
再 见
函数的概念及表示法
在某一个变化过程中有两个变量x和y,设变量x的取值范围
为数集D,如果对于D内的每一个x值,按照某个对应法则f,
y都有唯一确定的值与它对应,那么,把x叫做自变量,把
y叫做x的函数.
函数
对应法则
自变量
定义域
函数值[当x=x0时,函数y=f(x)所对应的值y0=f(x0)]
值域[函数值的集合{y︱y=f(x),x∈D}]
分析 如果函数的对应法则是用代数式表示的,那么函数
的定义域就是使得代数式有意义的自变量的取值集合.
分析 本题是求自变量x=x0时对应的函数值,方法是将x0代入
到函数表达式中求值.
1. 某城市2008年8月16日至8月25日的日最高气温统计表:
表示函数的方法是: .
这种表示法的优点是: .
日 期 16 17 18 19 20 21 22 23 24 25
最高气温 29 29 28 30 25 28 29 28 29 30
2. 某市温度自动记录仪记录的气温时段图:
表示函数的方法是: .
这种表示法的优点是: .
3.用 S 来表示半径为r的圆的面积,则S=πr2.这个公式清楚地反映了
半径r与圆的面积S之间的函数关系,这里函数的定义域为R+.
表示函数的方法是: .
这种表示法的优点是: .
.
下面的表格是某商家销售计算机的统计表,你能从表格中得到哪些信息?
??类似的,在生活中你还见过哪些表格?
季? 度 第一季度 第二季度 第三季度 第四季度
数量(台) 400 405 632 605
.
??类似的,在生活中你还见过哪些图像?
下面是某商店一年的销售额随季度的变化曲线,你能从表格中得到哪些信息? ??
.
在匀速直线运动中,位移与时间之间有确定的依赖关系,
比如当速度为5m/s时,位移s=5t.
正方形的周长C和边长a之间也有类似的依赖关系,
能写出它们的函数关系式吗?
.
例3 文具店内出售某种铅笔,每支售价为0.12元,应付款额是购买铅
笔数的函数,当购买6支以内(含6支)的铅笔时,请用三种方法表示
这个函数.
解 (1)依照售价,分别计算出购买1-6支铅笔所需款数,
列成下面的表格,即为函数的列表法表示.
x(支) 1 2 3 4 5 6
y(元)
.
解 (2)以上表中的x值为横坐标,对应的y值为纵坐标,在直角
坐标系中依次作出点(1 , 0.12)、(2 , 0.24)、(3 , 0.36)、
(4,0.48)、(5,0.6)、(6,0.72),则函数的图像法表示如图所示.
例3 文具店内出售某种铅笔,每支售价为0.12元,应付款额是购买铅
笔数的函数,当购买6支以内(含6支)的铅笔时,请用三种方法表示
这个函数.
.
解 (3)关系式y=0.12 x就是函数的解析式,
故函数的解析法表示为
y=0.12 x, x ∈{1,2,3,4,5,6}
总结演示
例3 文具店内出售某种铅笔,每支售价为0.12元,应付款额是购买铅
笔数的函数,当购买6支以内(含6支)的铅笔时,请用三种方法表示
这个函数.
.
分析 按照“描点法”的步骤进行.
演 示
.
再 见
