第二十二章 四边形 复习课件(19张)
文档属性
| 名称 | 第二十二章 四边形 复习课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 456.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 16:19:19 | ||
图片预览




文档简介
课件19张PPT。四边形复习由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形多边形内角和定理:
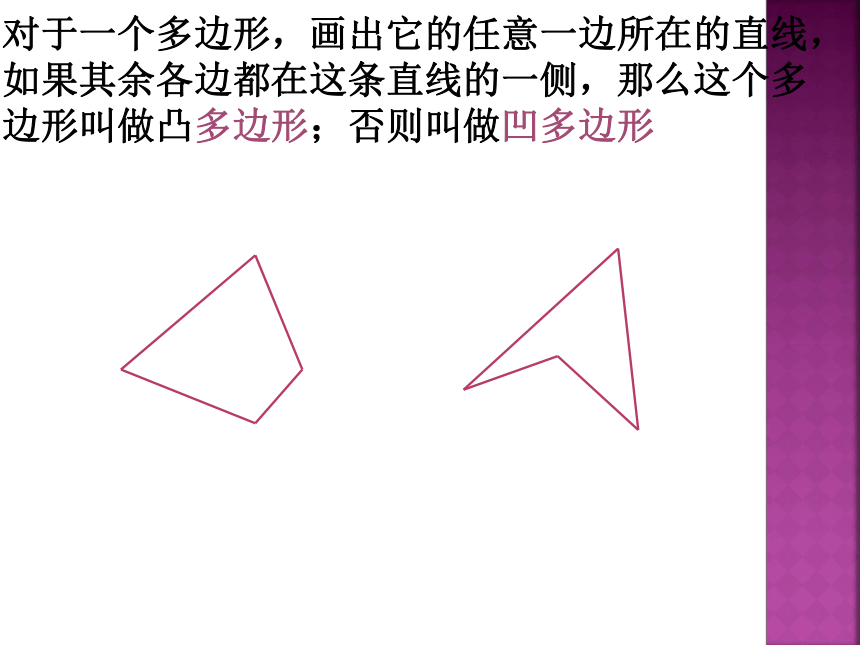
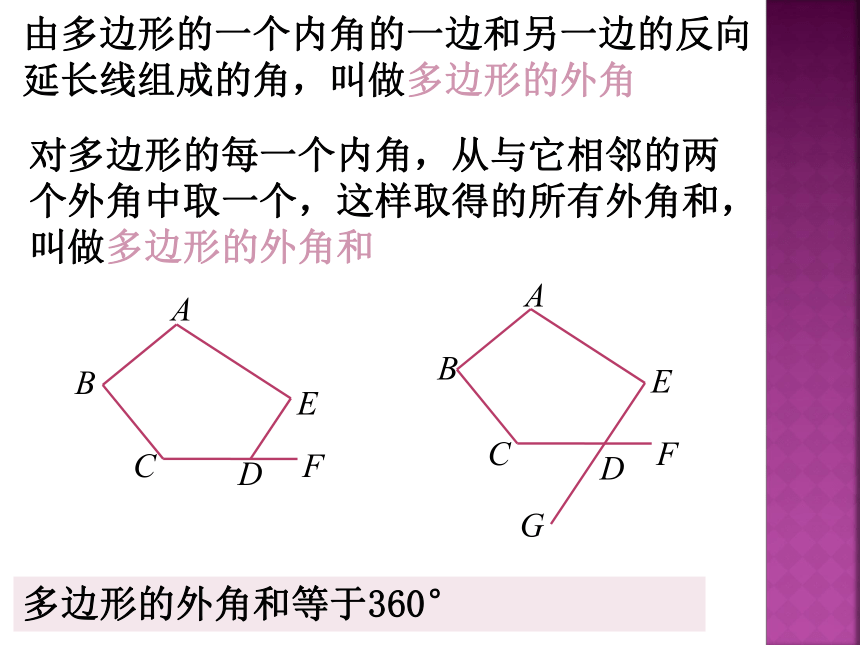
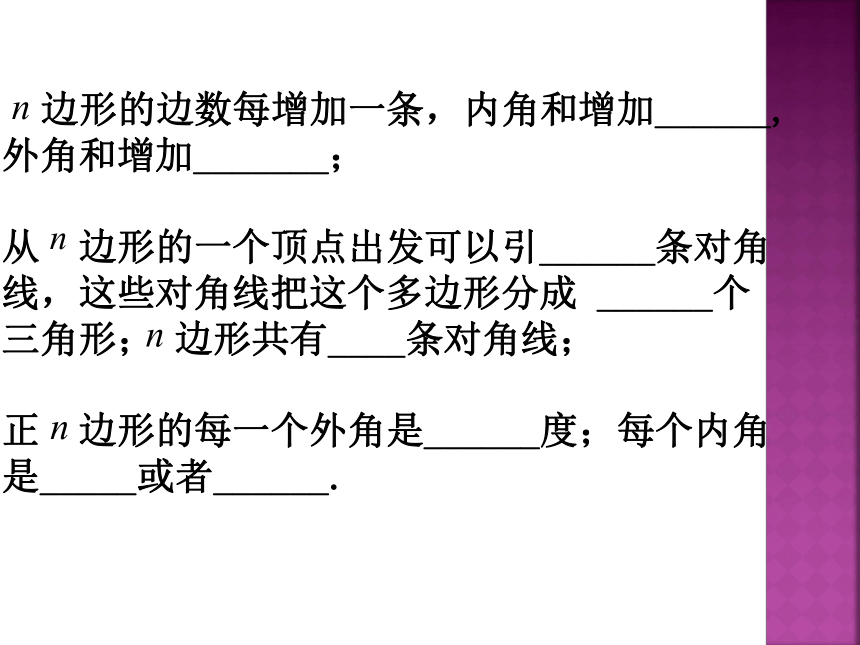
n边形的内角和等于(n-2)·180°.对于一个多边形,画出它的任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫做凸多边形;否则叫做凹多边形由多边形的一个内角的一边和另一边的反向延长线组成的角,叫做多边形的外角对多边形的每一个内角,从与它相邻的两个外角中取一个,这样取得的所有外角和,叫做多边形的外角和多边形的外角和等于360° 边形的边数每增加一条,内角和增加______,外角和增加_______;
从 边形的一个顶点出发可以引______条对角线,这些对角线把这个多边形分成 ______个三角形; 边形共有____条对角线;
正 边形的每一个外角是______度;每个内角是_____或者______. 夹在两条平行线之间的平行线段相等平行四边形的性质:性质定理1:平行四边形的对边相等性质定理2:平行四边形的对角相等性质定理3:平行四边形的两条对角线互相平分性质定理4:平行四边形是中心对称图形,对称中心是两条对角线的交点判定1:两组对边分别相等的四边形是平行四边形判定2:一组对边平行且相等的四边形是平行四边形平行四边形的判定:判定3:对角线互相平分的四边形是平行四边形判定4:两组对角分别相等的四边形是平行四边形有一个角是直角的平行四边形叫做矩形有一组邻边相等的平行四边形叫做菱形矩形的性质:矩形的性质定理1:矩形的四个角都是直角菱形的性质定理1:菱形的四条边都相等菱形的性质:矩形的性质定理2:矩形的两条对角线相等菱形的性质定理2:菱形的对角线互相垂直,并且每一条对角线平分一组对角平行四边形是中心对称图形矩形和菱形都是中心对称图形,它们是轴对称图形吗?矩形和菱形都是轴对称图形,它们分别有两条对称轴正方形的性质定理1:正方形的四个角都是直角,四条边都相等正方形的性质定理2:正方形的两条对角线相等,并且互相垂直,每条对角线平分一组对角有一组邻边相等并且有一个角是直角的平行四边形是正方形正方形的性质:一组对边平行而另一组对边不平行的四边形叫做梯形在梯形中,平行的两边叫做梯形的底(通常把较短的底叫做上底,较长的底叫做下底);不平行的两边叫做梯形的腰;两底之间的距离叫做梯形的高有一个角是直角的梯形叫做直角梯形两腰相等的梯形叫做等腰梯形等腰梯形性质定理1:等腰梯形在同一底上的两个内角相等等腰梯形性质定理2:等腰梯形的对角线相等等腰梯形判定定理1:在同一底上的两个内角相等的梯形是等腰梯形等腰梯形判定定理2:对角线相等的梯形是等腰梯形等腰梯形的性质:等腰梯形的判定:几种常见的添辅助线的方法:平移一腰作两条高延长两腰以一腰中点为对称中心,得全等三角形平移一条对角线作梯形中位线并联结一条对角线 三角形的中位线平行于第三边,并且等于第三边的一半 联结三角形两边中点的线段叫做三角形的中位线
三角形中位线:1、梯形中位线: 联结梯形两腰的中点的线段叫做梯形的中位线2、梯形中位线定理: 梯形的中位线平行于两底,并且等于两底和的一半知识结构应用2.对角线 的平行四边形是矩形.
3.菱形两条对角线长分别为4厘米和8厘米,则菱形的边长为 厘米. 归纳本章知识
从四边形:
从中位线:
从平面向量:小结
n边形的内角和等于(n-2)·180°.对于一个多边形,画出它的任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫做凸多边形;否则叫做凹多边形由多边形的一个内角的一边和另一边的反向延长线组成的角,叫做多边形的外角对多边形的每一个内角,从与它相邻的两个外角中取一个,这样取得的所有外角和,叫做多边形的外角和多边形的外角和等于360° 边形的边数每增加一条,内角和增加______,外角和增加_______;
从 边形的一个顶点出发可以引______条对角线,这些对角线把这个多边形分成 ______个三角形; 边形共有____条对角线;
正 边形的每一个外角是______度;每个内角是_____或者______. 夹在两条平行线之间的平行线段相等平行四边形的性质:性质定理1:平行四边形的对边相等性质定理2:平行四边形的对角相等性质定理3:平行四边形的两条对角线互相平分性质定理4:平行四边形是中心对称图形,对称中心是两条对角线的交点判定1:两组对边分别相等的四边形是平行四边形判定2:一组对边平行且相等的四边形是平行四边形平行四边形的判定:判定3:对角线互相平分的四边形是平行四边形判定4:两组对角分别相等的四边形是平行四边形有一个角是直角的平行四边形叫做矩形有一组邻边相等的平行四边形叫做菱形矩形的性质:矩形的性质定理1:矩形的四个角都是直角菱形的性质定理1:菱形的四条边都相等菱形的性质:矩形的性质定理2:矩形的两条对角线相等菱形的性质定理2:菱形的对角线互相垂直,并且每一条对角线平分一组对角平行四边形是中心对称图形矩形和菱形都是中心对称图形,它们是轴对称图形吗?矩形和菱形都是轴对称图形,它们分别有两条对称轴正方形的性质定理1:正方形的四个角都是直角,四条边都相等正方形的性质定理2:正方形的两条对角线相等,并且互相垂直,每条对角线平分一组对角有一组邻边相等并且有一个角是直角的平行四边形是正方形正方形的性质:一组对边平行而另一组对边不平行的四边形叫做梯形在梯形中,平行的两边叫做梯形的底(通常把较短的底叫做上底,较长的底叫做下底);不平行的两边叫做梯形的腰;两底之间的距离叫做梯形的高有一个角是直角的梯形叫做直角梯形两腰相等的梯形叫做等腰梯形等腰梯形性质定理1:等腰梯形在同一底上的两个内角相等等腰梯形性质定理2:等腰梯形的对角线相等等腰梯形判定定理1:在同一底上的两个内角相等的梯形是等腰梯形等腰梯形判定定理2:对角线相等的梯形是等腰梯形等腰梯形的性质:等腰梯形的判定:几种常见的添辅助线的方法:平移一腰作两条高延长两腰以一腰中点为对称中心,得全等三角形平移一条对角线作梯形中位线并联结一条对角线 三角形的中位线平行于第三边,并且等于第三边的一半 联结三角形两边中点的线段叫做三角形的中位线
三角形中位线:1、梯形中位线: 联结梯形两腰的中点的线段叫做梯形的中位线2、梯形中位线定理: 梯形的中位线平行于两底,并且等于两底和的一半知识结构应用2.对角线 的平行四边形是矩形.
3.菱形两条对角线长分别为4厘米和8厘米,则菱形的边长为 厘米. 归纳本章知识
从四边形:
从中位线:
从平面向量:小结
