人教版七年级数学下册7.1平面直角坐标系 教案(2课时)
文档属性
| 名称 | 人教版七年级数学下册7.1平面直角坐标系 教案(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 425.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览


文档简介
第七章 平面直角坐标系
7.1 平面直角坐标系
第1课时 有序数对
1.会用有序数对表示物体的位置.
2.结合用有序数对表示物体的位置的内容,体会数形结合的思想.
理解有序数对是怎样确定物体的位置的.
确定用怎样一对有顺序的数表示物体的位置.
一、创设情景 明确目标
在建国60周年的庆典活动中,天安门广场上出现了的背景图案,你知道它是怎么组成的吗?
二、自主学习 指向目标
自学教材第64页至65页,2.请完成学生用书部分.
1.我们把有顺序的两个数a和b组成的数对,叫做__有序数对__,记做__(a,b)__.
2.数对(a,b)和(b,a)是同一数对吗?答:__不是__.
3.在生活中常用__有序数对__、__方位角和距离__、__经纬度__等方法确定一个物体的位置.
4.下列数据不能确定物体位置的是( B )
A.5楼5号房间 B.北偏东36°
C.长征路98号 D.东经110°,北纬50°
三、合作探究 达成目标
●一 有序数对的概念
活动1:
阅读教材第64至65页,思考:
(1)同学们都有去影剧院看电影的经历,你是怎么找到自己的座位的?
(2)你若发现一本书某页有一处错误,怎样告诉其他同学这一处的位置?
(3)下图为教室的平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,5),(2,4),(4,2),(3,3),(5,6).
(4)所设在问题3中约定“列数在前,排数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?
(5)怎样确定教室里座位的位置?列数和排数的先后顺序对位置有影响吗?
(6)假设我们约定“列数在前,排数在后”,请你在图中标出上述同学的位置.
(7)你所标的(2,4),(4,2)是同一个位置吗?
展示点评:在教室里,排数与列数的先后顺序没有约定的情况下,不能确定一名学生的位置.在约定顺序后,(4,2)和(2,4)表示的不是同一位置.
小组讨论:表示平面上的点需要几个数据?它们有顺序吗?书写有序数对要注意什么?
反思小结:1.数轴上点的位置由一个实数确定,平面内点的位置由一对有序数对确定.2.有序数对(a,b)与(b,a)表示的意义不同,当a≠b时,它们表示两个不同的位置;当a=b时,它们表示的位置相同.
●二 有序数对的应用
活动2:
(1)现在给出班里一部分同学的姓名,约定“列数在前,排数在后”,你能快速说出这些同学座位的有序数对吗?如果约定“排数在前,列数在后”,刚才那些同学对应的有序数对会变化吗?
(2)生活中利用有序数对表示位置的情况很常见,你知道地球上的某一个地点如何确定位置吗?你能再举出生活中用有序数对表示位置的一些例子吗?
(3)通过以上几个问题的解决,加上国庆背景图案的启发,同学们能设计一些用有序数对描述的漂亮图案吗?
展示点评:约定“列前排后”与“排前列后”,同一有序数对表示的意义不一样.生活中地球上第一个地点的位置一般采用“经纬度”的方法表示.
小组讨论:有序数对中的“有序”能去掉吗?为什么?
反思小结:有序数对是指用有先后顺序两个数字来表示物体的位置,因此“有序”二字不能省略.
针对训练
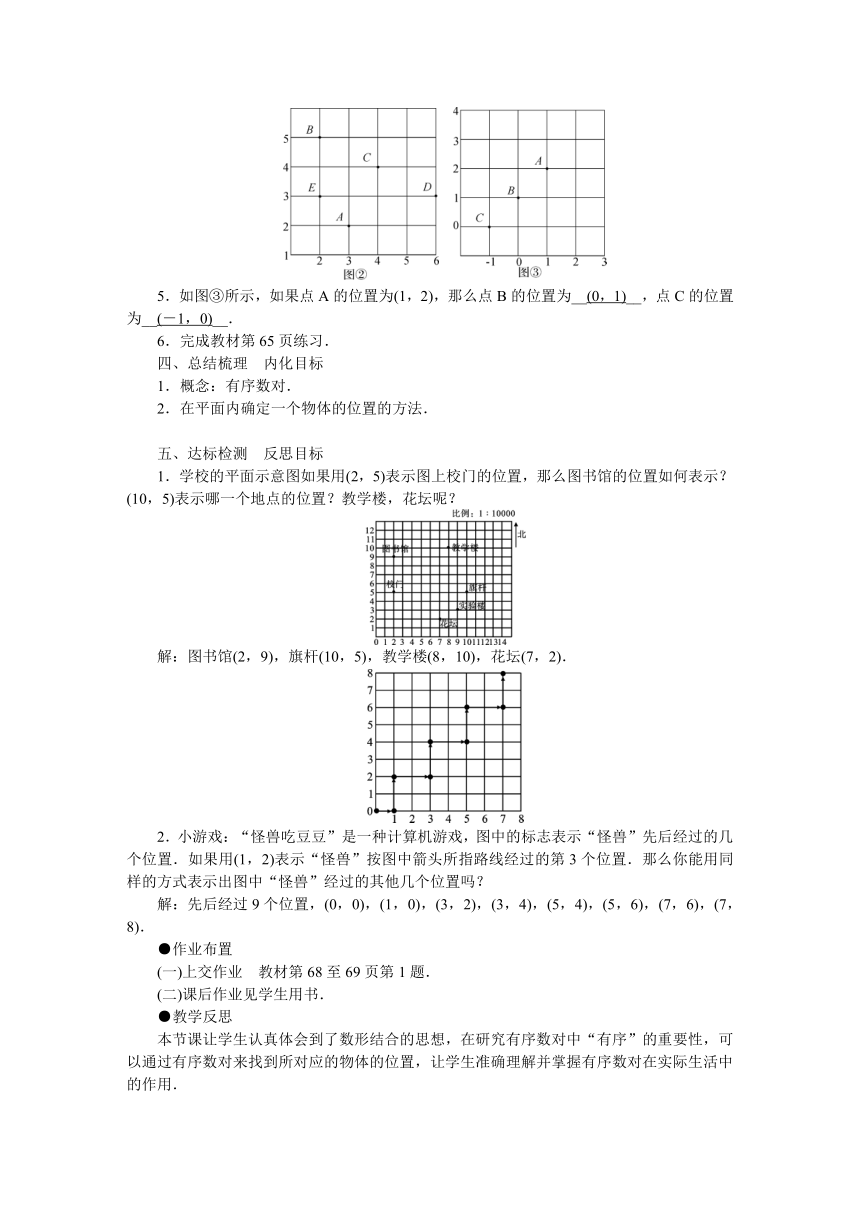
4.如图②所示,如果点A的位置为(3,2),那么点B的位置为__(2,5)__,点C的位置为__(4,4)__,点D和点E的位置分别为__(6,3),(2,3)__.
5.如图③所示,如果点A的位置为(1,2),那么点B的位置为__(0,1)__,点C的位置为__(-1,0)__.
6.完成教材第65页练习.
四、总结梳理 内化目标
1.概念:有序数对.
2.在平面内确定一个物体的位置的方法.
五、达标检测 反思目标
1.学校的平面示意图如果用(2,5)表示图上校门的位置,那么图书馆的位置如何表示?(10,5)表示哪一个地点的位置?教学楼,花坛呢?
解:图书馆(2,9),旗杆(10,5),教学楼(8,10),花坛(7,2).
2.小游戏:“怪兽吃豆豆”是一种计算机游戏,图中的标志表示“怪兽”先后经过的几个位置.如果用(1,2)表示“怪兽”按图中箭头所指路线经过的第3个位置.那么你能用同样的方式表示出图中“怪兽”经过的其他几个位置吗?
解:先后经过9个位置,(0,0),(1,0),(3,2),(3,4),(5,4),(5,6),(7,6),(7,8).
(一)上交作业 教材第68至69页第1题.
(二)课后作业见学生用书.
本节课让学生认真体会到了数形结合的思想,在研究有序数对中“有序”的重要性,可以通过有序数对来找到所对应的物体的位置,让学生准确理解并掌握有序数对在实际生活中的作用.
第2课时 平面直角坐标系
1.理解平面直角坐标系的相关概念.
2.在给定的平面直角坐标系中,能由点的位置写出点的坐标,由点的坐标确定点的位置.
平面直角坐标系及相关概念.
理解建立平面直角坐标系的必要性,理解平面直角坐标系中点与坐标的一一对应关系.
一、创设情景 明确目标
1.(1)你还记得数轴的三要素吗?
(2)请画出一条数轴,并在上面分别标出表示3和-1.5的点.
(3)分别写出数轴上点A、B、C、D表示的数.
2.在数轴上已知点能说出它的坐标,由坐标能在数轴上找到对应点的位置.那么数轴上的点与坐标有怎样的关系?
二、自主学习 指向目标
自学教材第65页至67页,请完成学生用书部分.
1.在平面内,由两条互相__垂直__、__原点__重合的数轴组成平面直角坐标系,其中水平方向的数轴叫__横__轴,也叫__x__轴,竖直方向的数轴称为__纵__轴,也叫__y__轴,两坐标轴的交点叫做__原点__.
2.在坐标平面内,两轴把坐标平面分成四部分,分别叫做__第一象限__、__第二象限__、__第三象限__、__第四象限__.坐标轴上的点不在任何一个象限内.
3.在坐标平面内,有序实数对与平面内的点__一一__对应.
三、合作探究 达成目标
●一 平面直角坐标系及相关概念
活动1:
阅读教材第65至66页,思考:
(1)类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?(例如图7.1-3中A,B,C,D各点)
(2)说一说组成平面直角坐标系的两条数轴具备什么特征?什么是横轴?什么是纵轴?什么是坐标原点?坐标平面被两条坐标轴分成了哪几个部分?分别对应什么象限?
(3)在教材第66页图7.1-4中用有序数对表示坐标图中A,B,C,D各点的坐标,说一说你是如何得到的?
展示点评:平面内两条相互垂直、原点重合的数轴,组成平面直角坐标系.
小组讨论:原点的坐标是什么?x轴和y轴上的点的坐标有什么特点?坐标轴上的点属于哪一象限?点到坐标轴的距离如何表示?
反思小结:在平面坐标系中,原点的坐标是(0,0),x轴上的点的纵坐标为0,y轴上点的横坐标为0;坐标轴上的点不属于任何象限,原点既在x轴上,又在y轴上;点到坐标轴的距离与这个点的坐标是有区别的,距离是非负数,而坐标可正可负,如点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|.
针对训练
1.将下列各点在如图所示的平面直角坐标系内描出来:(0,0),(5,-4),(3,0),(5,1),(5,-1),(3,0),(4,2),(0,0),顺次连接各点,观察所得的图形,你觉得它像什么?
解:它像一条鱼
2.完成教材第68页练习第1题.
●二 由点的坐标确定位置
活动2:
在平面直角坐标系中(图7.1-6)中找出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
展示点评:在平面直角坐标系中,由坐标确定位置,过点的横坐标与纵坐标分别作x轴,y轴的垂线,交点即为所求.
小组讨论:数轴上的点与坐标有什么关系?平面内的点与有序数对是什么关系?
反思小结:数轴上的点与实数是一一对应的,坐标平面内的点与有序数对是一一对应的.
针对训练
3.完成教材第68页练习第2题.
●三 平面直角坐标系的运用
活动3:
教材第6题图7.1-7,正方形ABCD的边长为6,如果以点A为原点,AB所在的直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A,B,C,D的坐标.
展示点评:y轴是AD所在的直线,A(0,0),B(6,0),C(6,6),D(0,6).
思考:请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是什么?比较同学之间的答案,可以得出什么结论?
小组讨论:建立适当的平面直角坐标系表示图形(物体)的位置,怎样建立平面直角坐标系较为简便地表示各顶点的坐标?
反思小结:以图形某个顶点为原点,边长为x轴或y轴建立平面直角坐标系较为简便表示其他点的坐标.
针对训练
4.(中考·菏泽)点(-2,1)在平面直角坐标系中所在的象限是( B )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(中考·湛江)在平面直角坐标系xOy中,若A点坐标为(-3,3),B点坐标为(2,0),则△ABO的面积为( D )
A.15 B.7.5 C.6 D.3
6.写出图中点A,B,C,D,E,F的坐标.观察你所写出的这些点的坐标,回答问题:
(1)在四个象限内的点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
解:A(-1,2),B(2,1),C(2,-1),D(-1,-1),E(0,3),F(-2,0).
(1)第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-).
(2)x轴上的点的纵坐标等于0,y轴上的点的横坐标等于0.
四、总结梳理 内化目标
1.概念:平面直角坐标系,横轴,纵轴,原点,坐标,象限.
2.根据点所在的位置,用“+”“-”填表:
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
3.方法:由点找出坐标,由坐标确定点的位置.
五、达标检测 反思目标
1.点(0,-3)在( B )
A.x轴上 B.y轴上
C.在原点 D.与x轴平行的直线上
2.在直角坐标系中,点A(-3,2),点B(3,2),连接AB所成的线段与__x__轴平行.
3.点P(3,4)到x轴的距离是__4__,到y轴的距离是__3__;点A到横轴的距离为8,到纵轴的距离为4,则点A的坐标为__(4,8),(4,-8),(-4,8),(-4,-8)__.
4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( B )
A.平行于x轴 B.平行于y轴 C.经过原点 D.以上都不对
5.已知长方形ABCD中,AB=5,BC=8,并且AB∥x轴,若点A的坐标为(-2,4),则点C的坐标为__(3,-4),(-7,-4)__.
6.如图,点A的坐标为(-3,4).
(1)写出图中点B、C、D、E、F、G、H的坐标,并观察点A和C,点B和D有什么关系?
(2)在图中标出(-2,4)、(5,5)、(4,-3)三点的位置.
解:(1)B(-3,-2)、C(3,-4)、D(3,2)、E(3,0)、F(-4,0)、G(0,3)、H(0,0);点A和C,点B和D,它们的横、纵坐标均互为相反数.
(一)上交作业 教材第69至70页第3,4,5题.
(二)课后作业见学生用书.
平面直角坐标系在数学学习中有非常重要的地位,它可以把几何与代数综合在一起.学生在本节课通过学习可以更进一步认识到数形结合的意义,对数学产生浓厚的兴趣.
7.1 平面直角坐标系
第1课时 有序数对
1.会用有序数对表示物体的位置.
2.结合用有序数对表示物体的位置的内容,体会数形结合的思想.
理解有序数对是怎样确定物体的位置的.
确定用怎样一对有顺序的数表示物体的位置.
一、创设情景 明确目标
在建国60周年的庆典活动中,天安门广场上出现了的背景图案,你知道它是怎么组成的吗?
二、自主学习 指向目标
自学教材第64页至65页,2.请完成学生用书部分.
1.我们把有顺序的两个数a和b组成的数对,叫做__有序数对__,记做__(a,b)__.
2.数对(a,b)和(b,a)是同一数对吗?答:__不是__.
3.在生活中常用__有序数对__、__方位角和距离__、__经纬度__等方法确定一个物体的位置.
4.下列数据不能确定物体位置的是( B )
A.5楼5号房间 B.北偏东36°
C.长征路98号 D.东经110°,北纬50°
三、合作探究 达成目标
●一 有序数对的概念
活动1:
阅读教材第64至65页,思考:
(1)同学们都有去影剧院看电影的经历,你是怎么找到自己的座位的?
(2)你若发现一本书某页有一处错误,怎样告诉其他同学这一处的位置?
(3)下图为教室的平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,5),(2,4),(4,2),(3,3),(5,6).
(4)所设在问题3中约定“列数在前,排数在后”,你能在图中标出参加数学问题讨论的同学的座位吗?
(5)怎样确定教室里座位的位置?列数和排数的先后顺序对位置有影响吗?
(6)假设我们约定“列数在前,排数在后”,请你在图中标出上述同学的位置.
(7)你所标的(2,4),(4,2)是同一个位置吗?
展示点评:在教室里,排数与列数的先后顺序没有约定的情况下,不能确定一名学生的位置.在约定顺序后,(4,2)和(2,4)表示的不是同一位置.
小组讨论:表示平面上的点需要几个数据?它们有顺序吗?书写有序数对要注意什么?
反思小结:1.数轴上点的位置由一个实数确定,平面内点的位置由一对有序数对确定.2.有序数对(a,b)与(b,a)表示的意义不同,当a≠b时,它们表示两个不同的位置;当a=b时,它们表示的位置相同.
●二 有序数对的应用
活动2:
(1)现在给出班里一部分同学的姓名,约定“列数在前,排数在后”,你能快速说出这些同学座位的有序数对吗?如果约定“排数在前,列数在后”,刚才那些同学对应的有序数对会变化吗?
(2)生活中利用有序数对表示位置的情况很常见,你知道地球上的某一个地点如何确定位置吗?你能再举出生活中用有序数对表示位置的一些例子吗?
(3)通过以上几个问题的解决,加上国庆背景图案的启发,同学们能设计一些用有序数对描述的漂亮图案吗?
展示点评:约定“列前排后”与“排前列后”,同一有序数对表示的意义不一样.生活中地球上第一个地点的位置一般采用“经纬度”的方法表示.
小组讨论:有序数对中的“有序”能去掉吗?为什么?
反思小结:有序数对是指用有先后顺序两个数字来表示物体的位置,因此“有序”二字不能省略.
针对训练
4.如图②所示,如果点A的位置为(3,2),那么点B的位置为__(2,5)__,点C的位置为__(4,4)__,点D和点E的位置分别为__(6,3),(2,3)__.
5.如图③所示,如果点A的位置为(1,2),那么点B的位置为__(0,1)__,点C的位置为__(-1,0)__.
6.完成教材第65页练习.
四、总结梳理 内化目标
1.概念:有序数对.
2.在平面内确定一个物体的位置的方法.
五、达标检测 反思目标
1.学校的平面示意图如果用(2,5)表示图上校门的位置,那么图书馆的位置如何表示?(10,5)表示哪一个地点的位置?教学楼,花坛呢?
解:图书馆(2,9),旗杆(10,5),教学楼(8,10),花坛(7,2).
2.小游戏:“怪兽吃豆豆”是一种计算机游戏,图中的标志表示“怪兽”先后经过的几个位置.如果用(1,2)表示“怪兽”按图中箭头所指路线经过的第3个位置.那么你能用同样的方式表示出图中“怪兽”经过的其他几个位置吗?
解:先后经过9个位置,(0,0),(1,0),(3,2),(3,4),(5,4),(5,6),(7,6),(7,8).
(一)上交作业 教材第68至69页第1题.
(二)课后作业见学生用书.
本节课让学生认真体会到了数形结合的思想,在研究有序数对中“有序”的重要性,可以通过有序数对来找到所对应的物体的位置,让学生准确理解并掌握有序数对在实际生活中的作用.
第2课时 平面直角坐标系
1.理解平面直角坐标系的相关概念.
2.在给定的平面直角坐标系中,能由点的位置写出点的坐标,由点的坐标确定点的位置.
平面直角坐标系及相关概念.
理解建立平面直角坐标系的必要性,理解平面直角坐标系中点与坐标的一一对应关系.
一、创设情景 明确目标
1.(1)你还记得数轴的三要素吗?
(2)请画出一条数轴,并在上面分别标出表示3和-1.5的点.
(3)分别写出数轴上点A、B、C、D表示的数.
2.在数轴上已知点能说出它的坐标,由坐标能在数轴上找到对应点的位置.那么数轴上的点与坐标有怎样的关系?
二、自主学习 指向目标
自学教材第65页至67页,请完成学生用书部分.
1.在平面内,由两条互相__垂直__、__原点__重合的数轴组成平面直角坐标系,其中水平方向的数轴叫__横__轴,也叫__x__轴,竖直方向的数轴称为__纵__轴,也叫__y__轴,两坐标轴的交点叫做__原点__.
2.在坐标平面内,两轴把坐标平面分成四部分,分别叫做__第一象限__、__第二象限__、__第三象限__、__第四象限__.坐标轴上的点不在任何一个象限内.
3.在坐标平面内,有序实数对与平面内的点__一一__对应.
三、合作探究 达成目标
●一 平面直角坐标系及相关概念
活动1:
阅读教材第65至66页,思考:
(1)类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?(例如图7.1-3中A,B,C,D各点)
(2)说一说组成平面直角坐标系的两条数轴具备什么特征?什么是横轴?什么是纵轴?什么是坐标原点?坐标平面被两条坐标轴分成了哪几个部分?分别对应什么象限?
(3)在教材第66页图7.1-4中用有序数对表示坐标图中A,B,C,D各点的坐标,说一说你是如何得到的?
展示点评:平面内两条相互垂直、原点重合的数轴,组成平面直角坐标系.
小组讨论:原点的坐标是什么?x轴和y轴上的点的坐标有什么特点?坐标轴上的点属于哪一象限?点到坐标轴的距离如何表示?
反思小结:在平面坐标系中,原点的坐标是(0,0),x轴上的点的纵坐标为0,y轴上点的横坐标为0;坐标轴上的点不属于任何象限,原点既在x轴上,又在y轴上;点到坐标轴的距离与这个点的坐标是有区别的,距离是非负数,而坐标可正可负,如点P(x,y)到x轴的距离为|y|,到y轴的距离为|x|.
针对训练
1.将下列各点在如图所示的平面直角坐标系内描出来:(0,0),(5,-4),(3,0),(5,1),(5,-1),(3,0),(4,2),(0,0),顺次连接各点,观察所得的图形,你觉得它像什么?
解:它像一条鱼
2.完成教材第68页练习第1题.
●二 由点的坐标确定位置
活动2:
在平面直角坐标系中(图7.1-6)中找出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4).
展示点评:在平面直角坐标系中,由坐标确定位置,过点的横坐标与纵坐标分别作x轴,y轴的垂线,交点即为所求.
小组讨论:数轴上的点与坐标有什么关系?平面内的点与有序数对是什么关系?
反思小结:数轴上的点与实数是一一对应的,坐标平面内的点与有序数对是一一对应的.
针对训练
3.完成教材第68页练习第2题.
●三 平面直角坐标系的运用
活动3:
教材第6题图7.1-7,正方形ABCD的边长为6,如果以点A为原点,AB所在的直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A,B,C,D的坐标.
展示点评:y轴是AD所在的直线,A(0,0),B(6,0),C(6,6),D(0,6).
思考:请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是什么?比较同学之间的答案,可以得出什么结论?
小组讨论:建立适当的平面直角坐标系表示图形(物体)的位置,怎样建立平面直角坐标系较为简便地表示各顶点的坐标?
反思小结:以图形某个顶点为原点,边长为x轴或y轴建立平面直角坐标系较为简便表示其他点的坐标.
针对训练
4.(中考·菏泽)点(-2,1)在平面直角坐标系中所在的象限是( B )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(中考·湛江)在平面直角坐标系xOy中,若A点坐标为(-3,3),B点坐标为(2,0),则△ABO的面积为( D )
A.15 B.7.5 C.6 D.3
6.写出图中点A,B,C,D,E,F的坐标.观察你所写出的这些点的坐标,回答问题:
(1)在四个象限内的点的坐标各有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
解:A(-1,2),B(2,1),C(2,-1),D(-1,-1),E(0,3),F(-2,0).
(1)第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-).
(2)x轴上的点的纵坐标等于0,y轴上的点的横坐标等于0.
四、总结梳理 内化目标
1.概念:平面直角坐标系,横轴,纵轴,原点,坐标,象限.
2.根据点所在的位置,用“+”“-”填表:
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
3.方法:由点找出坐标,由坐标确定点的位置.
五、达标检测 反思目标
1.点(0,-3)在( B )
A.x轴上 B.y轴上
C.在原点 D.与x轴平行的直线上
2.在直角坐标系中,点A(-3,2),点B(3,2),连接AB所成的线段与__x__轴平行.
3.点P(3,4)到x轴的距离是__4__,到y轴的距离是__3__;点A到横轴的距离为8,到纵轴的距离为4,则点A的坐标为__(4,8),(4,-8),(-4,8),(-4,-8)__.
4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( B )
A.平行于x轴 B.平行于y轴 C.经过原点 D.以上都不对
5.已知长方形ABCD中,AB=5,BC=8,并且AB∥x轴,若点A的坐标为(-2,4),则点C的坐标为__(3,-4),(-7,-4)__.
6.如图,点A的坐标为(-3,4).
(1)写出图中点B、C、D、E、F、G、H的坐标,并观察点A和C,点B和D有什么关系?
(2)在图中标出(-2,4)、(5,5)、(4,-3)三点的位置.
解:(1)B(-3,-2)、C(3,-4)、D(3,2)、E(3,0)、F(-4,0)、G(0,3)、H(0,0);点A和C,点B和D,它们的横、纵坐标均互为相反数.
(一)上交作业 教材第69至70页第3,4,5题.
(二)课后作业见学生用书.
平面直角坐标系在数学学习中有非常重要的地位,它可以把几何与代数综合在一起.学生在本节课通过学习可以更进一步认识到数形结合的意义,对数学产生浓厚的兴趣.
