人教版七年级数学下册5.3平行线的性质 教案(2课时)
文档属性
| 名称 | 人教版七年级数学下册5.3平行线的性质 教案(2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 104.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 23:27:54 | ||
图片预览


文档简介
5.3 平行线的性质
第1课时 平行线的性质
1.探索并掌握平行线的性质;
2.能够综合运用平行线的性质与判定进行推理.
掌握平行线的三条性质.
理解平行线的性质和判定的区别和联系.
一、创设情景 明确目标
根据同位角相等,或内错角相等,或者同旁内角互补,可以判定两直线平行.反过来,如果两直线平行,同位角之间有什么关系?内错角,同旁内角之间又有什么关系呢?
二、自主学习 指向目标
自学教材第18至19页,请完成学生用书部分.
1.两直线平行,同位角__相等__.
2.两直线平行,内错角__相等__.
3.两直线平行,同旁内角__互补__.
三、合作探究 达成目标
●一 平行线的性质
活动1:
仔细阅读教材第18页内容,通过度量、填表比较后思考:
(1)两直线平行时,同位角之间的关系如何?
(2)你是通过什么方法得到上述结论的?
(3)平行线的这一性质怎样用几何符号语言表示?
(4)如图,已知:a∥b,那么∠3与∠5有什么关系?
因为a∥b,所以∠1=∠5( )
又因为∠1=________(对顶角相等),所以∠5=∠3.
结论:平行线的性质2:________________________________________________________________________.
(5)已知a∥b,那么∠4与∠5有什么关系呢?
结论:平行线的性质3:________________________________________________________________________.
展示点评:两条平行线被第三条直线所截,同位角相等、内错角相等、同旁内角互补.
小组讨论:平行线的性质与它的判定之间有什么关系?
反思小结:平行线的判定是已知角的关系得到直线的平行,而平行线的性质是已知直线的平行得到角的关系.
针对训练
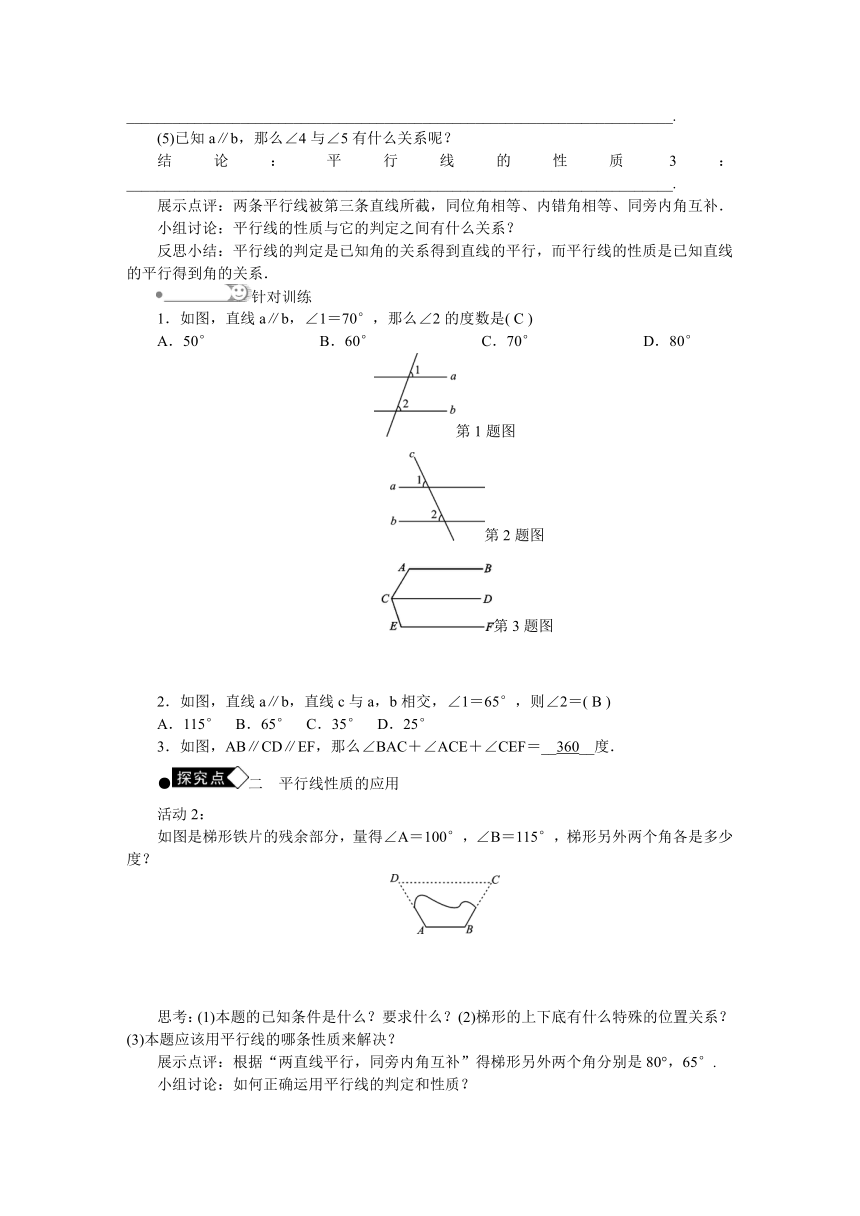
1.如图,直线a∥b,∠1=70°,那么∠2的度数是( C )
A.50° B.60° C.70° D.80°
第1题图
第2题图
第3题图
2.如图,直线a∥b,直线c与a,b相交,∠1=65°,则∠2=( B )
A.115° B.65° C.35° D.25°
3.如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=__360__度.
●二 平行线性质的应用
活动2:
如图是梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角各是多少度?
思考:(1)本题的已知条件是什么?要求什么?(2)梯形的上下底有什么特殊的位置关系?(3)本题应该用平行线的哪条性质来解决?
展示点评:根据“两直线平行,同旁内角互补”得梯形另外两个角分别是80°,65°.
小组讨论:如何正确运用平行线的判定和性质?
反思小结:平行线的性质与判定正好相反,应用时必须辨别清楚,判断两直线平行时用判定,已知直线平行时用性质.
针对训练
4.如图,AB∥CD,∠ACE=∠ECD,∠A=118°,则∠AEC等于( B )
A.62° B.31° C.59° D.29.5°
5.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,交CD于G,∠1=40°,求∠2的度数.
解:因为AB∥CD,所以∠1+∠BEF=180°,
所以∠BEF=140°,
又EG平分∠BEF,
所以∠BEG=∠BEF=70°,
因为AB∥CD,
所以∠2=∠BEG=70°
四、总结梳理 内化目标
回顾本节课学习内容,请回答下列问题:
1.本节课你学习了平行线的哪几条性质?
2.平行线的判定和性质有什么区别和联系?应用时要注意什么?
五、达标检测 反思目标
1.如图,(1)若AD∥BC,则∠__1__=∠__5__,∠__8__=∠__4__,∠ABC+∠__BAD__=180°;
(2)若DC∥AB,则∠__3__=∠__7__,∠__2__=∠__6__,∠ABC+∠__BCD__=180°.
2.如图:AB∥CD,∠A=98°,∠C=75°,则∠B=__105°__,∠D=__82°__.
第1题图
第2题图
第3题图
3.如图:AB∥CD,∠A=80°,∠B=60°,则∠ACB=__40__度.
4.已知:如图,AD∥BC,∠AEF=∠B.
求证:AD∥EF.
证明:∵AD∥BC,(已知)
∴∠A+∠B=180°.
(__两直线平行,同旁内角互补__)
∵∠AEF=∠B,(已知)
∴∠A+∠__AEF__=180°,(等量代换)
∴AD∥EF.
(__同旁内角互补,两直线平行__)
(一)上交作业 教材第22至23页第2、3、4、6题.
(二)课后作业见学生用书.
平行线的性质是在平行线的判定的基础上产生的,它们之间有完美的对称性,让学生能深刻地体会到这一点,能够正确地区分平行线的判定与性质,在不同题目中灵活应用平行线的性质与判定.
第2课时 命题、定理、证明
1.了解命题的结构和概念;
2.会判断一个命题的真假;
3.了解什么是定理和证明.
会判断一个命题的真假,了解定理的概念.
能够分清命题的题设和结论,会把命题写成“如果…,那么…”的形式.
一、创设情景 明确目标
歌德是18世纪德国的一位著名文艺大师,一天,他与一位批评家“狭路相逢”,这位文艺批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,边走边大声说道:“我从来不给傻子让路!”而对如此的尴尬的局面,歌德笑容可掬,谦恭的闪在一旁,有礼貌地回答道“呵呵,我可恰相反”,结果故作聪明的批评家,反倒自讨没趣.你知道为什么吗?
二、自主学习 指向目标
自学教材第20至22页,请完成学生用书部分.
1.判断一件事情的语句,叫做__命题__,命题由__题设__和__结论__两部分组成.
2.任何一个命题都可以写成__如果……那么……__的形式,正确的命题叫__真命题__,错误的命题叫__假命题__.
3.一个命题是真命题,它的正确性是经过推理证实的,这样的真命题叫做__定理__.
4.命题“对顶角相等”的题设是__两个角是对顶角__.
5.“同位角相等”是__假__命题.(填“真”或“假”).
三、合作探究 达成目标
●一 命题、定理
活动1:
仔细阅读教材第20页至第21页,思考下列问题:
(1)什么叫命题?
(2)命题可以分成哪两部分?怎样将命题改写成“如果……那么……”的形式?
(3)什么叫真命题?什么叫假命题?请举例说明.
(4)什么叫定理?怎样判断一个命题的真假?请举例说明.
展示点评:判断一件事情的语句叫命题.任何一个命题都是由题设和结论两部分组成.
小组讨论:把一个命题改写成“如果……那么……”的形式,应注意什么问题?
反思小结:一个命题的题设就是“如果”引出的部分,结论就是“那么”引出的部分.对那些题设和结论不明显的命题先把它改成“如果”“那么”的形式后再写.真命题强调“一定成立”无一例外,假命题强调“不能保证结论一定成立”,所以要说明一个命题是假命题只要能举出一个反例即可.
针对训练
1.下列语句属于命题的是( A )
A.若|a|=|b|,则a=b. B.延长线段AB至C.
C.今天会下雨吗? D.向雷锋同志学习.
2.下列命题中,为真命题的是( C )
A.相等的两个角是对顶角 B.点到直线的距离是这点到这条直线所作的垂线段
C.等角的补角相等 D.两条直线被第三条直线所截,内错角相等
3.把命题“两直线相交,只有一个交点”改写成“如果……那么……”的形式为__如果两直线相交,那么它们只有一个交点__.
4.见教材21页课后练习.
●二 证明
活动2:
如图,已知直线b∥c,a⊥b,求证:a⊥c.
思考:要证“a⊥c”,需要证明哪个角为90°?由题目中的已知条件能够得出什么结论?
展示点评:证明中的每一步推理都要有根据,不能“想当然”,这些根据可以是已知条件,也可以是已经学过的定义、基本事实、定理等.
小组讨论:如何判断一个命题是假命题?在证明时,注意什么问题?
针对训练
5.如图所示,已知C,P,D三点在同一条直线上,∠BAP与∠APD互补,∠1=∠2.求证:∠E=∠F.
证明:∵∠BAP+∠APD=180°(__已知__),
∴AB∥CD(__同旁内角互补,两直线平行__),
∴∠BAP=∠APC(__两直线平行,内错角相等__),
又∵∠1=∠2(__已知__),
∴∠BAP-∠2=∠APC-∠1(__等式的性质__),
即∠EAP=∠APF,
∴AE∥PF(__内错角相等,两直线平行__),
∴∠E=∠F(__两直线平行,内错角相等__).
★反思小结:
1.命题含有“判定”“断定”的意思,这是判断一个语句是否为命题的依据,问句和对作图过程的描述都不是命题.
2.命题的题设和结论分不清时,先把它改写成“如果……那么……”的形式.
3.真命题需要推理论证,而假命题只需举一个反例来说明它是错误的.
4.证明中的每一步推理都要有根据,不能“想当然”.这些根据可以是已知条件,也可以是已经学过的定义、基本事实、定理等.
四、总结梳理 内化目标
回顾本节课学习内容,请回答下列问题:
1.怎样判别一个句子是命题?
2.请举例说出一个命题的条件部分和结论部分.
3.怎样判断一个命题是“真命题”或是“假命题”?
五、达标检测 反思目标
1.下列句子哪些是命题:
(1)猴子是动物的一种
(2)你的作业呢?
(3)美丽的天空
(4)所有的质数都是奇数
(5)负数都小于零
(6)过直线外一点作直线l的平行线.
解:(1)(4)(5)是命题,其它不是.
2.指出下列命题的题设和结论
(1)对顶角相等;
(2)相等的角是对顶角;
(3)互补的角是邻补角;
(4)等角的补角相等;
(5)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线就平行;
(6)两直线平行,内错角相等.
3.判断下列命题是真命题,还是假命题,若是假命题,举出一个反例.
(1)邻补角是互补的角;
(2)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线就平行;
(3)两条直线被第三条直线所截,同旁内角互补.
解:(2)是真命题,(1)(3)是假命题.
4.如图,AB∥CD,CE平分∠BCD
求证:∠DCE=∠B
证明:∵AB∥CD∴∠B=∠BCD ∵CE平分∠BCD∴∠DCE=∠BCD
∴∠DCE=∠B
(一)上交作业 教材24—25页第12、13题.
(二)课后作业见学生用书.
本节课主要学习“命题、定理、证明”三个概念,让学生理解到一个命题由题设和结论构成,若一个命题题设和结论都正确,它就是一个真命题,否则就是假命题,因此所有的定理都是真命题,而且又进一步认识到定理必须经过某些依据总结归纳,形成一个逻辑推理过程,这样的一个过程就叫做证明.
第1课时 平行线的性质
1.探索并掌握平行线的性质;
2.能够综合运用平行线的性质与判定进行推理.
掌握平行线的三条性质.
理解平行线的性质和判定的区别和联系.
一、创设情景 明确目标
根据同位角相等,或内错角相等,或者同旁内角互补,可以判定两直线平行.反过来,如果两直线平行,同位角之间有什么关系?内错角,同旁内角之间又有什么关系呢?
二、自主学习 指向目标
自学教材第18至19页,请完成学生用书部分.
1.两直线平行,同位角__相等__.
2.两直线平行,内错角__相等__.
3.两直线平行,同旁内角__互补__.
三、合作探究 达成目标
●一 平行线的性质
活动1:
仔细阅读教材第18页内容,通过度量、填表比较后思考:
(1)两直线平行时,同位角之间的关系如何?
(2)你是通过什么方法得到上述结论的?
(3)平行线的这一性质怎样用几何符号语言表示?
(4)如图,已知:a∥b,那么∠3与∠5有什么关系?
因为a∥b,所以∠1=∠5( )
又因为∠1=________(对顶角相等),所以∠5=∠3.
结论:平行线的性质2:________________________________________________________________________.
(5)已知a∥b,那么∠4与∠5有什么关系呢?
结论:平行线的性质3:________________________________________________________________________.
展示点评:两条平行线被第三条直线所截,同位角相等、内错角相等、同旁内角互补.
小组讨论:平行线的性质与它的判定之间有什么关系?
反思小结:平行线的判定是已知角的关系得到直线的平行,而平行线的性质是已知直线的平行得到角的关系.
针对训练
1.如图,直线a∥b,∠1=70°,那么∠2的度数是( C )
A.50° B.60° C.70° D.80°
第1题图
第2题图
第3题图
2.如图,直线a∥b,直线c与a,b相交,∠1=65°,则∠2=( B )
A.115° B.65° C.35° D.25°
3.如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=__360__度.
●二 平行线性质的应用
活动2:
如图是梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角各是多少度?
思考:(1)本题的已知条件是什么?要求什么?(2)梯形的上下底有什么特殊的位置关系?(3)本题应该用平行线的哪条性质来解决?
展示点评:根据“两直线平行,同旁内角互补”得梯形另外两个角分别是80°,65°.
小组讨论:如何正确运用平行线的判定和性质?
反思小结:平行线的性质与判定正好相反,应用时必须辨别清楚,判断两直线平行时用判定,已知直线平行时用性质.
针对训练
4.如图,AB∥CD,∠ACE=∠ECD,∠A=118°,则∠AEC等于( B )
A.62° B.31° C.59° D.29.5°
5.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,交CD于G,∠1=40°,求∠2的度数.
解:因为AB∥CD,所以∠1+∠BEF=180°,
所以∠BEF=140°,
又EG平分∠BEF,
所以∠BEG=∠BEF=70°,
因为AB∥CD,
所以∠2=∠BEG=70°
四、总结梳理 内化目标
回顾本节课学习内容,请回答下列问题:
1.本节课你学习了平行线的哪几条性质?
2.平行线的判定和性质有什么区别和联系?应用时要注意什么?
五、达标检测 反思目标
1.如图,(1)若AD∥BC,则∠__1__=∠__5__,∠__8__=∠__4__,∠ABC+∠__BAD__=180°;
(2)若DC∥AB,则∠__3__=∠__7__,∠__2__=∠__6__,∠ABC+∠__BCD__=180°.
2.如图:AB∥CD,∠A=98°,∠C=75°,则∠B=__105°__,∠D=__82°__.
第1题图
第2题图
第3题图
3.如图:AB∥CD,∠A=80°,∠B=60°,则∠ACB=__40__度.
4.已知:如图,AD∥BC,∠AEF=∠B.
求证:AD∥EF.
证明:∵AD∥BC,(已知)
∴∠A+∠B=180°.
(__两直线平行,同旁内角互补__)
∵∠AEF=∠B,(已知)
∴∠A+∠__AEF__=180°,(等量代换)
∴AD∥EF.
(__同旁内角互补,两直线平行__)
(一)上交作业 教材第22至23页第2、3、4、6题.
(二)课后作业见学生用书.
平行线的性质是在平行线的判定的基础上产生的,它们之间有完美的对称性,让学生能深刻地体会到这一点,能够正确地区分平行线的判定与性质,在不同题目中灵活应用平行线的性质与判定.
第2课时 命题、定理、证明
1.了解命题的结构和概念;
2.会判断一个命题的真假;
3.了解什么是定理和证明.
会判断一个命题的真假,了解定理的概念.
能够分清命题的题设和结论,会把命题写成“如果…,那么…”的形式.
一、创设情景 明确目标
歌德是18世纪德国的一位著名文艺大师,一天,他与一位批评家“狭路相逢”,这位文艺批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,边走边大声说道:“我从来不给傻子让路!”而对如此的尴尬的局面,歌德笑容可掬,谦恭的闪在一旁,有礼貌地回答道“呵呵,我可恰相反”,结果故作聪明的批评家,反倒自讨没趣.你知道为什么吗?
二、自主学习 指向目标
自学教材第20至22页,请完成学生用书部分.
1.判断一件事情的语句,叫做__命题__,命题由__题设__和__结论__两部分组成.
2.任何一个命题都可以写成__如果……那么……__的形式,正确的命题叫__真命题__,错误的命题叫__假命题__.
3.一个命题是真命题,它的正确性是经过推理证实的,这样的真命题叫做__定理__.
4.命题“对顶角相等”的题设是__两个角是对顶角__.
5.“同位角相等”是__假__命题.(填“真”或“假”).
三、合作探究 达成目标
●一 命题、定理
活动1:
仔细阅读教材第20页至第21页,思考下列问题:
(1)什么叫命题?
(2)命题可以分成哪两部分?怎样将命题改写成“如果……那么……”的形式?
(3)什么叫真命题?什么叫假命题?请举例说明.
(4)什么叫定理?怎样判断一个命题的真假?请举例说明.
展示点评:判断一件事情的语句叫命题.任何一个命题都是由题设和结论两部分组成.
小组讨论:把一个命题改写成“如果……那么……”的形式,应注意什么问题?
反思小结:一个命题的题设就是“如果”引出的部分,结论就是“那么”引出的部分.对那些题设和结论不明显的命题先把它改成“如果”“那么”的形式后再写.真命题强调“一定成立”无一例外,假命题强调“不能保证结论一定成立”,所以要说明一个命题是假命题只要能举出一个反例即可.
针对训练
1.下列语句属于命题的是( A )
A.若|a|=|b|,则a=b. B.延长线段AB至C.
C.今天会下雨吗? D.向雷锋同志学习.
2.下列命题中,为真命题的是( C )
A.相等的两个角是对顶角 B.点到直线的距离是这点到这条直线所作的垂线段
C.等角的补角相等 D.两条直线被第三条直线所截,内错角相等
3.把命题“两直线相交,只有一个交点”改写成“如果……那么……”的形式为__如果两直线相交,那么它们只有一个交点__.
4.见教材21页课后练习.
●二 证明
活动2:
如图,已知直线b∥c,a⊥b,求证:a⊥c.
思考:要证“a⊥c”,需要证明哪个角为90°?由题目中的已知条件能够得出什么结论?
展示点评:证明中的每一步推理都要有根据,不能“想当然”,这些根据可以是已知条件,也可以是已经学过的定义、基本事实、定理等.
小组讨论:如何判断一个命题是假命题?在证明时,注意什么问题?
针对训练
5.如图所示,已知C,P,D三点在同一条直线上,∠BAP与∠APD互补,∠1=∠2.求证:∠E=∠F.
证明:∵∠BAP+∠APD=180°(__已知__),
∴AB∥CD(__同旁内角互补,两直线平行__),
∴∠BAP=∠APC(__两直线平行,内错角相等__),
又∵∠1=∠2(__已知__),
∴∠BAP-∠2=∠APC-∠1(__等式的性质__),
即∠EAP=∠APF,
∴AE∥PF(__内错角相等,两直线平行__),
∴∠E=∠F(__两直线平行,内错角相等__).
★反思小结:
1.命题含有“判定”“断定”的意思,这是判断一个语句是否为命题的依据,问句和对作图过程的描述都不是命题.
2.命题的题设和结论分不清时,先把它改写成“如果……那么……”的形式.
3.真命题需要推理论证,而假命题只需举一个反例来说明它是错误的.
4.证明中的每一步推理都要有根据,不能“想当然”.这些根据可以是已知条件,也可以是已经学过的定义、基本事实、定理等.
四、总结梳理 内化目标
回顾本节课学习内容,请回答下列问题:
1.怎样判别一个句子是命题?
2.请举例说出一个命题的条件部分和结论部分.
3.怎样判断一个命题是“真命题”或是“假命题”?
五、达标检测 反思目标
1.下列句子哪些是命题:
(1)猴子是动物的一种
(2)你的作业呢?
(3)美丽的天空
(4)所有的质数都是奇数
(5)负数都小于零
(6)过直线外一点作直线l的平行线.
解:(1)(4)(5)是命题,其它不是.
2.指出下列命题的题设和结论
(1)对顶角相等;
(2)相等的角是对顶角;
(3)互补的角是邻补角;
(4)等角的补角相等;
(5)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线就平行;
(6)两直线平行,内错角相等.
3.判断下列命题是真命题,还是假命题,若是假命题,举出一个反例.
(1)邻补角是互补的角;
(2)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线就平行;
(3)两条直线被第三条直线所截,同旁内角互补.
解:(2)是真命题,(1)(3)是假命题.
4.如图,AB∥CD,CE平分∠BCD
求证:∠DCE=∠B
证明:∵AB∥CD∴∠B=∠BCD ∵CE平分∠BCD∴∠DCE=∠BCD
∴∠DCE=∠B
(一)上交作业 教材24—25页第12、13题.
(二)课后作业见学生用书.
本节课主要学习“命题、定理、证明”三个概念,让学生理解到一个命题由题设和结论构成,若一个命题题设和结论都正确,它就是一个真命题,否则就是假命题,因此所有的定理都是真命题,而且又进一步认识到定理必须经过某些依据总结归纳,形成一个逻辑推理过程,这样的一个过程就叫做证明.
