23.3 事件的概率 课件(21张PPT)
文档属性
| 名称 | 23.3 事件的概率 课件(21张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
红烧肉
宫保鸡丁
糖醋排骨
可乐鸡翅
按 钮
菜单转盘
事件的概率
问题
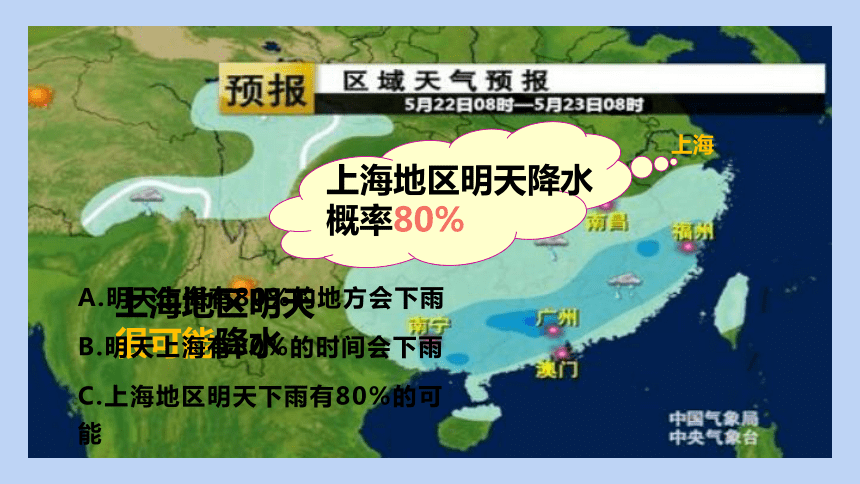
上海
上海地区明天降水概率80%
上海地区明天很可能降水
A.明天上海有80%的地方会下雨
B.明天上海有80%的时间会下雨
C.上海地区明天下雨有80%的可能
概率:
表示某事件发生的可能性大小的数。
为了叙述方便,我们用大写的英文字母表示事件,如事件A、B……等;
事件A的概率,记作P(A)
概念
事件概率的线段图
0
不可能事件的概率
很可能发生事件的概率
1
必然事件的概率
随机事件的概率
很不可能发生
事件的概率
写出下列事件的概率(填“接近1”,“接近0”,“=1”或“=0”)
01
用A表示“上海天天是晴天”,则P(A)_____
02
用B表示“新买的圆珠笔写得出字”,则P(B)________
03
用C表示“坐火车出行,遭遇出轨”,则P(C)_____
04
用D表示“当m是正整数时,2m是偶数”,则P(D)________
=0
接近1
接近0
=1
问题探究
抛掷一枚均匀的硬币,
“恰好正面朝上”的概率是多少?
01
每位成员完成5次抛掷硬币模拟实验,统计硬币正面朝上次数,计算出“正面朝上次数与实验总次数5比值”
02
每组记录员记录、统计和汇总整个小组正面朝上出现的次数与实验总次数
03
小组内计算出20次实验的“正面朝上次数与实验总次数比值”
04
每组把实验数据写到黑板表格中
实验一步骤
实验完成时间:8分钟
实验探究
HTML模拟硬币实验小程序
01
明确每位成员的职责(记录员、输入员、报数员和监督员)
02
以小组为单位,从100~10000000任取5个数据,从小到大依次填写到表格中
03
进行大数实验,记录好实验实验数据
04
观察表格、柱状图和折线统计图
组内交流,得出结论,写在纸张上,班上汇报
实验二步骤
实验完成时间:8分钟
实验结论
抛掷一枚均匀的硬币,
“恰好正面朝上”的概率是0.5
统计学家投硬币实验
试验者 试验次数n 正面出现的次数k 出现正面的频率n/k
布丰 4040 2048 0.5069
德·摩根 4092 2048 0.5005
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
总结探究
一般地,在大量重复进行同一试验后得到的频率,总是接近于某个常数,通常把这个常数作为这个事件概率的估计值
频率与概率有什么区别与联系?
TEST
达标检测
课堂小结
1. 概率是表示事件可能性大小的数
2. 必然事件U的概率为1, 记作P(U)=1
不可能事件V的概率为0,记作 P(V)=0
随机事件A的概率范围为:0课堂小结
3. 频率与概率的区别与联系
(1)频率是变化值,概率是固定值
(2)当进行大量实验时,频率无限接近于概率
4. 概率与生活息息相关
5. 计算机的便捷性
TASK
小组提高任务
任务一(坐庄法)
某篮球运动员在同一条件下进行投篮练习,结果如下表:
投篮次数 8 10 15 20 30 40 50
进球次数 6 8 12 17 25 32 39
进球频率
计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少
这位运动员进球的概率是0.8,那么他投10次篮一定能投中8次吗
0.78
0.75
0.80
0.80
0.85
0.83
0.80
概率约是0.8
不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的.
任务二
全班同学一起做摸球试验,布袋里的球除了有红白两种颜色外其他都一样。每次从布袋里摸出一个球,记下颜色后放回摇匀。一共摸了200次,其中131次摸出白球。如果布袋里有3个球,请你估计布袋里红球和白球的个数。
1红2白
作业布置
A
2.查阅概率发展史
1.练习册23.3 1-3
B
1.练习册23.3 1-2
2.P128 2
3.查阅概率发展史
感谢大家的聆听
—THANK YOU—
红烧肉
宫保鸡丁
糖醋排骨
可乐鸡翅
按 钮
菜单转盘
事件的概率
问题
上海
上海地区明天降水概率80%
上海地区明天很可能降水
A.明天上海有80%的地方会下雨
B.明天上海有80%的时间会下雨
C.上海地区明天下雨有80%的可能
概率:
表示某事件发生的可能性大小的数。
为了叙述方便,我们用大写的英文字母表示事件,如事件A、B……等;
事件A的概率,记作P(A)
概念
事件概率的线段图
0
不可能事件的概率
很可能发生事件的概率
1
必然事件的概率
随机事件的概率
很不可能发生
事件的概率
写出下列事件的概率(填“接近1”,“接近0”,“=1”或“=0”)
01
用A表示“上海天天是晴天”,则P(A)_____
02
用B表示“新买的圆珠笔写得出字”,则P(B)________
03
用C表示“坐火车出行,遭遇出轨”,则P(C)_____
04
用D表示“当m是正整数时,2m是偶数”,则P(D)________
=0
接近1
接近0
=1
问题探究
抛掷一枚均匀的硬币,
“恰好正面朝上”的概率是多少?
01
每位成员完成5次抛掷硬币模拟实验,统计硬币正面朝上次数,计算出“正面朝上次数与实验总次数5比值”
02
每组记录员记录、统计和汇总整个小组正面朝上出现的次数与实验总次数
03
小组内计算出20次实验的“正面朝上次数与实验总次数比值”
04
每组把实验数据写到黑板表格中
实验一步骤
实验完成时间:8分钟
实验探究
HTML模拟硬币实验小程序
01
明确每位成员的职责(记录员、输入员、报数员和监督员)
02
以小组为单位,从100~10000000任取5个数据,从小到大依次填写到表格中
03
进行大数实验,记录好实验实验数据
04
观察表格、柱状图和折线统计图
组内交流,得出结论,写在纸张上,班上汇报
实验二步骤
实验完成时间:8分钟
实验结论
抛掷一枚均匀的硬币,
“恰好正面朝上”的概率是0.5
统计学家投硬币实验
试验者 试验次数n 正面出现的次数k 出现正面的频率n/k
布丰 4040 2048 0.5069
德·摩根 4092 2048 0.5005
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
总结探究
一般地,在大量重复进行同一试验后得到的频率,总是接近于某个常数,通常把这个常数作为这个事件概率的估计值
频率与概率有什么区别与联系?
TEST
达标检测
课堂小结
1. 概率是表示事件可能性大小的数
2. 必然事件U的概率为1, 记作P(U)=1
不可能事件V的概率为0,记作 P(V)=0
随机事件A的概率范围为:0
3. 频率与概率的区别与联系
(1)频率是变化值,概率是固定值
(2)当进行大量实验时,频率无限接近于概率
4. 概率与生活息息相关
5. 计算机的便捷性
TASK
小组提高任务
任务一(坐庄法)
某篮球运动员在同一条件下进行投篮练习,结果如下表:
投篮次数 8 10 15 20 30 40 50
进球次数 6 8 12 17 25 32 39
进球频率
计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少
这位运动员进球的概率是0.8,那么他投10次篮一定能投中8次吗
0.78
0.75
0.80
0.80
0.85
0.83
0.80
概率约是0.8
不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的.
任务二
全班同学一起做摸球试验,布袋里的球除了有红白两种颜色外其他都一样。每次从布袋里摸出一个球,记下颜色后放回摇匀。一共摸了200次,其中131次摸出白球。如果布袋里有3个球,请你估计布袋里红球和白球的个数。
1红2白
作业布置
A
2.查阅概率发展史
1.练习册23.3 1-3
B
1.练习册23.3 1-2
2.P128 2
3.查阅概率发展史
感谢大家的聆听
—THANK YOU—
