22.5(1) 等腰梯形性质 课件(28张PPT)
文档属性
| 名称 | 22.5(1) 等腰梯形性质 课件(28张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览





文档简介
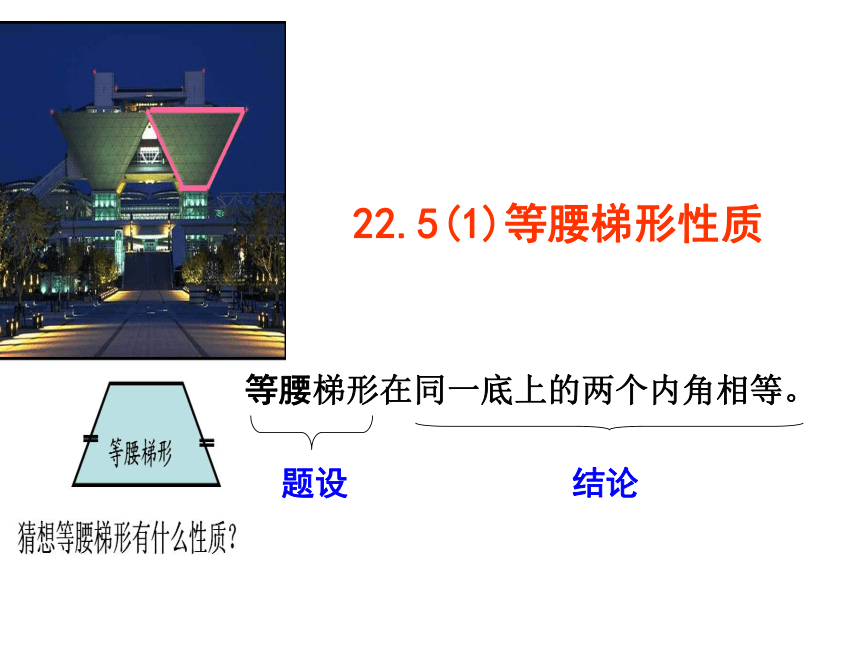
课件28张PPT。充分利用3个等腰三角形以及等腰梯形定义操作:
长方形和等腰三角形都平放交叠在一起,重叠部分是什么形,为什么?要养成猜想后推理证明的习惯。你找到等腰梯形了吗?你找到等腰梯形了吗?你找到等腰梯形了吗?猜想等腰梯形有什么性质?
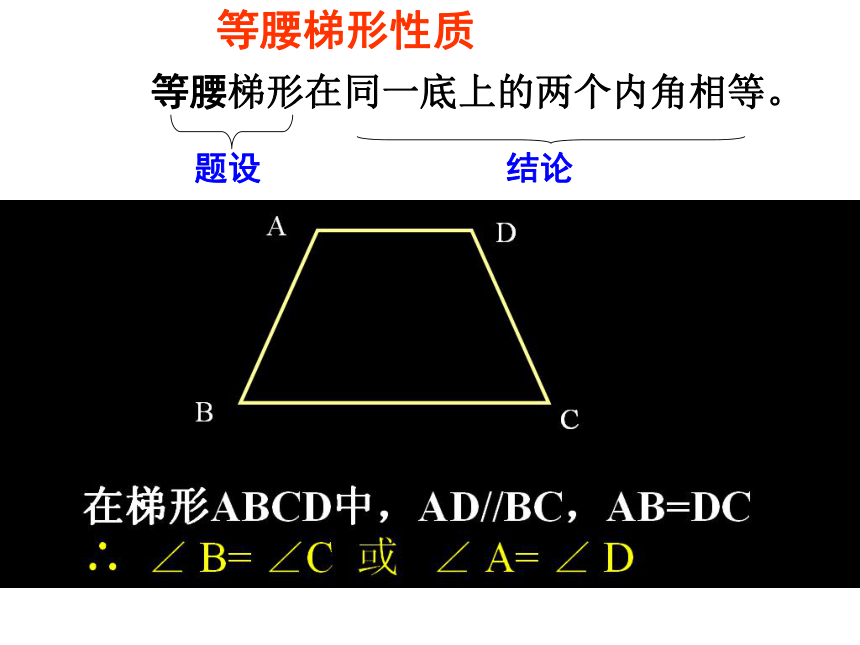
提示:从角考虑。 题设等腰梯形在同一底上的两个内角相等。结论22.5(1)等腰梯形性质 题设等腰梯形在同一底上的两个内角相等。结论等腰梯形性质 等腰梯形的性质已知:梯形ABCD中,AD // BC,AB = DC
求证: ∠B = ∠C
证明:过点D作DE // AB交BC于E
∵ AD // BC,∴ AB = DE
∵ AB = DC ,∴ DE = DC
∴∠1 =∠C
∵ DE // AB
∴ ∠1 = ∠B
∴ ∠B = ∠C
∠A = ∠CDA还要从新证起吗?
等腰梯形的性质证明:过点A,D分别作AE ⊥BC于E
DF ⊥BC于 F
∵ AE//DF,AD//BC
∴ AE=DF
∵ AB=DC
∴ Rt △ABE≌Rt △ DCF (H.L)
∴ ∠ B= ∠ C
已知:梯形ABCD中,AD//BC,AB=DC
求证: ∠B= ∠C
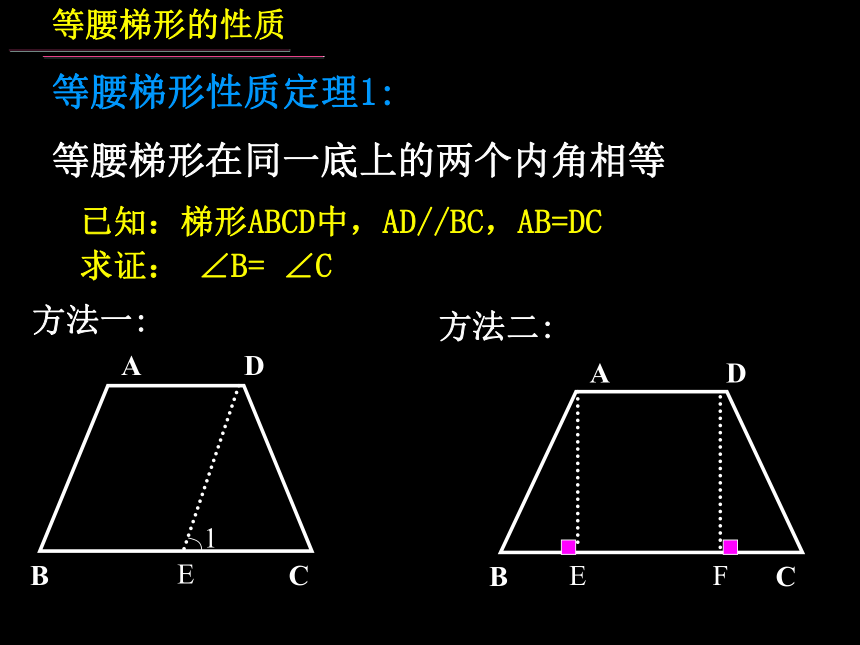
求证:等腰梯形在同一底上的两个内角相等等腰梯形的性质等腰梯形性质定理1:
等腰梯形在同一底上的两个内角相等已知:梯形ABCD中,AD//BC,AB=DC
求证: ∠B= ∠C
方法一:
方法二:等腰梯形的性质 等腰梯形性质定理1: 等腰梯形在同一底上的两个内角相等已知:梯形ABCD中,AD//BC,AB=DC
求证: ∠B= ∠C
方法三:
E请回家完成方法三
若还有新方法也请自行完成现已知等腰梯形,
求证上方是等腰三角形。操作:
长方形和等腰三角形都平放交叠在一起,重叠部分是什么形,为什么??例题1:已知:梯形ABCD中,AD//BC,腰BA和CD的延长线交于点E.
求证: △EAD是等腰三角形.证明 ∵四边形ABCD是等腰梯形, AD//BC ,
∴ ∠B= ∠C (等腰梯形在同一底上的两个内角相等)
∵ AD//BC
∴ ∠1= ∠B ,∠2= ∠C ,
∴ ∠1= ∠2
∴ △EAD是等腰三角形.
12新问题老问题等腰梯形三角形或特殊四边形转化转化学 有 所 获等腰梯形性质巩固练习1:如图,在等腰梯形ABCD中,
AD∥BC ,AD=AB,BD⊥DC,
求∠C的度数。 题设结论等腰梯形性质 等腰梯形的除了“等腰梯形在同一底上的两个内角相等”还有什么性质?提示:从对角线考虑。 题设结论等腰梯形性质 等腰梯形的两条对角线相等。等腰梯形的两条对角线相等。题设结论等腰梯形性质: ∴ AC=BD等腰梯形的性质定理:性质定理1 等腰梯形在同一底上的两个内角相等。 性质定理2 等腰梯形的两条对角线相等。 证明定理2:已知:(学生口述)
求证:(学生口述)思路:转化方向——全等三角形.已知:如图,在梯形ABCD中,AD∥BC ,AB=DC
求证:AC=BD
证明: ∵ AD∥BC ,AB=DC ,
∴∠ABC=∠DCB(等腰梯形在同一底上的两个内角相等)
∴ 在△ABC与△DCB中
∴ AB=CD
∠ABC=∠DCB
BC=CB
∴ △ABC≌△DCB.
∴AC=BD
等腰梯形中常用的辅助线:
E等腰梯形性质巩固练习2:对角线为4且互相垂直的等腰梯形面积____。 ACDBE自主探索:
等腰梯形是轴对称图形吗?
如何说理?方法的迁移O 如图,四边形ABCD是等腰梯形,腰AB=DC,AC、BD是它的对角线,它是轴对称图形吗?对称轴在哪里?你能发现哪些相等的线段和相等的角?等腰梯形是轴对称图形,上下底的中点的连线所在的直线是它的对称轴。两条对角线相等.两底平行,两腰相等.同一底边上的两个内角相等. 加油,成功在等你!
(含自主练习)自主小结试一试下列说法中正确的个数是( )(1)一组对边平行的四边形是梯形.(2)等腰梯形的对角线相等.(3)等腰梯形的两个内角相等.(4)等腰梯形有一条对称轴.A.1个 B.2个 C.3个 D.4个B等腰梯形性质运用练习: ①等腰梯形的一底角为 150°,腰长
为10,下底长为50,则上底长为____。
②链接生活(课后拓展)
花园地上铺着彩色的正方形地砖.除了用正方形的地砖铺之外,还可以用其他形状的地砖铺吗?用等腰梯形的地砖如何铺?画出你的设计.
提示:用两腰和上底相等且内角分别为60°和120°的等腰梯形来设计,如图)22.5(1)等腰梯形分层作业A :1、练习册:习题22.5(1)
2、预习 22.5(2)
3、完成方法三(证明性质1)
B: 1、画等腰梯形中常用的辅助线。
2、完成课后拓展题(铺地砖)分层布置(A必做、B选做)方法3:过点C作AB的平行线,
交AD的延长线于点E,则
四边形ABCE为平行四边形
∴AB=CE, ∠B=∠E,∠BCD=∠EDC
又∵AB=CD,
∴CE=CD, ∴∠EDC=∠E
∴∠B=∠BCD
ABDCE
长方形和等腰三角形都平放交叠在一起,重叠部分是什么形,为什么?要养成猜想后推理证明的习惯。你找到等腰梯形了吗?你找到等腰梯形了吗?你找到等腰梯形了吗?猜想等腰梯形有什么性质?
提示:从角考虑。 题设等腰梯形在同一底上的两个内角相等。结论22.5(1)等腰梯形性质 题设等腰梯形在同一底上的两个内角相等。结论等腰梯形性质 等腰梯形的性质已知:梯形ABCD中,AD // BC,AB = DC
求证: ∠B = ∠C
证明:过点D作DE // AB交BC于E
∵ AD // BC,∴ AB = DE
∵ AB = DC ,∴ DE = DC
∴∠1 =∠C
∵ DE // AB
∴ ∠1 = ∠B
∴ ∠B = ∠C
∠A = ∠CDA还要从新证起吗?
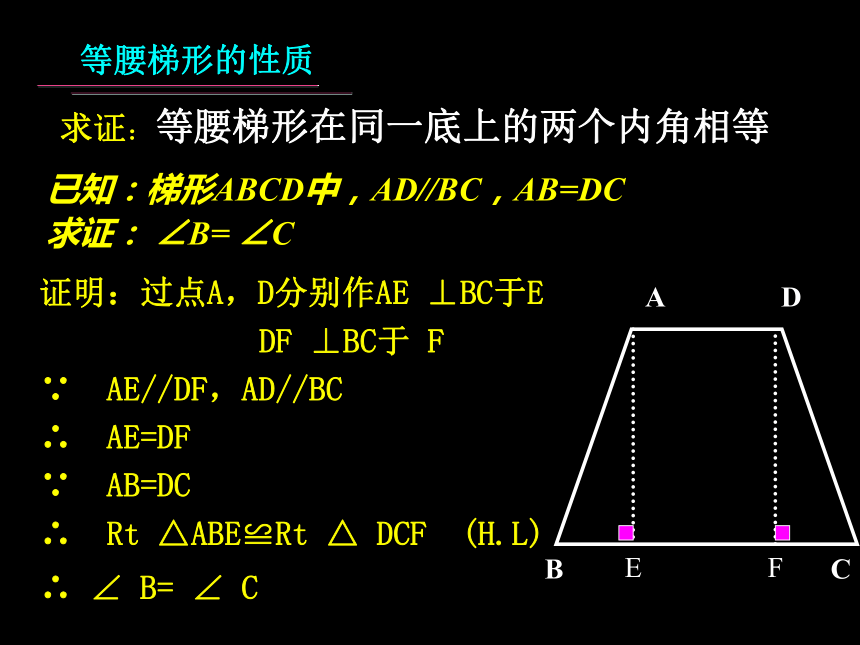
等腰梯形的性质证明:过点A,D分别作AE ⊥BC于E
DF ⊥BC于 F
∵ AE//DF,AD//BC
∴ AE=DF
∵ AB=DC
∴ Rt △ABE≌Rt △ DCF (H.L)
∴ ∠ B= ∠ C
已知:梯形ABCD中,AD//BC,AB=DC
求证: ∠B= ∠C
求证:等腰梯形在同一底上的两个内角相等等腰梯形的性质等腰梯形性质定理1:
等腰梯形在同一底上的两个内角相等已知:梯形ABCD中,AD//BC,AB=DC
求证: ∠B= ∠C
方法一:
方法二:等腰梯形的性质 等腰梯形性质定理1: 等腰梯形在同一底上的两个内角相等已知:梯形ABCD中,AD//BC,AB=DC
求证: ∠B= ∠C
方法三:
E请回家完成方法三
若还有新方法也请自行完成现已知等腰梯形,
求证上方是等腰三角形。操作:
长方形和等腰三角形都平放交叠在一起,重叠部分是什么形,为什么??例题1:已知:梯形ABCD中,AD//BC,腰BA和CD的延长线交于点E.
求证: △EAD是等腰三角形.证明 ∵四边形ABCD是等腰梯形, AD//BC ,
∴ ∠B= ∠C (等腰梯形在同一底上的两个内角相等)
∵ AD//BC
∴ ∠1= ∠B ,∠2= ∠C ,
∴ ∠1= ∠2
∴ △EAD是等腰三角形.
12新问题老问题等腰梯形三角形或特殊四边形转化转化学 有 所 获等腰梯形性质巩固练习1:如图,在等腰梯形ABCD中,
AD∥BC ,AD=AB,BD⊥DC,
求∠C的度数。 题设结论等腰梯形性质 等腰梯形的除了“等腰梯形在同一底上的两个内角相等”还有什么性质?提示:从对角线考虑。 题设结论等腰梯形性质 等腰梯形的两条对角线相等。等腰梯形的两条对角线相等。题设结论等腰梯形性质: ∴ AC=BD等腰梯形的性质定理:性质定理1 等腰梯形在同一底上的两个内角相等。 性质定理2 等腰梯形的两条对角线相等。 证明定理2:已知:(学生口述)
求证:(学生口述)思路:转化方向——全等三角形.已知:如图,在梯形ABCD中,AD∥BC ,AB=DC
求证:AC=BD
证明: ∵ AD∥BC ,AB=DC ,
∴∠ABC=∠DCB(等腰梯形在同一底上的两个内角相等)
∴ 在△ABC与△DCB中
∴ AB=CD
∠ABC=∠DCB
BC=CB
∴ △ABC≌△DCB.
∴AC=BD
等腰梯形中常用的辅助线:
E等腰梯形性质巩固练习2:对角线为4且互相垂直的等腰梯形面积____。 ACDBE自主探索:
等腰梯形是轴对称图形吗?
如何说理?方法的迁移O 如图,四边形ABCD是等腰梯形,腰AB=DC,AC、BD是它的对角线,它是轴对称图形吗?对称轴在哪里?你能发现哪些相等的线段和相等的角?等腰梯形是轴对称图形,上下底的中点的连线所在的直线是它的对称轴。两条对角线相等.两底平行,两腰相等.同一底边上的两个内角相等. 加油,成功在等你!
(含自主练习)自主小结试一试下列说法中正确的个数是( )(1)一组对边平行的四边形是梯形.(2)等腰梯形的对角线相等.(3)等腰梯形的两个内角相等.(4)等腰梯形有一条对称轴.A.1个 B.2个 C.3个 D.4个B等腰梯形性质运用练习: ①等腰梯形的一底角为 150°,腰长
为10,下底长为50,则上底长为____。
②链接生活(课后拓展)
花园地上铺着彩色的正方形地砖.除了用正方形的地砖铺之外,还可以用其他形状的地砖铺吗?用等腰梯形的地砖如何铺?画出你的设计.
提示:用两腰和上底相等且内角分别为60°和120°的等腰梯形来设计,如图)22.5(1)等腰梯形分层作业A :1、练习册:习题22.5(1)
2、预习 22.5(2)
3、完成方法三(证明性质1)
B: 1、画等腰梯形中常用的辅助线。
2、完成课后拓展题(铺地砖)分层布置(A必做、B选做)方法3:过点C作AB的平行线,
交AD的延长线于点E,则
四边形ABCE为平行四边形
∴AB=CE, ∠B=∠E,∠BCD=∠EDC
又∵AB=CD,
∴CE=CD, ∴∠EDC=∠E
∴∠B=∠BCD
ABDCE
