22.9(1) 平面向量的减法 课件(15张PPT)
文档属性
| 名称 | 22.9(1) 平面向量的减法 课件(15张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 610.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-14 00:00:00 | ||
图片预览

文档简介
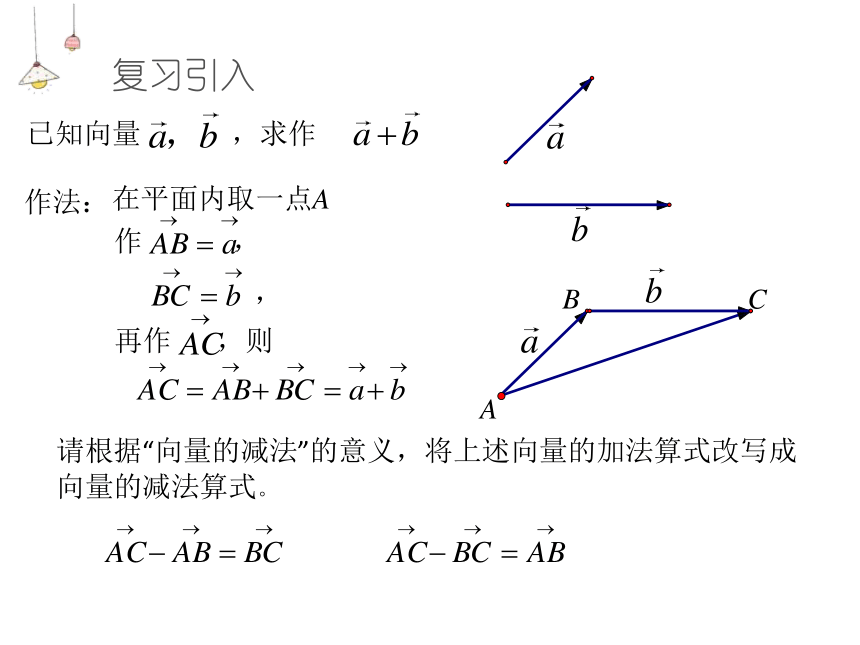
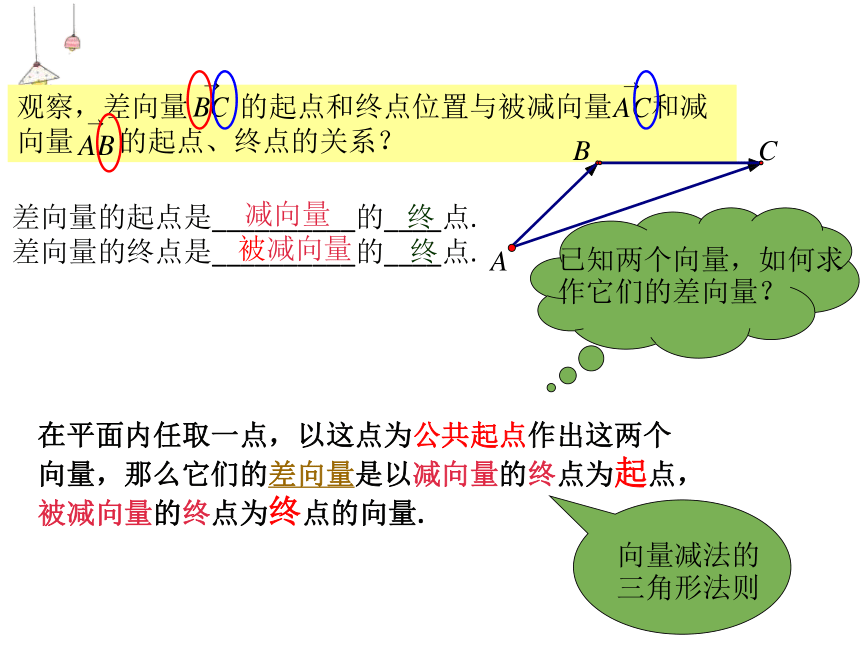
课件15张PPT。22.9(1) 平面向量的减法复习引入再作 ,则 作 , 作法:在平面内取一点A,ABC复习引入再作 ,则 作 , 作法:在平面内取一点A,ABC请根据“向量的减法”的意义,将上述向量的加法算式改写成向量的减法算式。ABC差向量的起点是__________的____点.
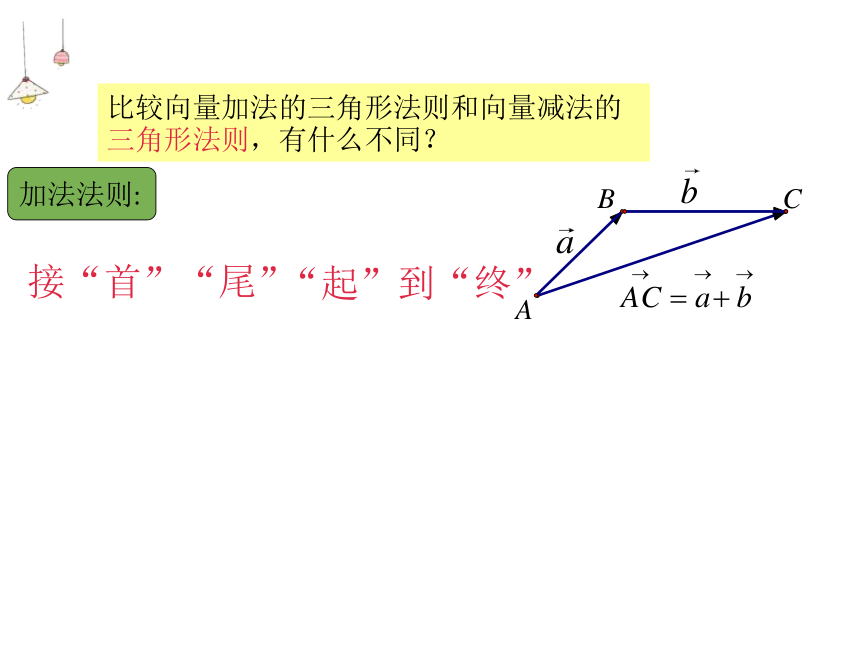
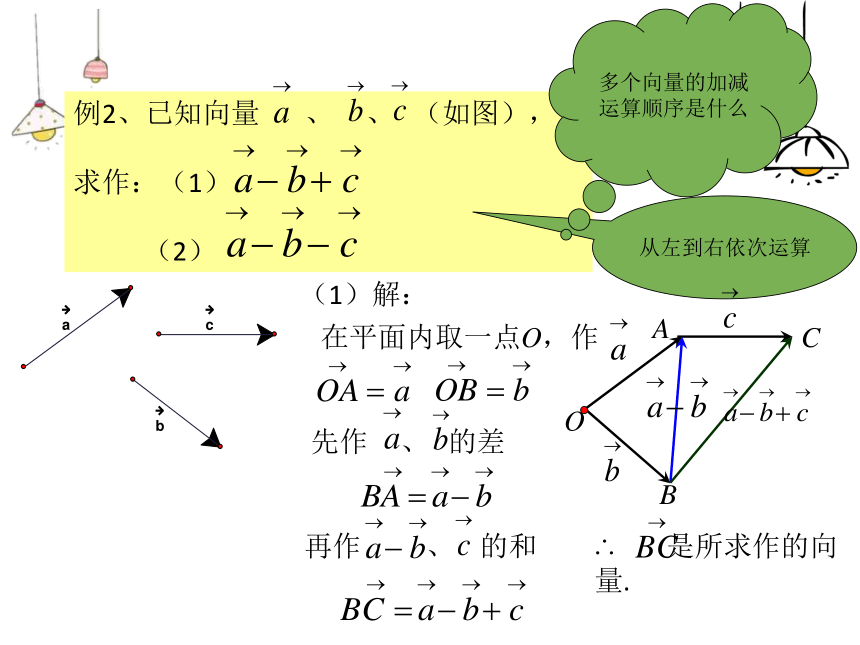
差向量的终点是__________的____点.减向量被减向量终终在平面内任取一点,以这点为公共起点作出这两个向量,那么它们的差向量是以减向量的终点为起点,被减向量的终点为终点的向量.比较向量加法的三角形法则和向量减法的三角形法则,有什么不同?ABC接“首”“尾”“起”到“终”从左到右依次运算(1)解:OBCA先作 、 的差再作 、 的和在平面内取一点O,作∴ 是所求作的向量.多个向量的加减
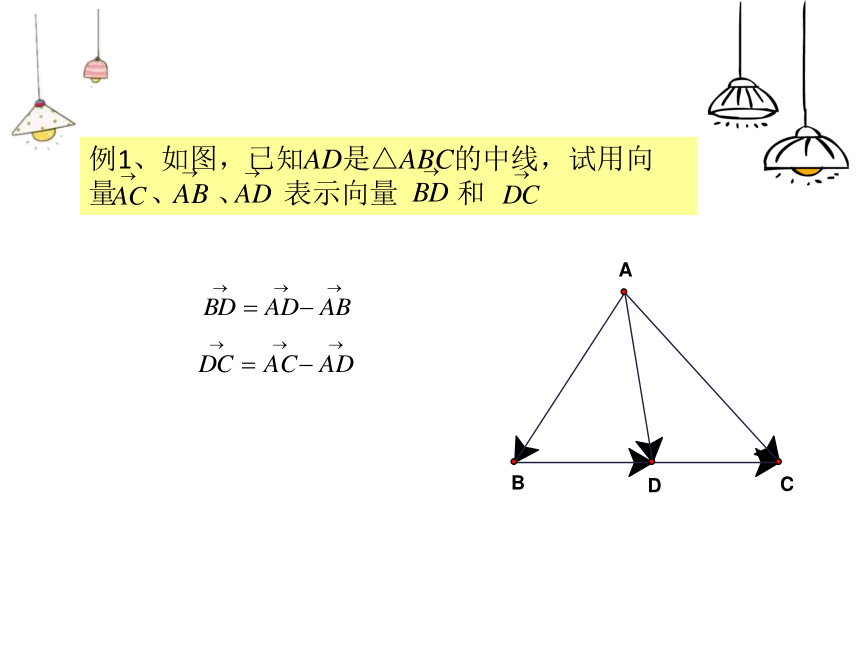
运算顺序是什么OBAC∴ 是所求作的向量.把向量的减法转化为加法在平面内取一点O,作(2)解:OBCA在平面内取一点O,作先作 、 的差再作 、 的差∴ 是所求作的向量.OBCA∴ 是所求作的向量.在平面内取一点O,作把向量的减法转化为加法课堂小结作业布置练习册22.9(1)1、如图,已知向量 、 ,求作 ∴ 是所求作的向量.还能怎样作?课堂练习课堂练习2、思考:不画图怎样直接计算:________________________________________________________“共”“起”点“减”到“被”向量减法的要领是什么?课堂练习____3、填空____
差向量的终点是__________的____点.减向量被减向量终终在平面内任取一点,以这点为公共起点作出这两个向量,那么它们的差向量是以减向量的终点为起点,被减向量的终点为终点的向量.比较向量加法的三角形法则和向量减法的三角形法则,有什么不同?ABC接“首”“尾”“起”到“终”从左到右依次运算(1)解:OBCA先作 、 的差再作 、 的和在平面内取一点O,作∴ 是所求作的向量.多个向量的加减
运算顺序是什么OBAC∴ 是所求作的向量.把向量的减法转化为加法在平面内取一点O,作(2)解:OBCA在平面内取一点O,作先作 、 的差再作 、 的差∴ 是所求作的向量.OBCA∴ 是所求作的向量.在平面内取一点O,作把向量的减法转化为加法课堂小结作业布置练习册22.9(1)1、如图,已知向量 、 ,求作 ∴ 是所求作的向量.还能怎样作?课堂练习课堂练习2、思考:不画图怎样直接计算:________________________________________________________“共”“起”点“减”到“被”向量减法的要领是什么?课堂练习____3、填空____
