重庆市主城区七校2018-2019学年高二上学期期末考试数学(文)试题
文档属性
| 名称 | 重庆市主城区七校2018-2019学年高二上学期期末考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 1014.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览




文档简介
2018——2019学年(上)期末考试
高2020级文科数学试题
一、选择题:(本大题共12小题,每小题5分,共60分.在每个小题的四个选项中,只有一项是符合题目要求的.)
1.已知直线的方程为x﹣y﹣4=0,则该直线的倾斜角为( )
A. B. C. D.π
2.命题“?x∈R,使x2+ax+1<0”的否定是( )
A.?x∈R,使x2+ax+1>0 B.?x∈R,使x2+ax+1≥0
C.?x∈R,x2+ax+1>0成立 D.?x∈R,x2+ax+1≥0成立
3.已知双曲线的虚轴长是实轴长的2倍,则实数m的值是( )
A.4 B. C. D.﹣4
4.已知函数f(x)=ex﹣cosx,则曲线f(x)在点(0,f(0))处的切线方程为( )
A.y=0 B.y=2x C.y=x D.y=﹣2x
5.如图是一个几何体的三视图,若它的体积是6,则a=( )
A.1 B. C.2 D.2
6.“k=8“是“圆O1:(x+1)2+(y﹣1)2=2与圆O2:(x﹣2)2+(y+2)2=k“相切的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.设m,n表示不同的直线,α,β表示不同的平面,给出下列命题,正确命题的个数为( )
①若α⊥β,m⊥α,则m∥β:
②若m⊥α,n⊥β,α∥β,则m∥n;
③若m⊥α,n⊥β,α⊥β,则m⊥n;
④若m?α,n?β,m⊥n,则α⊥β:
A.0个 B.1个 C.2个 D.3个
8.设抛物线C:y2=2px(p>0)的焦点为F,点M(m,4)在抛物线C上,且|MF|=5,则p的值为( )
A.4或8 B.2或4 C.2或8 D.4或16
9.若圆锥侧面展开图是圆心角为120°,半径为9的扇形,则这个圆锥的体积为( )
A.18π B.54π C.10π D.30元
10.定义在R上的可导函数f(x)的导函数为f'(x),已知函数y=ef'(x)的图象如图所示,则函数y=f(x)的单调递减区间为( )
A.(1,+∞) B.(1,e) C.(+∞,e) D.(e,+∞)
11.已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=AA1=2,BC=1,则异面直线AB1与BC1所成角弦值为( )
A. B. C. D.
12.已知函数f(x),若|f(x)|≥ax﹣1恒成立,则a的取值范围是( )
A.[﹣2,0] B.[﹣2,1] C.[﹣4,0] D.[﹣4,1]
二.填空题:(本大题共4小题,每小题5分,共20分,把答案填写在答题卡相应位置)
13.焦点在x轴上的椭圆方程为1,且离心率e,则实数k的值为 .
14.如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的表面积为S1,球O的表面积为S2,则的值是 .
15.若方程k(x﹣3)有两个不等实根,则实数k的取值范围为 .
16.已知双曲线C2与椭圆C1:1具有相同的焦点,则两条曲线相交的四个交点形成的四边形面积最大时,则双曲线C2的方程为 .
三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算
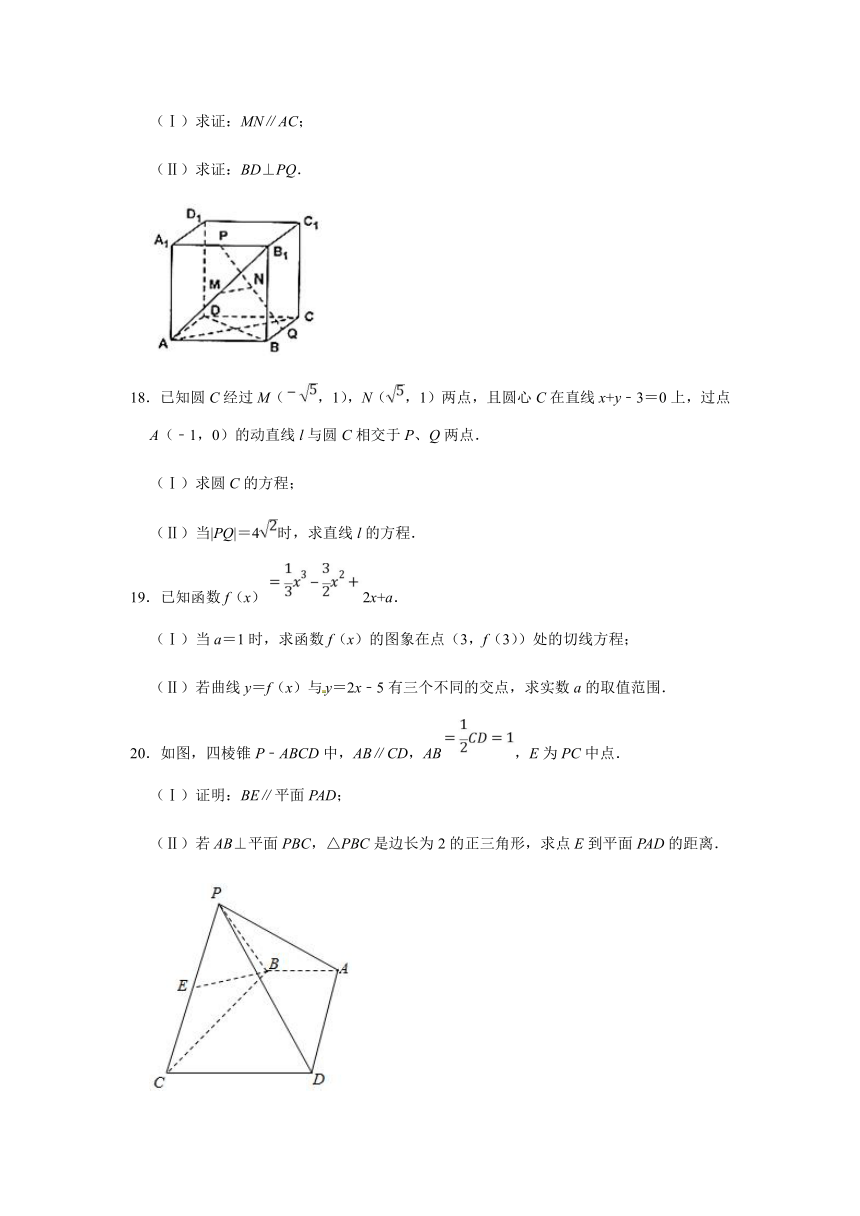
17.如图:在正方体ABCD﹣A1B1C1D1中,P、M、Q、N分别为线段A1B1、AB1、BC、PQ的中点.
(Ⅰ)求证:MN∥AC;
(Ⅱ)求证:BD⊥PQ.
18.已知圆C经过M(,1),N(,1)两点,且圆心C在直线x+y﹣3=0上,过点A(﹣1,0)的动直线l与圆C相交于P、Q两点.
(Ⅰ)求圆C的方程;
(Ⅱ)当|PQ|=4时,求直线l的方程.
19.已知函数f(x)2x+a.
(Ⅰ)当a=1时,求函数f(x)的图象在点(3,f(3))处的切线方程;
(Ⅱ)若曲线y=f(x)与y=2x﹣5有三个不同的交点,求实数a的取值范围.
20.如图,四棱锥P﹣ABCD中,AB∥CD,AB,E为PC中点.
(Ⅰ)证明:BE∥平面PAD;
(Ⅱ)若AB⊥平面PBC,△PBC是边长为2的正三角形,求点E到平面PAD的距离.
21.如图,P是圆x2+y2=4上的动点,P点在x轴上的射影是D,点M满足.
(Ⅰ)求动点M的轨迹C的方程
(Ⅱ)设A、B是轨迹C上的不同两点,点E(﹣4,0),且满足λ,若λ∈[,1),求直线AB的斜率k的取值范围.
22.已知函数f(x)=lnx(a∈R).
(Ⅰ)若函数f(x)在[1,+∞)上为增函数,求a的取值范围;
(Ⅱ)若函数g(x)=xf(x)ax2﹣x有两个不同的极值点x1,x2,证明.
一、选择题:(本大题共12小题,每小题5分,共60分.在每个小题的四个选项中,只有一项是符合题目要求的.)
1.B
2.D
3.A
4.C
5.D
6.A
7.C
8.C
9.A
10.D
11.C
12.C
二.填空题:(本大题共4小题,每小题5分,共20分,把答案填写在答题卡相应位置)
13.3.
14. .
15.(,0].
16.双曲线C2与椭圆C1:1具有相同的焦点,可得c,
两条曲线相交的四个交点形成四边形的面积最大,设在第一象限的交点为(m,n),可得S=4mn,
12mn,当且仅当mn时,mn,此时四边形的面积取得最大值,
解得m,n=1,
设双曲线的方程为1(a>0,b>0),
可得1,且a2+b2=2,解得a=b=1,
双曲线的方程为x2﹣y2=1.
三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算
17.证明:(Ⅰ)连接PM 并延长交AB于点E,连接EQ,
由题意可得M为线段PE的中点,
又N为线段PQ的中点,
所以MN∥EQ,
由题意可得E为线段AB的中点,
所以EQ∥AC,
所以MN∥AC;
(Ⅱ)由正方体可得BB1⊥平面ABCD,
由(Ⅰ)可知PE∥BB1,
所以PE⊥平面ABCD,
可得PE⊥BD,
又ABCD为正方形,
所以AC⊥BD,
所以EQ⊥BD,
又EQ∩PE=E,
所以BD⊥平面PEQ,
所以BD⊥PQ.
18.(Ⅰ)由圆C经过M(,1),N(,1)两点,则圆C关于y轴对称;
设圆心C为(0,b),由圆心C在直线x+y﹣3=0上,
得0+b﹣3=0,解得b=3;
所以圆C的半径为r=|CM|3,
所以圆C的方程为x2+(y﹣3)2=9;
(Ⅱ)①当直线l与x轴垂直时,易知直线l的方程为x=﹣1,符合题意;
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),即kx﹣y+k=0,
设PQ的中点为H,由|PQ|=4,则|CH|1,
由|CH|1,解得k,
所以直线l的方程为4x﹣3y+4=0;
综上知,直线l的方程为x=﹣1或4x﹣3y+4=0.
19.(I)∵f(x)2x+a,
∴f′(x)=x2﹣3x+2,
∴切线斜率k=f′(3)=2,f(3),
f(x)的图象在点(3,f(3))处的切线方程y2(x﹣3)即4x﹣2y﹣7=0,
(II)由题意可得,2x﹣52x+a,
整理可得,﹣a5有三个不同的实数根,
设g(x)5,则g′(x)=x2﹣3x,
当x∈(0,3)时,g′(x)<0,g(x)单调递减,
当x∈(﹣∞,0),(3,+∞)时,g′(x)>0,g(x)单调递增,
又g(0)=5,g(3),
故当x=0时,g(x)取得极大值5,当x=3时,g(x)取得极小值
作出函数g(x)的大致图象,结合图象可得,,
∴,
故a的范围(﹣5,).
20.证明:(Ⅰ)取PD的中点F,连结AF,EF.………(1分)
∵E为PC的中点,∴EF∥CD,且EF.
又∵AB∥CD,且AB,
∴EF∥AB,且EF=AB,故四边形ABEF为平行四边形.
∴BE∥AF.………………
又BE?平面BEP,AF?平面BEP,
∴BE∥平面PAD. ………………
解:(Ⅱ)由(Ⅰ)得BE∥平面PAD.
故点B到平面PAD的距离等于点E
到平面PAD的距离.………………(6分)
取BC的中点G,连结PG.………………(7分)
∵AB⊥平面PBC,AB?平面ABCD,
∴平面ABCD⊥平面PBC.
又△PBC是边长为2的正三角形,∴PG,BC=2,且PG⊥BC.
∵平面ABCD∩平面PBC=BC,∴PG⊥平面ABCD. ………………(9分)
∵四边形是直角梯形,AB=1,BC=2,CD=2,
∴AD,.
∵AB⊥PB,AB=1,PB=PC=2,CD=2,
∴PA,PD=2.
∴S△APD.………………
记点B到平面PAD的距离为h,
∵三棱锥P﹣ABD的体积V,
∴h.………………(11分)
∴点E到平面PAD的距离为.………………
21.(1)设M(x,y),则D(x,0),由,知P(x,2y),
∵点P在圆x2+y2=4上,
∴x2+4y2=4,故点M的轨迹C的方程为;
(2)根据题意,直线AB的斜率存在且不为0,不妨设直线AB:y=k(x+4),
联立,整理得(4)y2y+12=0,
则△=()2﹣48(4)>0,解得即k,
设A(x1,y1),B(x2,y2),
则根据韦达定理得y1+y2,y1y2,
又因为λ,即(x1+4,y1)=λ(x2+4,y2),
所以,从而,
消去y2得,
令φ(λ)λ2其中λ∈[,1),
则φ(λ)在[,1)上单调递减,即有φ(1)<φ(λ)≤φ(),
从而4<φ(λ),
所以4,解得即k或k,
综上,k∈(,]∪[,).
22.(I)∵f(x)=lnx,
∴f′(x),
∵f(x)在[1,+∞)上为增函数,
∴f′(x)在[1,+∞)上恒成立,
故a≤xmin=1,即a≤1,
(Ⅱ)证明:∵g(x)=xlnxax2﹣x+a有两个不同的极值点x1,x2,
∴g′(x)=lnx﹣ax有两个不同的零点x1,x2,
即,
∴lnx1+lnx2=a(x1+x2),
∴a,
同理可得,a,
∴,
,
令t,不防设x1<x2,则t∈(0,1),
∴,
原不等式等价于证tlnt,
令h(t)=lnt﹣t,则h′(t)0在(0,1)上恒成立,
故h(t)在(0,1)单调递减,h(t)>h(1)=0,
即.
