五年级下册数学课件-第3课时 平均数的再认识.北师大版(共18张PPT)
文档属性
| 名称 | 五年级下册数学课件-第3课时 平均数的再认识.北师大版(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
数学五年级
下册
第八单元
数据的分析和整理
第4课时 平均数的再认识
一、情景导入
同学们,请回忆一下我们前面学习过的平均数,你知道如何计算平均数吗?
(1)移多补少法;
(2)先把每个数加起,来,再除以总个数。
那么平均数与哪些因素有关呢?受哪些因素的影响较大呢?
今天就来进一步探究有 关平均数的问题。
二、探究新知
(1)用自己的语言说一说,1.2m这个数据可能是如何得到的呢?
1.结合生活实际探究问题。
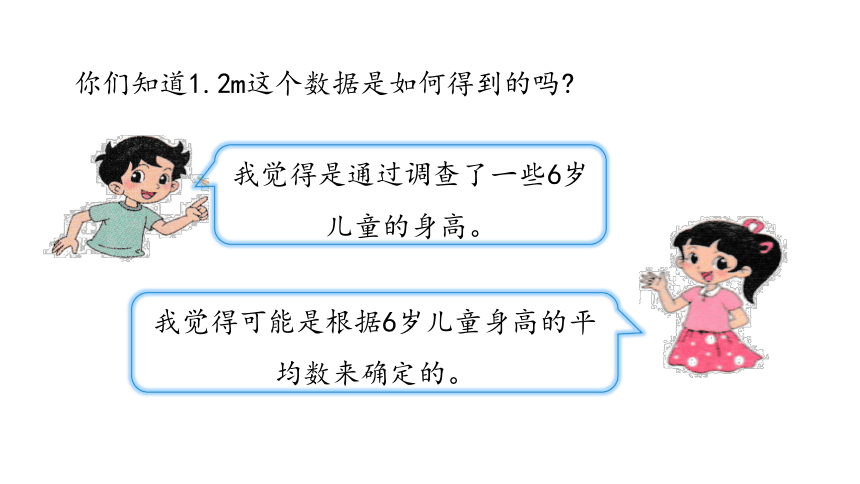
你们知道1.2m这个数据是如何得到的吗?
同学们的猜测到底对不对呢?下面我们来看一下北京市6岁儿童身高的统计数据,验证一下6岁儿童的身高是不是1.2m左右。
据统计,目前北京市6岁男童身高的平均值为119.3cm,女童身高的平均值为118.7cm。
通过比较,你发现了什么?
通过比较,你发现了什么?
小结:6岁以下的儿童还没有到读小学的年龄,所以乘车免费,通过测量6岁儿童的身高,确定身高1.2m以下的儿童免费乘车是比较合理的。
119.3cm和118.7cm都和1.2m很接近,所以1.2 m的高度是通过统计6岁儿童的身高得出的平均身高。
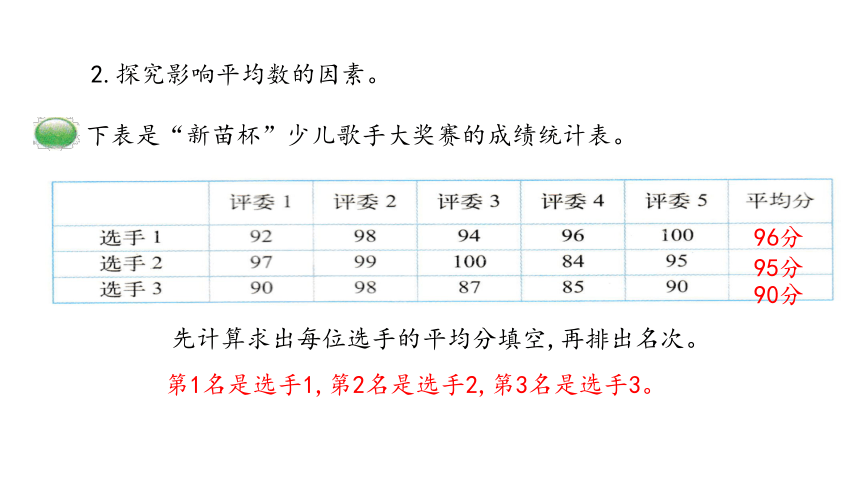
2.探究影响平均数的因素。
先计算求出每位选手的平均分填空,再排出名次。
96分
95分
90分
第1名是选手1,第2名是选手2,第3名是选手3。
在实际比赛中,通常都采取去掉一个最高分和一个最低分,然后再计算平均数的记分方法。你能说出其中的道理吗?
请同学们按照上述的方法重新计算3位选手的最终成绩,然后排出名次,看看所排出的名次和刚才排出的是否一样。
96分
97分
89分
第1名是选手2,第2名是选手1,第3名是选手3。
选手2为什么会变成第一名了呢?选手3的平均分又为什么下降了呢?
分析统计表中的数据,寻找原因,并在小组里说说自己的看法。
96分
97分
89分
3.平均数的再认识。
(1)通过刚才的探究,你对平均数有了哪些新的认识?
所以我们要灵活运用平均数,反映现实生活中的问题。
(2)小结:
有时一组数据的平均数能真实地反映某事件的一般情况;
有时,平均数因为个别数据的影响,变得不合理。
三、巩固练习
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是他们展开了调查。下面是他们调查时使用的评分标准。
(1)分别计算数学和英语喜欢程度的平均分。
数学:(1+4+5+2+4+3+2+1+5+3)÷10=3
英语:(2+4+4+2+2+3+1+1+3+2)÷10=2.6
(2)根据这些得分判断,对于这个组的学生,哪个科目更受欢迎?
答:数学平均分为3分,英语为2.6分。
答:数学更受欢迎。
2.淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
(1)计算这些小朋友的平均年龄。
(7+7+7+8+8+8+9+9)÷8≈8(岁)
答:这些小朋友的平均年龄是8岁。
2.淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
(2)这时,老师也加入做游戏的队伍。他的年龄是45岁,估计并计算此时做游戏的人的平均年龄。说一说你对平均数的认识。
(7+7+7+8+8+8+9+9+45)÷9=12(岁)
答:此时做游戏的人的平均年龄是12岁。
计算平均数时应该除去老师的年龄来计算平均数,老师与小朋友年龄相差较大,不具代表性。
3.学校举行歌唱比赛,8位老师给同一位同学的打分如下。
(7+7.2+7.5+8+8.4+9)÷6=7.85(分)
请采用一种方法给出这位同学合理的分数,并说出你的方法合理的理由。
答:去掉一个最高分和一个最低分。然后用剩余几个评委的平均分作为这位同学最后的成绩。因为有的评委打分太低或太高,去掉后再求平均分就更具有代表性。
4 7 7.2 7.5 8 8.4 9 9.8
四、课堂小结
通过本节课的学习,你对平均数又有了怎样的认识?和同学们讨论交流。
数学五年级
下册
第八单元
数据的分析和整理
第4课时 平均数的再认识
一、情景导入
同学们,请回忆一下我们前面学习过的平均数,你知道如何计算平均数吗?
(1)移多补少法;
(2)先把每个数加起,来,再除以总个数。
那么平均数与哪些因素有关呢?受哪些因素的影响较大呢?
今天就来进一步探究有 关平均数的问题。
二、探究新知
(1)用自己的语言说一说,1.2m这个数据可能是如何得到的呢?
1.结合生活实际探究问题。
你们知道1.2m这个数据是如何得到的吗?
同学们的猜测到底对不对呢?下面我们来看一下北京市6岁儿童身高的统计数据,验证一下6岁儿童的身高是不是1.2m左右。
据统计,目前北京市6岁男童身高的平均值为119.3cm,女童身高的平均值为118.7cm。
通过比较,你发现了什么?
通过比较,你发现了什么?
小结:6岁以下的儿童还没有到读小学的年龄,所以乘车免费,通过测量6岁儿童的身高,确定身高1.2m以下的儿童免费乘车是比较合理的。
119.3cm和118.7cm都和1.2m很接近,所以1.2 m的高度是通过统计6岁儿童的身高得出的平均身高。
2.探究影响平均数的因素。
先计算求出每位选手的平均分填空,再排出名次。
96分
95分
90分
第1名是选手1,第2名是选手2,第3名是选手3。
在实际比赛中,通常都采取去掉一个最高分和一个最低分,然后再计算平均数的记分方法。你能说出其中的道理吗?
请同学们按照上述的方法重新计算3位选手的最终成绩,然后排出名次,看看所排出的名次和刚才排出的是否一样。
96分
97分
89分
第1名是选手2,第2名是选手1,第3名是选手3。
选手2为什么会变成第一名了呢?选手3的平均分又为什么下降了呢?
分析统计表中的数据,寻找原因,并在小组里说说自己的看法。
96分
97分
89分
3.平均数的再认识。
(1)通过刚才的探究,你对平均数有了哪些新的认识?
所以我们要灵活运用平均数,反映现实生活中的问题。
(2)小结:
有时一组数据的平均数能真实地反映某事件的一般情况;
有时,平均数因为个别数据的影响,变得不合理。
三、巩固练习
1.一个10人小组想知道他们小组更喜欢数学还是英语,于是他们展开了调查。下面是他们调查时使用的评分标准。
(1)分别计算数学和英语喜欢程度的平均分。
数学:(1+4+5+2+4+3+2+1+5+3)÷10=3
英语:(2+4+4+2+2+3+1+1+3+2)÷10=2.6
(2)根据这些得分判断,对于这个组的学生,哪个科目更受欢迎?
答:数学平均分为3分,英语为2.6分。
答:数学更受欢迎。
2.淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
(1)计算这些小朋友的平均年龄。
(7+7+7+8+8+8+9+9)÷8≈8(岁)
答:这些小朋友的平均年龄是8岁。
2.淘气调查了操场上做游戏的小朋友的年龄情况:
7岁,7岁,7岁,8岁,8岁,8岁,9岁,9岁。
(2)这时,老师也加入做游戏的队伍。他的年龄是45岁,估计并计算此时做游戏的人的平均年龄。说一说你对平均数的认识。
(7+7+7+8+8+8+9+9+45)÷9=12(岁)
答:此时做游戏的人的平均年龄是12岁。
计算平均数时应该除去老师的年龄来计算平均数,老师与小朋友年龄相差较大,不具代表性。
3.学校举行歌唱比赛,8位老师给同一位同学的打分如下。
(7+7.2+7.5+8+8.4+9)÷6=7.85(分)
请采用一种方法给出这位同学合理的分数,并说出你的方法合理的理由。
答:去掉一个最高分和一个最低分。然后用剩余几个评委的平均分作为这位同学最后的成绩。因为有的评委打分太低或太高,去掉后再求平均分就更具有代表性。
4 7 7.2 7.5 8 8.4 9 9.8
四、课堂小结
通过本节课的学习,你对平均数又有了怎样的认识?和同学们讨论交流。
