22.8 平面向量的加法 课件(22张PPT)
文档属性
| 名称 | 22.8 平面向量的加法 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览







文档简介
课件22张PPT。§22.8平面向量的加法有向线段定义:规定了方向的线段. 画有向线段的一般步骤:(1)定比例尺;(2)取定其起点并以它为端点按指定方向画一条射线;(3)按比例尺确定的长度在所画射线上从端点开始截取一条线段;(4)在截得的线段的另一端点处画一个箭头. 起点终点起点起点终点终点复习引入1. 向量的定义:
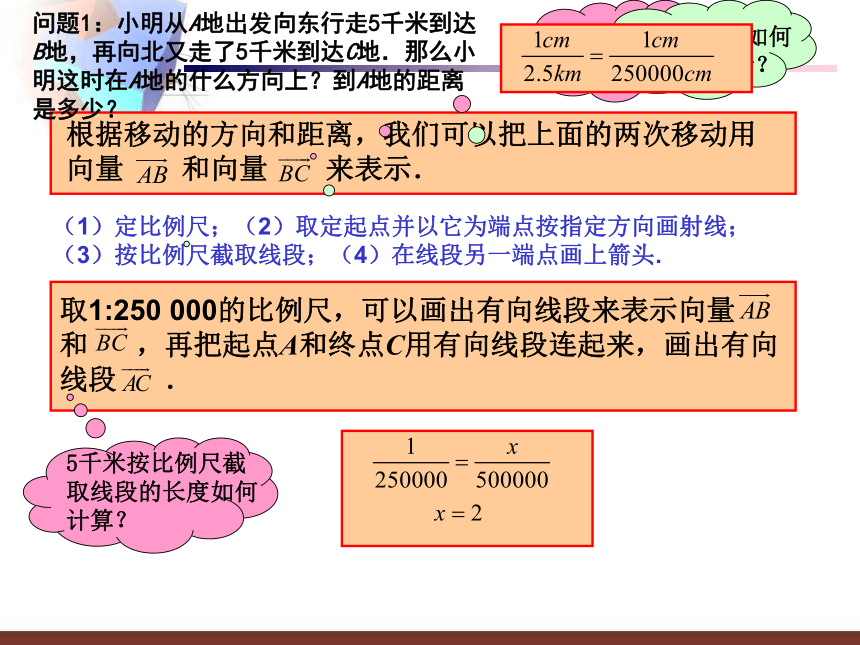
既有大小、又有方向的量叫做向量.2. 向量可以用有向线段表示:方向相同且长度相等的两个向量.方向相反且长度相等的两个向量. 方向相同或相反的两个向量. 探究新知问:长度、面积、体积在确定度量单位后,它们只有大小,可以用一个数来表示.这些量中的同一类量,都可以进行加减运算,而向量不仅有大小,还有方向,两个向量可以相加吗?这些量称为”数量”又称为“标量”探究新知问题1:小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?到A地的距离是多少?问1:小明从A地到达B地是不是一次位置移动?
从A移动到B的方向是什么?大小又是多少?是,以A为起点,方向是向东,大小是5千米.问2:从B地移动到C地是不是又是一次位置移动?方向是什么?大小又是多少?是,以B为起点,方向是向北,大小是5千米.根据移动的方向和距离,我们可以把上面的两次移动用向量 和向量 来表示. 如何画有向线段?(1)定比例尺;(2)取定起点并以它为端点按指定方向画射线;(3)按比例尺截取线段;(4)在线段另一端点画上箭头.取1:250 000的比例尺,可以画出有向线段来表示向量 和 ,再把起点A和终点C用有向线段连起来,画出有向线段 .5千米按比例尺截取线段的长度如何计算?5千米长度如何在纸上表示?问题1:小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?到A地的距离是多少?探究新知问3:那么这个向量 表示什么?表示以A为起点,A地到C地的一次位置移动.问4:如何计算 的大小和方向?由图可知:△ABC是直角三角形,∠B=90°AB=BC=5(千米),于是可得∠A=45°,AC= (千米),所以,向量 :东北方向从A地到B地,再从B地到C地这两次位置移动合在一起,其结果就是从A地到C地进行了一次位置移动,用向量来表示,就说“向量 与 合在一起是向量 ”,这时称 为 和 的和向量,可表示为 + = . 小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?A地的距离是多少?
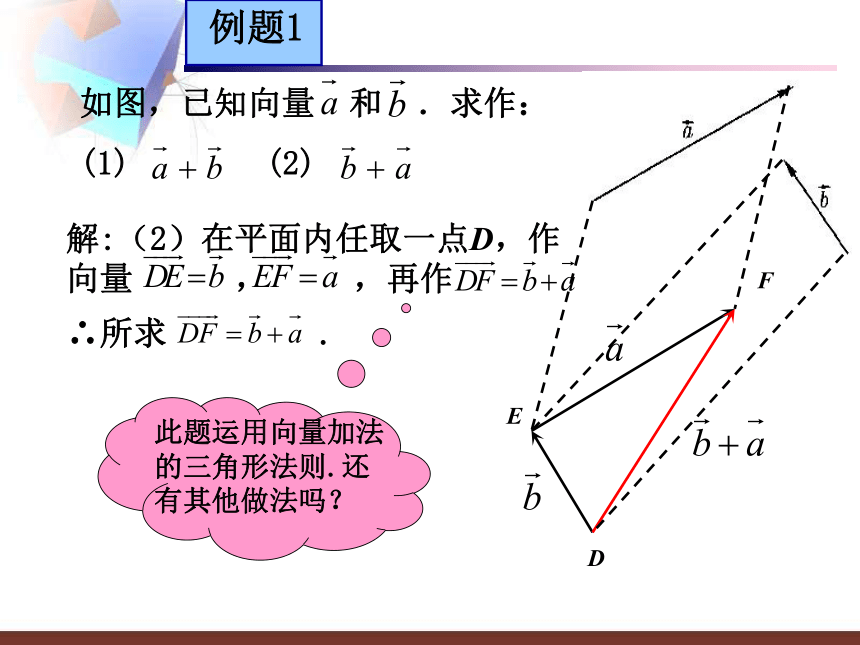
ABC北东向东行走5千米向北行走5千米探究新知定义:求两个向量的和向量的运算叫做向量的加法.问题2:已知向量 和 ,怎样求这两个向量的和向量?问:从问题1中我们可以得到启示,当我们把两个位置向量首尾相接时,它们的和向量很容易确定.但是我们如何把这两个向量首尾相接呢?可以通过平移的方法.O BA例题1如图,已知向量 和 .求作:
(1) (2)解:(2)在平面内任取一点D,作向量 , ,再作 ∴所求 . 此题运用向量加法的三角形法则.还有其他做法吗?DEF例题1如图,已知向量 和 .求作:
(1) (2)解法2:(2)以AB,BC为邻边,作平行四边形ABCD,再作向量 、 .∴所求 . 为什么?∵ABCD是平行四边形,
∴AD//BC,AD=BC;DC//AB;DC=AB.∴
得由此我们发现: = ,向量的加法满足交换律.ABCD1、如图,已知向量 , ,求作 (只要求画图表示,不必写作法)(1) (2) 巩固练习巩固练习2.如图,已知平行四边形ABCD,在图中作出下列两个向量的和向量.
(1) , ;(2) .(1) (2)∴ 是所求作的向量如何首尾相接?∴ 是所求作的向量运用向量加法的交换律∴ 是所求作的向量E探究新知问:如果不作图,你能否直接求出 ?练习:3.填空: = , = ,
= .能,第一条有向线段的终点恰好是第二条有向线段的起点(即首尾相接)AA例题2如图,已知向量 ,求作:
(1) ;
(2) 解:(1)在平面内任取一点O,作向量 , ,得 ;再作 ,然后作向量 ,则
请同学先试一试!(2)作向量 ,得 ,则 由此我们发现: ,向量的加法满足结合律.OABC你能先在题1的图形上找到 的和向量吗? 适时小结 由向量加法的交换律和结合律,可知三个向量相加,运算时可先将其中任意两个向量相加,所得的和向量再与第三个向量相加.
三个向量 、 、 相加,可表示为
. 探究新知 一般来说,求不平行的两个向量的和向量时,只要把第二个向量与第一个向量首尾相接,那么以第一个向量的起点为起点,第二个向量的终点为终点的向量就是和向量.这样的规定叫做向量加法的三角形法则.起点第一个向量终点和向量的起点和向量的终点第二个向量适时小结运用三角形法则的一般步骤:
1、画出表示第一个向量的有向线段;
2、以第一条有向线段的终点作为第二条有向线段的起点(即首尾相接);
3、以第一条有向线段的起点为起点,第二条有向线段的终点为终点画有向线段.探究新知问:如果给出两个平行的向量 和 ,那么如何求他们的和向量?两个平行向量也可像上面作图一样,此时,向量 、
、 在一条直线上,我们仍规定 .O ABO AB∴所求∴所求探究新知问:当 与 有特殊的关系时,它们的和向量是什么?当 与 是相等向量时, + = + =2 .当 与 是互为相反向量时, + = + = .00是向量吗?互为相反向量的两个向量的和是特殊的向量.
我们把长度为零的向量叫做零向量,记作 .规定 的方向可以是任意的(或者说不确定的); .于是,问:0和 的区别是什么?零向量有大小和方向,零只有大小;零向量的模是零.对于任意的向量,都有 , . 适时小结1.两个向量相加,结果一定还是向量;
2.零向量 和实数0的区别在于,零向量不仅表示大小是零,它还有方向,它的方向是任意的. 课堂小结 通过本节课的学习你得到了哪些新知识,又有哪些收获?1、三角形法则画向量的加法.
2、向量的加法也有交换律和结合律.
3、零向量和零是有区别的. 布置作业练习册习题22.8(1)
既有大小、又有方向的量叫做向量.2. 向量可以用有向线段表示:方向相同且长度相等的两个向量.方向相反且长度相等的两个向量. 方向相同或相反的两个向量. 探究新知问:长度、面积、体积在确定度量单位后,它们只有大小,可以用一个数来表示.这些量中的同一类量,都可以进行加减运算,而向量不仅有大小,还有方向,两个向量可以相加吗?这些量称为”数量”又称为“标量”探究新知问题1:小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?到A地的距离是多少?问1:小明从A地到达B地是不是一次位置移动?
从A移动到B的方向是什么?大小又是多少?是,以A为起点,方向是向东,大小是5千米.问2:从B地移动到C地是不是又是一次位置移动?方向是什么?大小又是多少?是,以B为起点,方向是向北,大小是5千米.根据移动的方向和距离,我们可以把上面的两次移动用向量 和向量 来表示. 如何画有向线段?(1)定比例尺;(2)取定起点并以它为端点按指定方向画射线;(3)按比例尺截取线段;(4)在线段另一端点画上箭头.取1:250 000的比例尺,可以画出有向线段来表示向量 和 ,再把起点A和终点C用有向线段连起来,画出有向线段 .5千米按比例尺截取线段的长度如何计算?5千米长度如何在纸上表示?问题1:小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?到A地的距离是多少?探究新知问3:那么这个向量 表示什么?表示以A为起点,A地到C地的一次位置移动.问4:如何计算 的大小和方向?由图可知:△ABC是直角三角形,∠B=90°AB=BC=5(千米),于是可得∠A=45°,AC= (千米),所以,向量 :东北方向从A地到B地,再从B地到C地这两次位置移动合在一起,其结果就是从A地到C地进行了一次位置移动,用向量来表示,就说“向量 与 合在一起是向量 ”,这时称 为 和 的和向量,可表示为 + = . 小明从A地出发向东行走5千米到达B地,再向北又走了5千米到达C地.那么小明这时在A地的什么方向上?A地的距离是多少?
ABC北东向东行走5千米向北行走5千米探究新知定义:求两个向量的和向量的运算叫做向量的加法.问题2:已知向量 和 ,怎样求这两个向量的和向量?问:从问题1中我们可以得到启示,当我们把两个位置向量首尾相接时,它们的和向量很容易确定.但是我们如何把这两个向量首尾相接呢?可以通过平移的方法.O BA例题1如图,已知向量 和 .求作:
(1) (2)解:(2)在平面内任取一点D,作向量 , ,再作 ∴所求 . 此题运用向量加法的三角形法则.还有其他做法吗?DEF例题1如图,已知向量 和 .求作:
(1) (2)解法2:(2)以AB,BC为邻边,作平行四边形ABCD,再作向量 、 .∴所求 . 为什么?∵ABCD是平行四边形,
∴AD//BC,AD=BC;DC//AB;DC=AB.∴
得由此我们发现: = ,向量的加法满足交换律.ABCD1、如图,已知向量 , ,求作 (只要求画图表示,不必写作法)(1) (2) 巩固练习巩固练习2.如图,已知平行四边形ABCD,在图中作出下列两个向量的和向量.
(1) , ;(2) .(1) (2)∴ 是所求作的向量如何首尾相接?∴ 是所求作的向量运用向量加法的交换律∴ 是所求作的向量E探究新知问:如果不作图,你能否直接求出 ?练习:3.填空: = , = ,
= .能,第一条有向线段的终点恰好是第二条有向线段的起点(即首尾相接)AA例题2如图,已知向量 ,求作:
(1) ;
(2) 解:(1)在平面内任取一点O,作向量 , ,得 ;再作 ,然后作向量 ,则
请同学先试一试!(2)作向量 ,得 ,则 由此我们发现: ,向量的加法满足结合律.OABC你能先在题1的图形上找到 的和向量吗? 适时小结 由向量加法的交换律和结合律,可知三个向量相加,运算时可先将其中任意两个向量相加,所得的和向量再与第三个向量相加.
三个向量 、 、 相加,可表示为
. 探究新知 一般来说,求不平行的两个向量的和向量时,只要把第二个向量与第一个向量首尾相接,那么以第一个向量的起点为起点,第二个向量的终点为终点的向量就是和向量.这样的规定叫做向量加法的三角形法则.起点第一个向量终点和向量的起点和向量的终点第二个向量适时小结运用三角形法则的一般步骤:
1、画出表示第一个向量的有向线段;
2、以第一条有向线段的终点作为第二条有向线段的起点(即首尾相接);
3、以第一条有向线段的起点为起点,第二条有向线段的终点为终点画有向线段.探究新知问:如果给出两个平行的向量 和 ,那么如何求他们的和向量?两个平行向量也可像上面作图一样,此时,向量 、
、 在一条直线上,我们仍规定 .O ABO AB∴所求∴所求探究新知问:当 与 有特殊的关系时,它们的和向量是什么?当 与 是相等向量时, + = + =2 .当 与 是互为相反向量时, + = + = .00是向量吗?互为相反向量的两个向量的和是特殊的向量.
我们把长度为零的向量叫做零向量,记作 .规定 的方向可以是任意的(或者说不确定的); .于是,问:0和 的区别是什么?零向量有大小和方向,零只有大小;零向量的模是零.对于任意的向量,都有 , . 适时小结1.两个向量相加,结果一定还是向量;
2.零向量 和实数0的区别在于,零向量不仅表示大小是零,它还有方向,它的方向是任意的. 课堂小结 通过本节课的学习你得到了哪些新知识,又有哪些收获?1、三角形法则画向量的加法.
2、向量的加法也有交换律和结合律.
3、零向量和零是有区别的. 布置作业练习册习题22.8(1)
