22.7(2) 平面向量 课件(23张PPT)
文档属性
| 名称 | 22.7(2) 平面向量 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 09:34:21 | ||
图片预览







文档简介
课件23张PPT。22.7(2) 平面向量复习引入
问题:1.已知:点A与点O的距离等于5cm,能不能由点O唯一确定A的位置吗?
2.已知:点A在点O的北偏东60°的方向,能不能由点O唯一确定A的位置吗?
3.已知:点A在点O的北偏东60°方向的5cm处,能不能由点O唯一确定A的位置吗?
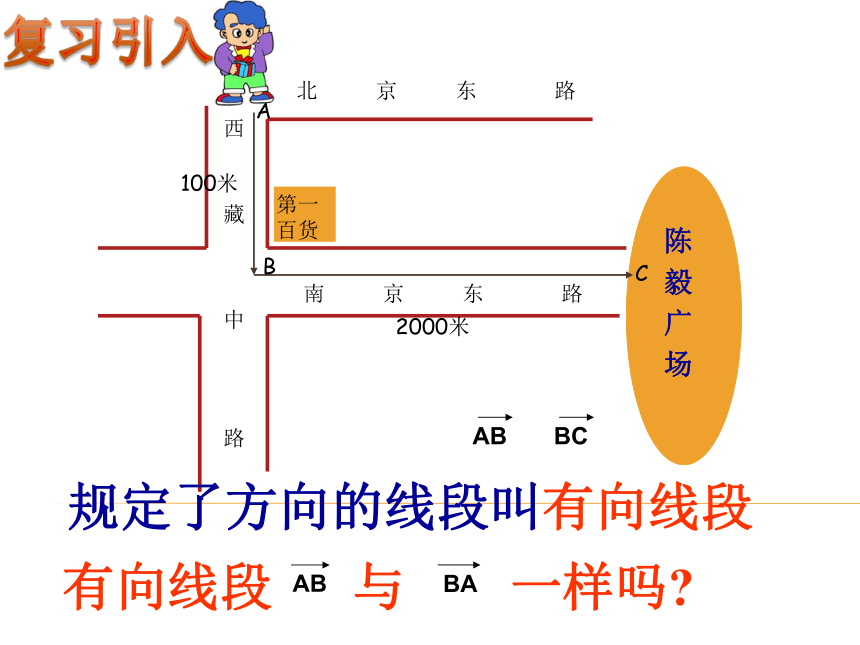
西 藏 中 路南 京 东 路北 京 东 路陈 毅 广 场100米2000米第一百货ACB规定了方向的线段叫有向线段 复习引入
2、既有大小又有方向的量叫做向量.向量的定义 1、 由以上的讨论可以看出,世界上确实存在着“既有大小、又有方向的量” . 表明我们有必要对这种量进行学习和研究.新课探索向量应该怎样表示呢? 想一想?新课探索向量的表示:1、向量可以用有向线段直观表示:
①有向线段的长度表示向量的长度(模);
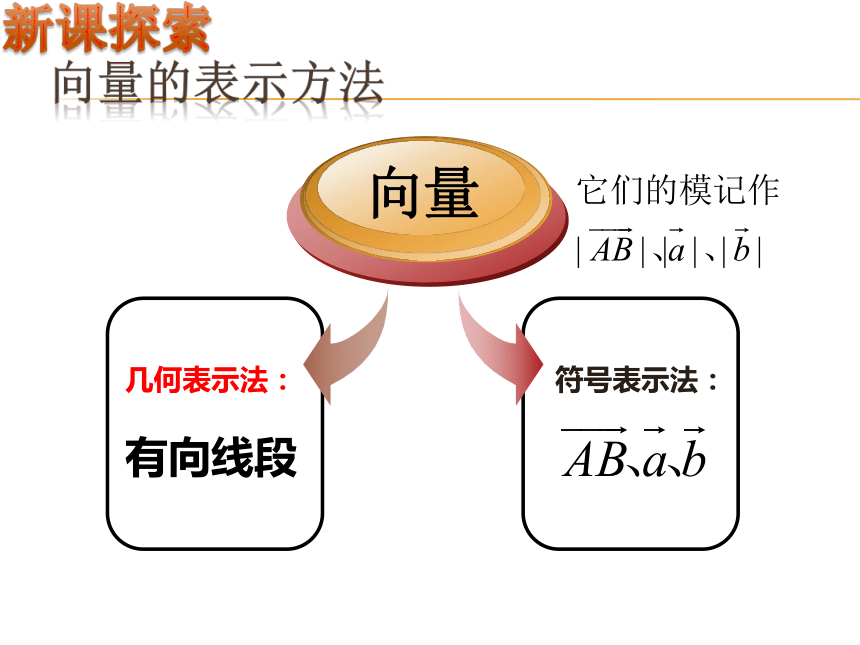
②有向线段的方向表示向量的方向。符号表示几何表示新课探索 向量的表示方法符号表示法:几何表示法:
有向线段向量新课探索既有大小、又有方向的量叫做向量.
数量与向量的区别:
数量:只有大小,是一个代数量,
可以比较大小
向量:有方向、大小的双重性,
不能比较大小
新课探索向量又称为矢量,最初被应用于物理学.很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量.大约公元前350年前,古希腊著名学者亚里士多德就知道了力可以表示成向量.最先使用有向线段表示向量的是英国科学家牛顿. 小知识:向量间的关系(1)用符号表示各个向量;如图,已知梯形ABCD中,AD∥BC,AB=DC,DE∥AB,点E在BC上。如果把图中线段都画成有向线段,那么在这些有向线段表示的向量中,指出(用符号表示):(2)平行四边形对边上的
两个向量,它们的方向
是相同还是相反?它们
的长度是否相等?新课探索向量间的关系方向相同且长度相等的两个向量叫做相等的向量.新课探索方向相反且长度相等的两个向量叫做互为相反向量.向量间的关系新课探索方向相同或相反的两个向量叫做平行向量向量间的关系新课探索想一想:新课探索向量 与 是什么关系的向量?
用符号表示出来.用有向线段表示的两个向量,如果两条有向线段分别所在的直线平行(或重合),那么这两个向量的方向相同或相反(平行向量).反之也成立.小提示新课探索讨论:两条直线平行与两个向量平行的异同?(1)当两个向量平行时,这两个向量所在的直线平行或重合.
(2)在直线平行的概念中,平行与重合是两个互不相容的概念,即互相重合的两条直线不能作为互相平行的直线,互相平行的两条直线一定不重合.新课探索判断题(1)平行向量的方向一定相同;
(2)不相等的向量一定不平行;
(3)若两个向量在同一直线上,则这两个向量一定是平行向量;
(4)相等向量一定是平行向量;
(5)平行向量一定是相等向量;课内练习简答题如图所示,四边形ABCD是正方形,图中有向线段都表示向量.课内练习已知△ABC和点P,如图,以点P为起点,分别画有向线段表示下列向量:新课探索操作课堂小结向量定义表示向量的有关概念几何表示法符号表示法向量的长度向量间的关系相等向量相反向量平行向量课堂小结本节课你有什么收获?作业布置校本:22.7(2)谢谢聆听!
问题:1.已知:点A与点O的距离等于5cm,能不能由点O唯一确定A的位置吗?
2.已知:点A在点O的北偏东60°的方向,能不能由点O唯一确定A的位置吗?
3.已知:点A在点O的北偏东60°方向的5cm处,能不能由点O唯一确定A的位置吗?
西 藏 中 路南 京 东 路北 京 东 路陈 毅 广 场100米2000米第一百货ACB规定了方向的线段叫有向线段 复习引入
2、既有大小又有方向的量叫做向量.向量的定义 1、 由以上的讨论可以看出,世界上确实存在着“既有大小、又有方向的量” . 表明我们有必要对这种量进行学习和研究.新课探索向量应该怎样表示呢? 想一想?新课探索向量的表示:1、向量可以用有向线段直观表示:
①有向线段的长度表示向量的长度(模);
②有向线段的方向表示向量的方向。符号表示几何表示新课探索 向量的表示方法符号表示法:几何表示法:
有向线段向量新课探索既有大小、又有方向的量叫做向量.
数量与向量的区别:
数量:只有大小,是一个代数量,
可以比较大小
向量:有方向、大小的双重性,
不能比较大小
新课探索向量又称为矢量,最初被应用于物理学.很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量.大约公元前350年前,古希腊著名学者亚里士多德就知道了力可以表示成向量.最先使用有向线段表示向量的是英国科学家牛顿. 小知识:向量间的关系(1)用符号表示各个向量;如图,已知梯形ABCD中,AD∥BC,AB=DC,DE∥AB,点E在BC上。如果把图中线段都画成有向线段,那么在这些有向线段表示的向量中,指出(用符号表示):(2)平行四边形对边上的
两个向量,它们的方向
是相同还是相反?它们
的长度是否相等?新课探索向量间的关系方向相同且长度相等的两个向量叫做相等的向量.新课探索方向相反且长度相等的两个向量叫做互为相反向量.向量间的关系新课探索方向相同或相反的两个向量叫做平行向量向量间的关系新课探索想一想:新课探索向量 与 是什么关系的向量?
用符号表示出来.用有向线段表示的两个向量,如果两条有向线段分别所在的直线平行(或重合),那么这两个向量的方向相同或相反(平行向量).反之也成立.小提示新课探索讨论:两条直线平行与两个向量平行的异同?(1)当两个向量平行时,这两个向量所在的直线平行或重合.
(2)在直线平行的概念中,平行与重合是两个互不相容的概念,即互相重合的两条直线不能作为互相平行的直线,互相平行的两条直线一定不重合.新课探索判断题(1)平行向量的方向一定相同;
(2)不相等的向量一定不平行;
(3)若两个向量在同一直线上,则这两个向量一定是平行向量;
(4)相等向量一定是平行向量;
(5)平行向量一定是相等向量;课内练习简答题如图所示,四边形ABCD是正方形,图中有向线段都表示向量.课内练习已知△ABC和点P,如图,以点P为起点,分别画有向线段表示下列向量:新课探索操作课堂小结向量定义表示向量的有关概念几何表示法符号表示法向量的长度向量间的关系相等向量相反向量平行向量课堂小结本节课你有什么收获?作业布置校本:22.7(2)谢谢聆听!
