22.7(2) 平面向量 课件(24张PPT)
文档属性
| 名称 | 22.7(2) 平面向量 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 460.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览







文档简介
课件24张PPT。22.7 平面向量第四节 平面向量及其加减法试一试: 在上新课之前,
谈谈你对向量的了解!
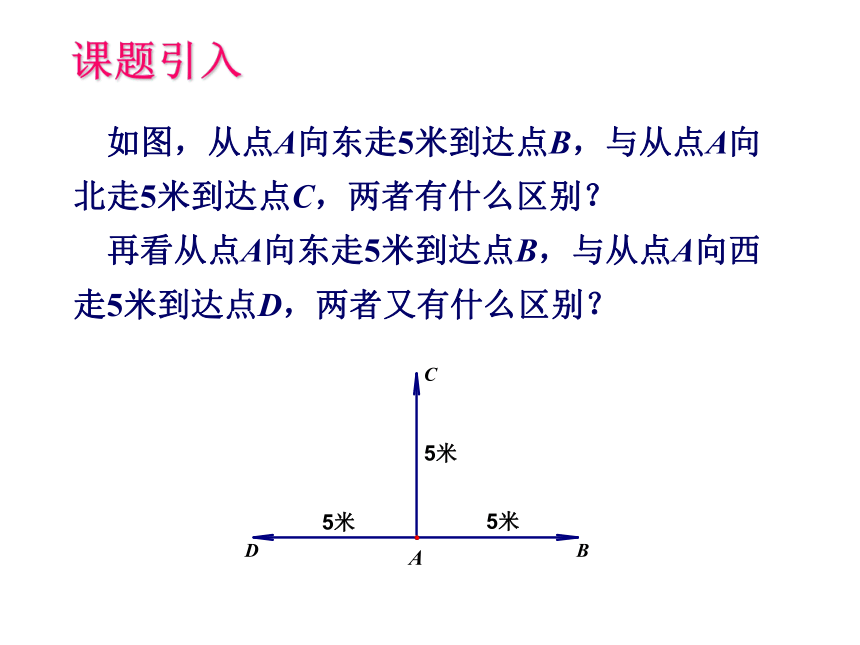
越多越好哟! 如图,从点A向东走5米到达点B,与从点A向北走5米到达点C,两者有什么区别?
再看从点A向东走5米到达点B,与从点A向西走5米到达点D,两者又有什么区别? 课题引入5米5米5米既有大小、又有方向的量叫做向量(vector) .
向量的定义 由以上的讨论可以看出,世界上确实存在着“既有大小、又有方向的量” . 表明我们有必要对这种量进行学习和研究.5米5米5米向量的表示方法 始点 A和终点 B间的距离表示向量
的大小,称为向量的模,记作 ; 图中向量可表示为:有向线段 ,其中 A为始点,B为终点. 比较:线段 与线段 一样吗?向量 与向量 一样吗?自始点 A指向终点 B的方向表示向量的方向. 向量还可以用小写的粗体英文字母表示,如 a、b、c、…;手写时,在字母上方加箭头,如 、 、 、…(见下图),它们的模分别
记作 、 、 、… .
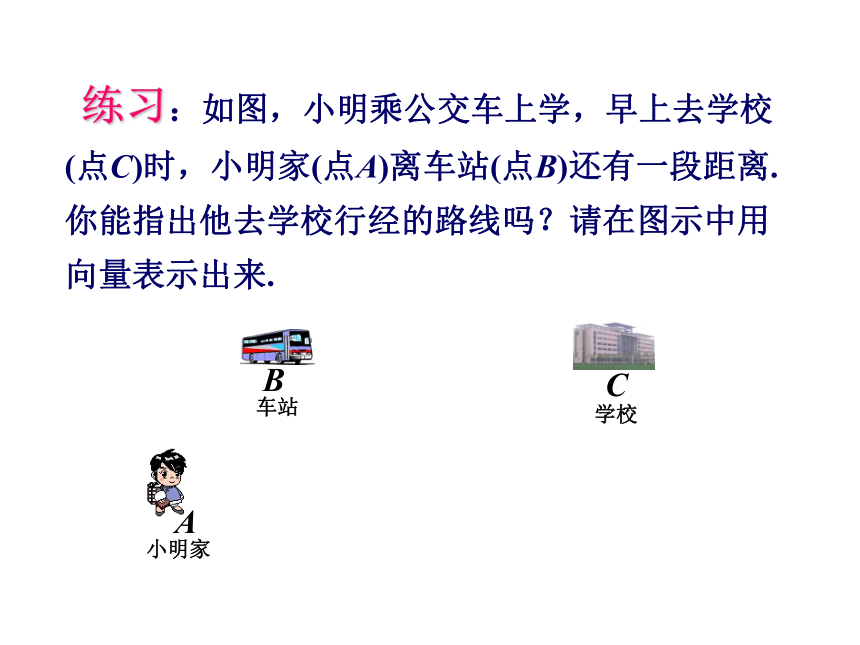
向量的表示方法 小明家车站学校ABC 练习:如图,小明乘公交车上学,早上去学校
(点C)时,小明家(点A)离车站(点B)还有一段距离.
你能指出他去学校行经的路线吗?请在图示中用向量表示出来.···ABC 练习:如图,小明乘公交车上学,早上去学校
(点C)时,小明家(点A)离车站(点B)还有一段距离.
你能指出他去学校行经的路线吗?请在图示中用向量表示出来.位移概念 在机械运动中,描述物体(质点)位置变化的物理量叫做位移. 显然位移是向量,是最简明、最易了解的向量之一. 位移概念 如物体在一圆周上作圆周运动(如图),从圆上点A出发,沿圆周运动到圆上另一点B,那么在这一运动过程中的位移为向量 ,它与物体运动的路径无关. AB 如果物体再从点B运动到圆上另一点C,则这一运动过程中的位移为向量 . 这与物体沿什么途径从点B运动到点C无关.
位移概念CAB位移概念 又如从圆上的点 A出发运动到圆上的点D(为过点A的直径的另一端点),则这个运动过程中的位移为 ,其模为圆的直径之长 .
DCAB位移概念由于位移只由始点和终点确定,与运动的路径无关,所以应用起来特别方便.
DCAB 除了位移之外,物理中的力、加速度、速度、磁场强度等(如图示)都是向量. 它们的用处很广泛. 向量的广泛意义起点固定的向量称为位置向量. 而数学中通常我们所研究的向量只含有大小和方向,可以自由作平行移动,我们称之为自由向量.例1 如图,□ABCD和梯形EFGH中,EF∥GH, 图中有向线段都表示向量,它们的起点和终点分别是所在四边形的顶点.
(1)用符号表示各个向量;例题讲解例1 如图,□ABCD和梯形EFGH中,EF∥GH, 图中有向线段都表示向量,它们的起点和终点分别是所在四边形的顶点.
(2)每个四边形的对边上的两个向量,它们的方向如何?它们的长度是否相等?例题讲解相等向量、相反向量和平行向量方向相同且长度相等的两个向量叫做相等的向量. 方向相反且长度相等的两个向量叫做互为相反的向量. 方向相同或相反的两个向量叫做平行向量. 思考:向量 与向量 是什么关系的向量?试用符号表示出来. 例题讲解例2 如图,△ABC和是等边三角形,D、E、F分别是各边中点. 在图中标有的向量中找出:
(1)相等向量;(2)相反向量;(3)平行向量.下图是由一根铁丝围成的正方形ABCD,在点A处有一只小虫. (1)如果小虫想要爬到点C处, 它有几种不同的走法, 用向量分别表示出来,并指出图中相等的向量;拓展练习 (2)如果正方形ABCD是一个桌面,小虫还有怎样的走法,最快的走法是什么?拓展练习 (3)在上述不同的走法中,小虫自 A到C的过程中的位移是什么?有哪几种不同的表示方法?由此,你发现了什么?拓展练习 课时小结 通过本节课的学习与探索,现在请你谈谈你对向量的了解.越多越好哟!
知识结构布置作业再见!1、课本P106 练习22.7
2、练习册P53习题22.7
谈谈你对向量的了解!
越多越好哟! 如图,从点A向东走5米到达点B,与从点A向北走5米到达点C,两者有什么区别?
再看从点A向东走5米到达点B,与从点A向西走5米到达点D,两者又有什么区别? 课题引入5米5米5米既有大小、又有方向的量叫做向量(vector) .
向量的定义 由以上的讨论可以看出,世界上确实存在着“既有大小、又有方向的量” . 表明我们有必要对这种量进行学习和研究.5米5米5米向量的表示方法 始点 A和终点 B间的距离表示向量
的大小,称为向量的模,记作 ; 图中向量可表示为:有向线段 ,其中 A为始点,B为终点. 比较:线段 与线段 一样吗?向量 与向量 一样吗?自始点 A指向终点 B的方向表示向量的方向. 向量还可以用小写的粗体英文字母表示,如 a、b、c、…;手写时,在字母上方加箭头,如 、 、 、…(见下图),它们的模分别
记作 、 、 、… .
向量的表示方法 小明家车站学校ABC 练习:如图,小明乘公交车上学,早上去学校
(点C)时,小明家(点A)离车站(点B)还有一段距离.
你能指出他去学校行经的路线吗?请在图示中用向量表示出来.···ABC 练习:如图,小明乘公交车上学,早上去学校
(点C)时,小明家(点A)离车站(点B)还有一段距离.
你能指出他去学校行经的路线吗?请在图示中用向量表示出来.位移概念 在机械运动中,描述物体(质点)位置变化的物理量叫做位移. 显然位移是向量,是最简明、最易了解的向量之一. 位移概念 如物体在一圆周上作圆周运动(如图),从圆上点A出发,沿圆周运动到圆上另一点B,那么在这一运动过程中的位移为向量 ,它与物体运动的路径无关. AB 如果物体再从点B运动到圆上另一点C,则这一运动过程中的位移为向量 . 这与物体沿什么途径从点B运动到点C无关.
位移概念CAB位移概念 又如从圆上的点 A出发运动到圆上的点D(为过点A的直径的另一端点),则这个运动过程中的位移为 ,其模为圆的直径之长 .
DCAB位移概念由于位移只由始点和终点确定,与运动的路径无关,所以应用起来特别方便.
DCAB 除了位移之外,物理中的力、加速度、速度、磁场强度等(如图示)都是向量. 它们的用处很广泛. 向量的广泛意义起点固定的向量称为位置向量. 而数学中通常我们所研究的向量只含有大小和方向,可以自由作平行移动,我们称之为自由向量.例1 如图,□ABCD和梯形EFGH中,EF∥GH, 图中有向线段都表示向量,它们的起点和终点分别是所在四边形的顶点.
(1)用符号表示各个向量;例题讲解例1 如图,□ABCD和梯形EFGH中,EF∥GH, 图中有向线段都表示向量,它们的起点和终点分别是所在四边形的顶点.
(2)每个四边形的对边上的两个向量,它们的方向如何?它们的长度是否相等?例题讲解相等向量、相反向量和平行向量方向相同且长度相等的两个向量叫做相等的向量. 方向相反且长度相等的两个向量叫做互为相反的向量. 方向相同或相反的两个向量叫做平行向量. 思考:向量 与向量 是什么关系的向量?试用符号表示出来. 例题讲解例2 如图,△ABC和是等边三角形,D、E、F分别是各边中点. 在图中标有的向量中找出:
(1)相等向量;(2)相反向量;(3)平行向量.下图是由一根铁丝围成的正方形ABCD,在点A处有一只小虫. (1)如果小虫想要爬到点C处, 它有几种不同的走法, 用向量分别表示出来,并指出图中相等的向量;拓展练习 (2)如果正方形ABCD是一个桌面,小虫还有怎样的走法,最快的走法是什么?拓展练习 (3)在上述不同的走法中,小虫自 A到C的过程中的位移是什么?有哪几种不同的表示方法?由此,你发现了什么?拓展练习 课时小结 通过本节课的学习与探索,现在请你谈谈你对向量的了解.越多越好哟!
知识结构布置作业再见!1、课本P106 练习22.7
2、练习册P53习题22.7
