20.1 一次函数的概念 课件(20张PPT)
文档属性
| 名称 | 20.1 一次函数的概念 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 370.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 09:40:02 | ||
图片预览






文档简介
课件20张PPT。§20.1一次函数的概念 一、复习引入1、什么是正比例函数?答:形如 y=kx(k≠0)的函数叫做正比例函数..2、正比例函数的图像是什么?答:正比例函数y=kx(k≠0)的图像是经过原点和(1,k)的一条直线.3、正比例函数有哪些性质? y随x 的增大而增大,图像经过 第 一、三象限; y随 x的增大而减小,图像经过
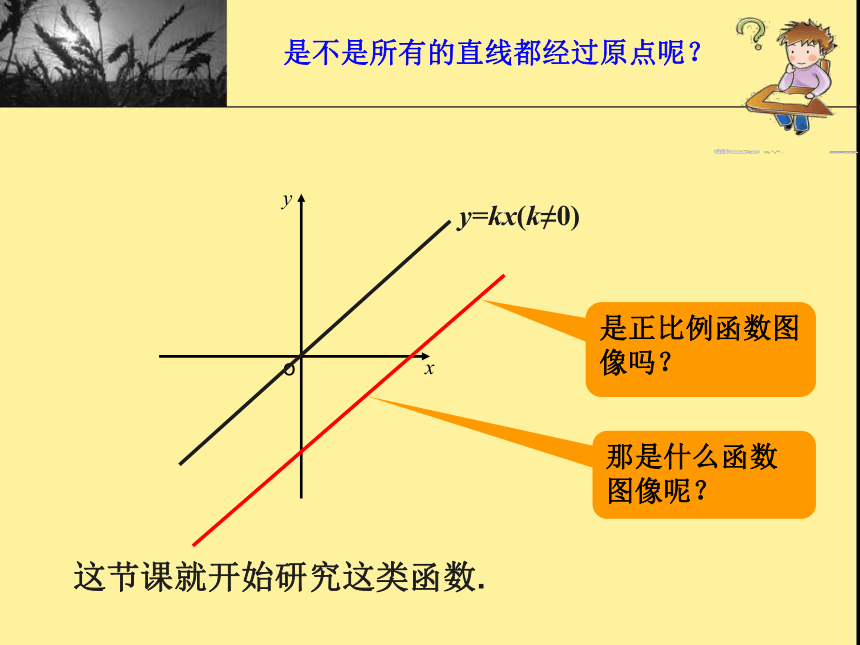
第 二、四象限.是不是所有的直线都经过原点呢?oy=kx(k≠0)是正比例函数图像吗?这节课就开始研究这类函数.那是什么函数图像呢?二、概念研究问题1:
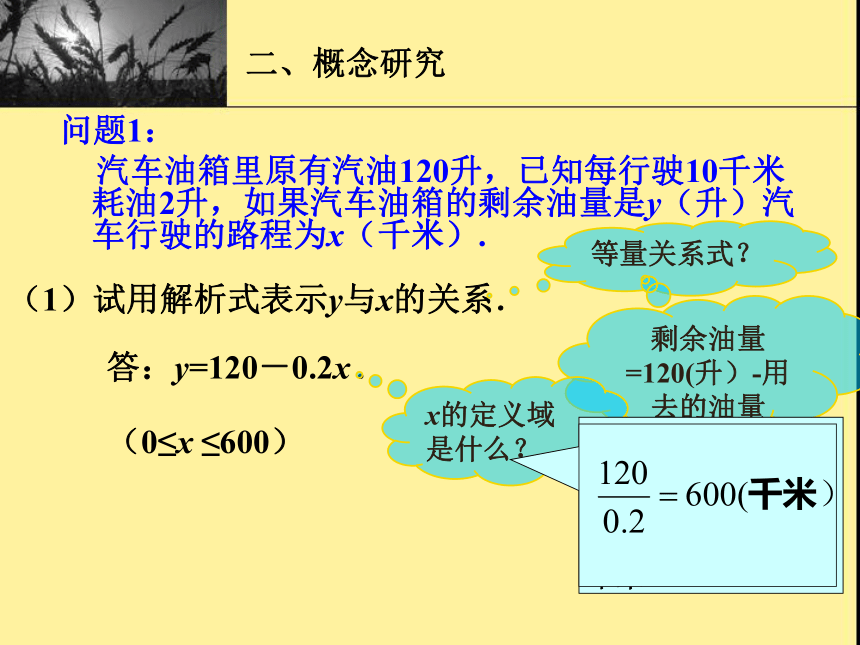
汽车油箱里原有汽油120升,已知每行驶10千米耗油2升,如果汽车油箱的剩余油量是y(升)汽车行驶的路程为x(千米). (1)试用解析式表示y与x的关系. 等量关系式?剩余油量=120(升)-用去的油量答:y=120-0.2x .x的定义域是什么?每行驶10千米耗油2升,就是每千米0.2升,那么120升汽油最远可以行驶多少千米? (0≤x ≤600)二、概念研究问题1:
汽车油箱里原有汽油120升,已知每行驶10千米耗油2升,如果汽车油箱的剩余是y(升)汽车行驶的路程为x(千米). (1)试用解析式表示y与x的关系. 答:y=120-0.2x (2)这个函数与正比例函数有何不同?答:y=-0.2x+120多了“常数项120”
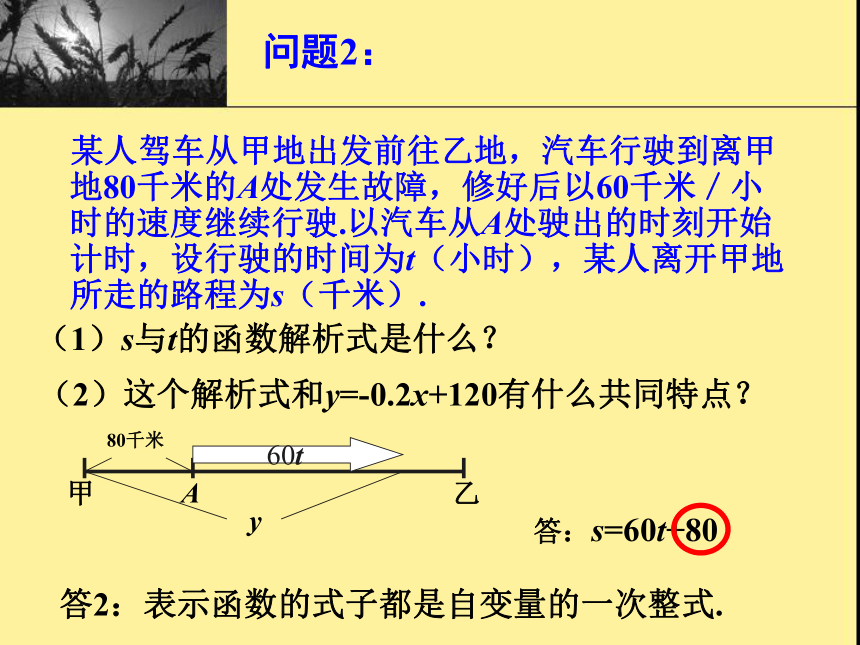
某人驾车从甲地出发前往乙地,汽车行驶到离甲地80千米的A处发生故障,修好后以60千米/小时的速度继续行驶.以汽车从A处驶出的时刻开始计时,设行驶的时间为t(小时),某人离开甲地所走的路程为s(千米).
(1)s与t的函数解析式是什么?
60t答:s=60t+80(2)这个解析式和y=-0.2x+120有什么共同特点?答2:表示函数的式子都是自变量的一次整式. 问题2:一次函数定义 一般地,解析式形如y=kx+b(k、b是常数,且k≠0)的函数叫做一次函数.
一次函数y=kx+b的定义域是一切实数.
问:一次函数与正比例函数有什么关系?思考:当b=0时, y=kx+b是什么函数?x的定义域是什么?所以正比例函数是一次函数的特例.这时y是x的正比例函数.由此可得:例题1:根据变量x、y的关系式,判断y是否是x的一次函数,如果是一次函数,请指出k、b的值.
(1)答:因为y是x的正比例函数,正比例函数是一次函数的特例,所以是的一次函数.k=2、b=0.三、例题讲解三、例题讲解例题1:根据变量x、y的关系式,判断y是否是x的一次函数,如果是一次函数,请指出k、b的值.
适时小结如何根据变量x、y的关系式, 判断y是否是x的一次函数:1、自变量x在分子上;2、自变量x的指数为1.
1、(口答)下列函数中,哪些是一次函数?课堂练习
课本第3页,练习20.1 / 1.(4)y=kx+b(k、b是常数).不是; 是 ;不是; 不是.k ≠0?例题2 已知变量x、y之间的关系式是 y=(a+1)x+a (其中a是常数),那么y是x的一次函数吗?答: 当a+1≠0,即a≠-1时,k是什么?(a+1)x+a是关于x的一次整式,这时y是x的一次函数;当a=-1时,得y=-1, 这时y不是x的一次函数.本题体现了什么数学思想?例题2 已知变量x、y之间的关系式是y=(a+1)x+a (其中a是常数),那么y是x的一次函数吗?答: 当a+1≠0,即a≠-1时,(a+1)x+a是关于x的一次整式,这时y是x的一次函数;当a=-1时,得 y=-1, 这时y不是x的一次函数.这时y是什么函数呢? 一般地,我们把函数y=c(c是常数)叫做常值函数.它的自变量由所讨论的问题决定.三、一次函数的运用例题3 已知一个一次函数,当自变量x=2时,
函数值y=-1;当x=5时,y=8.
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).用什么方法求这个函数解析式?正比例函数是用什么方法的?待定系数法三、一次函数的运用例题3 已知一个一次函数,当自变量x=2时,
函数值y=-1;当x=5时,y=8.
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).解:(1)设所求一次函数的解析式为 ;y=kx+b(k≠0)由x=2时y=-1,得 -1=2k+b; 由x=5时y= 8,得 8=5k+b; 解二元一次方程组现在已经把一次函数转化为关于k、b的二元一次方程组,解这个二元一次方程组,可以得到k、b的值. 三、一次函数的运用例题3 已知一个一次函数,当自变量x=2时,
函数值y=-1;当x=5时,y=8.
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).解:(1)设所求一次函数的解析式为 ;y=kx+b(k≠0)由x=2时y=-1,得 -1=2k+b; 由x=5时y= 8,得 8=5k+b; 解二元一次方程组得 所以,这个一次函数的解析式是 课堂练习:
课本第3页,练习20.1 / 2、32、已知一次函数
(1)求 f (-1), f (2);
(2)如果f(a)=4,求实数a的值.解:(1)解得 a=12.3、已知一个一次函数,当自变量x=-3时,函数值y=11;当x=5时,y=-5,求这个函数的解析式.
解:设所求一次函数的解析式为y=kx+b(k≠0);由x=-3时y=11,得 11=-3k+b ;由x=5时y=-5,得 -5=5k+b .解二元一次方程组得 所以,这个一次函数的解析式是y=-2x+5 .四、课堂小结 通过本节课的学习你得到了哪些新知识,又有哪些收获?1、一次函数的概念
(1)解析式“形如”y=kx+b(k、b是常数,且k≠0)
(2)定义域是一切实数.3、待定系数法求一次函数解析式. 五、布置作业: 练习册习题20.1
第 二、四象限.是不是所有的直线都经过原点呢?oy=kx(k≠0)是正比例函数图像吗?这节课就开始研究这类函数.那是什么函数图像呢?二、概念研究问题1:
汽车油箱里原有汽油120升,已知每行驶10千米耗油2升,如果汽车油箱的剩余油量是y(升)汽车行驶的路程为x(千米). (1)试用解析式表示y与x的关系. 等量关系式?剩余油量=120(升)-用去的油量答:y=120-0.2x .x的定义域是什么?每行驶10千米耗油2升,就是每千米0.2升,那么120升汽油最远可以行驶多少千米? (0≤x ≤600)二、概念研究问题1:
汽车油箱里原有汽油120升,已知每行驶10千米耗油2升,如果汽车油箱的剩余是y(升)汽车行驶的路程为x(千米). (1)试用解析式表示y与x的关系. 答:y=120-0.2x (2)这个函数与正比例函数有何不同?答:y=-0.2x+120多了“常数项120”
某人驾车从甲地出发前往乙地,汽车行驶到离甲地80千米的A处发生故障,修好后以60千米/小时的速度继续行驶.以汽车从A处驶出的时刻开始计时,设行驶的时间为t(小时),某人离开甲地所走的路程为s(千米).
(1)s与t的函数解析式是什么?
60t答:s=60t+80(2)这个解析式和y=-0.2x+120有什么共同特点?答2:表示函数的式子都是自变量的一次整式. 问题2:一次函数定义 一般地,解析式形如y=kx+b(k、b是常数,且k≠0)的函数叫做一次函数.
一次函数y=kx+b的定义域是一切实数.
问:一次函数与正比例函数有什么关系?思考:当b=0时, y=kx+b是什么函数?x的定义域是什么?所以正比例函数是一次函数的特例.这时y是x的正比例函数.由此可得:例题1:根据变量x、y的关系式,判断y是否是x的一次函数,如果是一次函数,请指出k、b的值.
(1)答:因为y是x的正比例函数,正比例函数是一次函数的特例,所以是的一次函数.k=2、b=0.三、例题讲解三、例题讲解例题1:根据变量x、y的关系式,判断y是否是x的一次函数,如果是一次函数,请指出k、b的值.
适时小结如何根据变量x、y的关系式, 判断y是否是x的一次函数:1、自变量x在分子上;2、自变量x的指数为1.
1、(口答)下列函数中,哪些是一次函数?课堂练习
课本第3页,练习20.1 / 1.(4)y=kx+b(k、b是常数).不是; 是 ;不是; 不是.k ≠0?例题2 已知变量x、y之间的关系式是 y=(a+1)x+a (其中a是常数),那么y是x的一次函数吗?答: 当a+1≠0,即a≠-1时,k是什么?(a+1)x+a是关于x的一次整式,这时y是x的一次函数;当a=-1时,得y=-1, 这时y不是x的一次函数.本题体现了什么数学思想?例题2 已知变量x、y之间的关系式是y=(a+1)x+a (其中a是常数),那么y是x的一次函数吗?答: 当a+1≠0,即a≠-1时,(a+1)x+a是关于x的一次整式,这时y是x的一次函数;当a=-1时,得 y=-1, 这时y不是x的一次函数.这时y是什么函数呢? 一般地,我们把函数y=c(c是常数)叫做常值函数.它的自变量由所讨论的问题决定.三、一次函数的运用例题3 已知一个一次函数,当自变量x=2时,
函数值y=-1;当x=5时,y=8.
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).用什么方法求这个函数解析式?正比例函数是用什么方法的?待定系数法三、一次函数的运用例题3 已知一个一次函数,当自变量x=2时,
函数值y=-1;当x=5时,y=8.
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).解:(1)设所求一次函数的解析式为 ;y=kx+b(k≠0)由x=2时y=-1,得 -1=2k+b; 由x=5时y= 8,得 8=5k+b; 解二元一次方程组现在已经把一次函数转化为关于k、b的二元一次方程组,解这个二元一次方程组,可以得到k、b的值. 三、一次函数的运用例题3 已知一个一次函数,当自变量x=2时,
函数值y=-1;当x=5时,y=8.
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).解:(1)设所求一次函数的解析式为 ;y=kx+b(k≠0)由x=2时y=-1,得 -1=2k+b; 由x=5时y= 8,得 8=5k+b; 解二元一次方程组得 所以,这个一次函数的解析式是 课堂练习:
课本第3页,练习20.1 / 2、32、已知一次函数
(1)求 f (-1), f (2);
(2)如果f(a)=4,求实数a的值.解:(1)解得 a=12.3、已知一个一次函数,当自变量x=-3时,函数值y=11;当x=5时,y=-5,求这个函数的解析式.
解:设所求一次函数的解析式为y=kx+b(k≠0);由x=-3时y=11,得 11=-3k+b ;由x=5时y=-5,得 -5=5k+b .解二元一次方程组得 所以,这个一次函数的解析式是y=-2x+5 .四、课堂小结 通过本节课的学习你得到了哪些新知识,又有哪些收获?1、一次函数的概念
(1)解析式“形如”y=kx+b(k、b是常数,且k≠0)
(2)定义域是一切实数.3、待定系数法求一次函数解析式. 五、布置作业: 练习册习题20.1
