20.2 一次函数的图像 课件(16张PPT)
文档属性
| 名称 | 20.2 一次函数的图像 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 299.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览




文档简介
课件16张PPT。20.2 一次函数的图像 复习引入画一次函数图像的步骤是什么?一“读”二“算”三“画” 复习引入问:下列直线与y轴的交点是什么? 答:四条直线与y轴的交点都是(0,2)你能得到什么结论? 这四条直线都经过同一点(0,2)b 的作用 学习新知 在坐标平面上截距b相同的直线
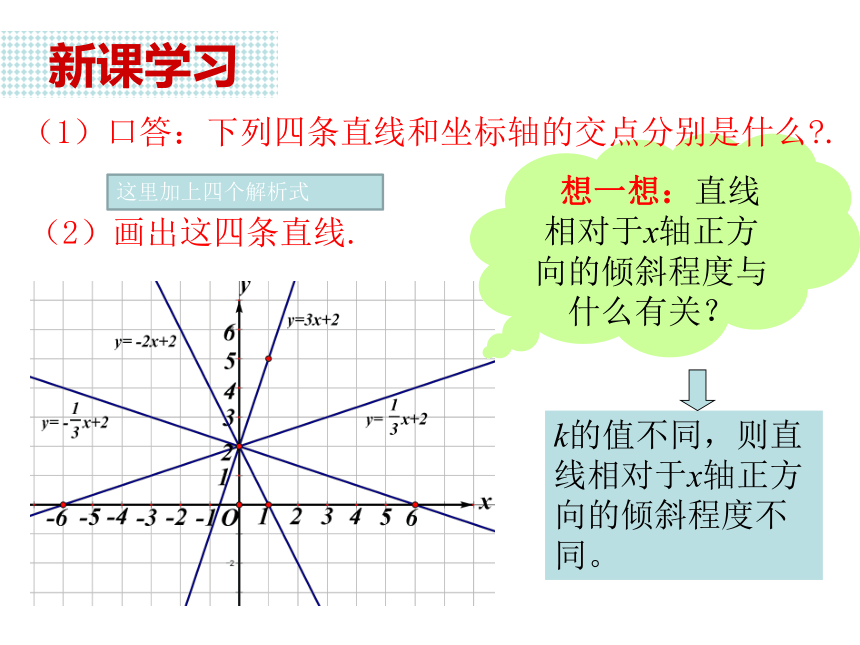
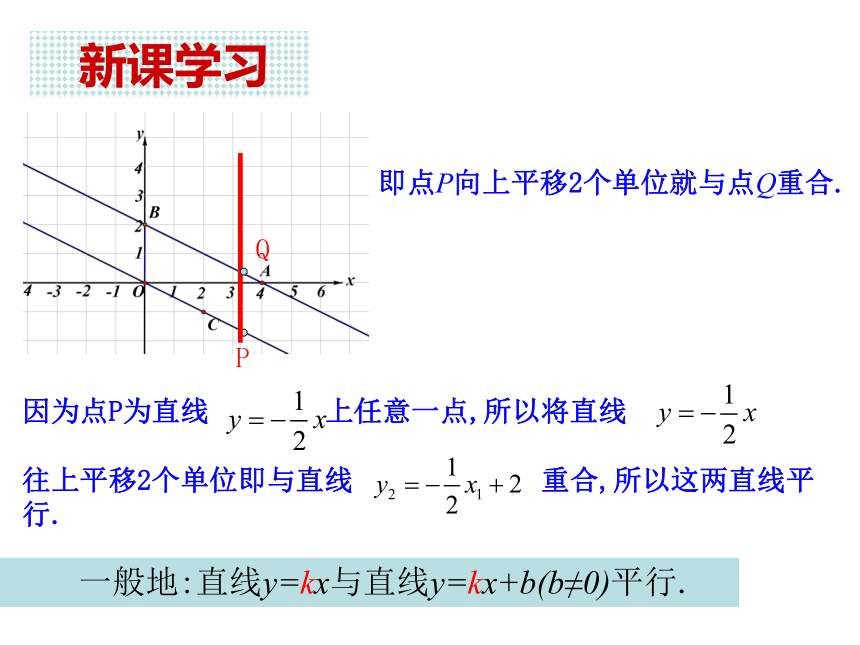
经过同一点(0,b).y=kx+b (k≠0)y=kx+b (k≠0) 新课学习 想一想:直线相对于x轴正方向的倾斜程度与什么有关? (1)口答:下列四条直线和坐标轴的交点分别是什么?.(2)画出这四条直线.这里加上四个解析式 新课学习如何判断这两条直线之间的位置关系?点O向上平移两个单位就与点B重合。分析: 新课学习即点P向上平移2个单位就与点Q重合.因为点P为直线 上任意一点,所以将直线
往上平移2个单位即与直线 重合,所以这两直线平行. 一般地:直线y=kx与直线y=kx+b(b≠0)平行.1. 两个函数图像的关系 结论2. 直线平行 及时练习1.指出下列直线中互相平行的直线:如何判断两条直线平行?解:(1)和(4)平行; (2)和(6)平行;
(3)和(5)平行。 知识运用例2 已知一次函数的图像经过点A(2,-1),且与直线y= x+1平行.(1)求这个函数的解析式.设一次函数解析为 y=kx+b(k≠0),如何确定k、b的值?解:设一次函数解析式为y=kx+b(k≠0). 如何求b? 知识运用例5 已知一次函数的图像经过点A(2,-1),且与直线y= x+1平行.(2)求这条直线与坐标轴围成的图形面积 . 如何求面积? 即这条直线与坐标轴围成的图形
面积为4 . 小结:确定直线与坐标轴围成的三角形面积:读、算、代入三角形面积公式(坐标加绝对值). 巩固练习2. 已知直线y=(m-1)x+m与直线y=2x+1平行.(1)求m的值;解得 m=3.(2)求直线y=(m-1)x+m与x轴的交点坐标;把m=3代入解析式,得 y=2x+3.令y=0,得0=2x+3,
巩固练习3. 已知一次函数的图像经过点M(-3,2),且平行于直线y=4x-1.解:设一次函数解析式为y=kx+b(k≠0).(1)求这个函数的解析式;(2)求这个函数图像与坐标轴围成的三角形的面积;解:直线y= 4x+14与y轴的交点C (0,14); 令y=0,得4x+14=0,解得x= . 直线y=4x+14与x轴的交点B( ,0). 课堂小结这节课你有什么收获和体会?2.如何确定直线与坐标轴围成的三角形面积?读、算、代入三角形面积公式(坐标加绝对值). 布置作业《练习册》 习题 20.2(2)
经过同一点(0,b).y=kx+b (k≠0)y=kx+b (k≠0) 新课学习 想一想:直线相对于x轴正方向的倾斜程度与什么有关? (1)口答:下列四条直线和坐标轴的交点分别是什么?.(2)画出这四条直线.这里加上四个解析式 新课学习如何判断这两条直线之间的位置关系?点O向上平移两个单位就与点B重合。分析: 新课学习即点P向上平移2个单位就与点Q重合.因为点P为直线 上任意一点,所以将直线
往上平移2个单位即与直线 重合,所以这两直线平行. 一般地:直线y=kx与直线y=kx+b(b≠0)平行.1. 两个函数图像的关系 结论2. 直线平行 及时练习1.指出下列直线中互相平行的直线:如何判断两条直线平行?解:(1)和(4)平行; (2)和(6)平行;
(3)和(5)平行。 知识运用例2 已知一次函数的图像经过点A(2,-1),且与直线y= x+1平行.(1)求这个函数的解析式.设一次函数解析为 y=kx+b(k≠0),如何确定k、b的值?解:设一次函数解析式为y=kx+b(k≠0). 如何求b? 知识运用例5 已知一次函数的图像经过点A(2,-1),且与直线y= x+1平行.(2)求这条直线与坐标轴围成的图形面积 . 如何求面积? 即这条直线与坐标轴围成的图形
面积为4 . 小结:确定直线与坐标轴围成的三角形面积:读、算、代入三角形面积公式(坐标加绝对值). 巩固练习2. 已知直线y=(m-1)x+m与直线y=2x+1平行.(1)求m的值;解得 m=3.(2)求直线y=(m-1)x+m与x轴的交点坐标;把m=3代入解析式,得 y=2x+3.令y=0,得0=2x+3,
巩固练习3. 已知一次函数的图像经过点M(-3,2),且平行于直线y=4x-1.解:设一次函数解析式为y=kx+b(k≠0).(1)求这个函数的解析式;(2)求这个函数图像与坐标轴围成的三角形的面积;解:直线y= 4x+14与y轴的交点C (0,14); 令y=0,得4x+14=0,解得x= . 直线y=4x+14与x轴的交点B( ,0). 课堂小结这节课你有什么收获和体会?2.如何确定直线与坐标轴围成的三角形面积?读、算、代入三角形面积公式(坐标加绝对值). 布置作业《练习册》 习题 20.2(2)
