一次函数中的错解剖析 课件(20张PPT)
文档属性
| 名称 | 一次函数中的错解剖析 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览








文档简介
课件20张PPT。一次函数中的错解剖析●定义运用不当所导致的错解
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
例1:已知函数y=4x+m-2,
(1)m为何值时,y是x的正比例函数?
(2)m为何值时,y是x的一次函数?
火眼金睛形如y=kx(k为常数,且k≠0)形如y=kx+b(k、b为常数,且k≠0)正比例函数是一次函数的特例正确(2)m无论取任何实数时, y都是x的一次函数。42%例2:若函数y=mx+(x+1) 是一次函数,则
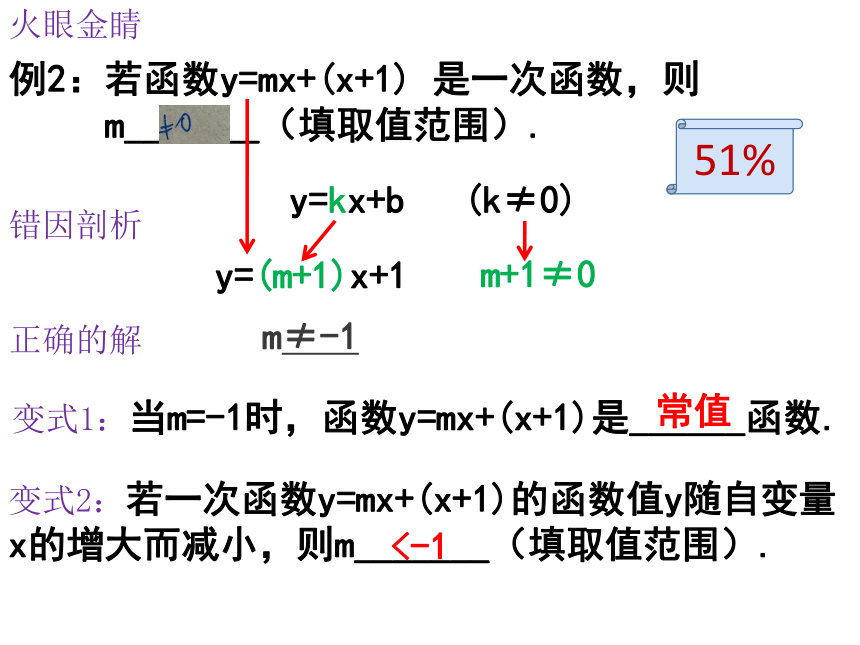
m_______(填取值范围).火眼金睛错因剖析y=kx+b (k≠0)y=(m+1)x+1 正确的解m≠-1m+1≠0变式2:若一次函数y=mx+(x+1)的函数值y随自变量x的增大而减小,则m_______(填取值范围).<-1变式1:当m=-1时,函数y=mx+(x+1)是______函数.常值51%忽视y=kx+b中k≠0的要求
火眼金睛错因剖析例3:已知函数
是一次函数,求m的取值范围.错解42%练习一1、函数y=(m+1)x+ m-1必定是一次函数吗?
为什么?2、m为何值时,函数y=(m+1)xm2+ m-1是一次函数?
此时它是正比例函数吗?不一定.当m ≠-1时,此函数为一次函数;当m =-1时,此函数为常值函数y=-2.解:由m+1 ≠0m2=1解得 m=1.此时,函数解析式为y=2x,是正比例函数。解:●定义运用不当所导致的错解
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
例4:如果直线 y=x+m 不经过第二象限,
那么实数m的取值范围是什么?
火眼金睛正比例函数是一次函数的特例错因剖析正确的解错解m≤0变式:直线 y=x+m 还有可能不经过第______象限,
此时m的取值范围是______.四m≥047%没有数形结合例5:已知一次函数y=(2k+1)x+1-2k的图像在第一、三、四象限,则k的取值范围为_______.
火眼金睛 (选自本次期中考试)计算不准确错因剖析正确的解错解没有注意数形结合解:由2k+1 >01-2k<0解得 30%1、直线y=kx+b(k≠0)经过第一、二、四象限,则
K 0, b 0 .(填<、>、≤或≥) <>此时,直线y=bx+k的图像只能是( ) D练习二2、一次函数y=(1-2k)x+2-k (k≠0)不经过第三象
限,则k的取值范围是 .2-k ≥ 01-2k<0≤2●定义运用不当所导致的错解
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
例6:若一次函数y=kx+2与两坐标轴围成的三角形面积是4,求k的值.
火眼金睛错解(0,2)ABB’
65%练习三1、已知一次函数y=kx+b(k≠0)的图像经过点A(4,0),且与两坐标轴所围成的三角形的面积为6,求此函数的解析式.(4,0)(0,3)(0,-3)ABB’●定义运用不当所导致的错解
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
火眼金睛正确的解例7:小红骑自行车到离家为2千米的书店买书,行驶了5分钟后,遇到一个同学因说话停留10分钟,继续骑了5分钟到书店.
下列哪个图象能大致描述她去书店过程中离书店的距离S(千米)与所用时间t(分)之间的关系( ).
D71%“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟先到达终点P。用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事相吻合的是( )D练习四请你根据图表,充分发挥你的想象,自编一则新的“龟兔赛跑”的寓言故事,要求如下:
(1)用简洁明快的语言概括大意;
(2)图表中能确定的数值,在故事叙述中不得少于3个,且要分别涉及时间、路程和速度这三个量。新龟兔赛跑谢谢!兔龟40300谢谢!
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
例1:已知函数y=4x+m-2,
(1)m为何值时,y是x的正比例函数?
(2)m为何值时,y是x的一次函数?
火眼金睛形如y=kx(k为常数,且k≠0)形如y=kx+b(k、b为常数,且k≠0)正比例函数是一次函数的特例正确(2)m无论取任何实数时, y都是x的一次函数。42%例2:若函数y=mx+(x+1) 是一次函数,则
m_______(填取值范围).火眼金睛错因剖析y=kx+b (k≠0)y=(m+1)x+1 正确的解m≠-1m+1≠0变式2:若一次函数y=mx+(x+1)的函数值y随自变量x的增大而减小,则m_______(填取值范围).<-1变式1:当m=-1时,函数y=mx+(x+1)是______函数.常值51%忽视y=kx+b中k≠0的要求
火眼金睛错因剖析例3:已知函数
是一次函数,求m的取值范围.错解42%练习一1、函数y=(m+1)x+ m-1必定是一次函数吗?
为什么?2、m为何值时,函数y=(m+1)xm2+ m-1是一次函数?
此时它是正比例函数吗?不一定.当m ≠-1时,此函数为一次函数;当m =-1时,此函数为常值函数y=-2.解:由m+1 ≠0m2=1解得 m=1.此时,函数解析式为y=2x,是正比例函数。解:●定义运用不当所导致的错解
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
例4:如果直线 y=x+m 不经过第二象限,
那么实数m的取值范围是什么?
火眼金睛正比例函数是一次函数的特例错因剖析正确的解错解m≤0变式:直线 y=x+m 还有可能不经过第______象限,
此时m的取值范围是______.四m≥047%没有数形结合例5:已知一次函数y=(2k+1)x+1-2k的图像在第一、三、四象限,则k的取值范围为_______.
火眼金睛 (选自本次期中考试)计算不准确错因剖析正确的解错解没有注意数形结合解:由2k+1 >01-2k<0解得 30%1、直线y=kx+b(k≠0)经过第一、二、四象限,则
K 0, b 0 .(填<、>、≤或≥) <>此时,直线y=bx+k的图像只能是( ) D练习二2、一次函数y=(1-2k)x+2-k (k≠0)不经过第三象
限,则k的取值范围是 .2-k ≥ 01-2k<0≤2●定义运用不当所导致的错解
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
例6:若一次函数y=kx+2与两坐标轴围成的三角形面积是4,求k的值.
火眼金睛错解(0,2)ABB’
65%练习三1、已知一次函数y=kx+b(k≠0)的图像经过点A(4,0),且与两坐标轴所围成的三角形的面积为6,求此函数的解析式.(4,0)(0,3)(0,-3)ABB’●定义运用不当所导致的错解
●性质、图像运用中的错解
●一次函数与坐标轴围成的三角形面积问题中的错解
●与实际问题有关的图像题中的错解
火眼金睛正确的解例7:小红骑自行车到离家为2千米的书店买书,行驶了5分钟后,遇到一个同学因说话停留10分钟,继续骑了5分钟到书店.
下列哪个图象能大致描述她去书店过程中离书店的距离S(千米)与所用时间t(分)之间的关系( ).
D71%“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟先到达终点P。用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事相吻合的是( )D练习四请你根据图表,充分发挥你的想象,自编一则新的“龟兔赛跑”的寓言故事,要求如下:
(1)用简洁明快的语言概括大意;
(2)图表中能确定的数值,在故事叙述中不得少于3个,且要分别涉及时间、路程和速度这三个量。新龟兔赛跑谢谢!兔龟40300谢谢!
