20.4 一次函数的应用 课件(11张PPT)
文档属性
| 名称 | 20.4 一次函数的应用 课件(11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览




文档简介
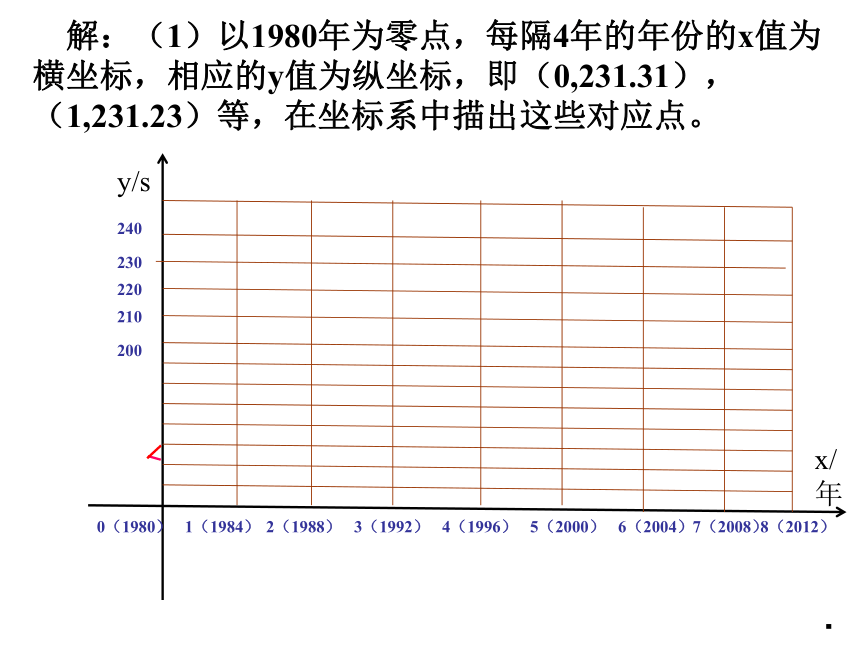
课件11张PPT。一次函数的应用 (问题①) 奥运会每4年举办一次,奥运会的游泳成绩在不断的被刷新,如男子400m自由泳项目,1996年奥运冠军的成绩比1960年的约提高了30s,下面是该项目冠军的一些数据:根据上面资料,能否估计2012年伦敦奥运会时该项目的冠军成绩? 解:(1)以1980年为零点,每隔4年的年份的x值为横坐标,相应的y值为纵坐标,即(0,231.31),(1,231.23)等,在坐标系中描出这些对应点。· 确定一次函数关系式,关键是选出两个点的坐标,选哪两个点呢?(参看课本P58页的边注。)(2)观察描出的点的整体分布,他们基本在一条直线附近波动,y与x之间的函数 关系可以用一次函数去模拟。即:y=kx+b········ 这里我们选取从原点向右的第1个点(1,231.23)及第7个点(7,221.86)的坐标代入y=kx+b中,得解方程组可得:k=-1.63, b=232.86所以,一次函数的解析式为:y=-1.63x+232.863. 当把1980年的x值作为0,以后每增加4年得x的一个值,这样2012年时的x值为8,把x=8代入上式,得y=-1.63×8+232.86=219.82(s)因此,可以得到2012年奥运会男子的自由泳的400m的冠军的成绩约是219.82s 2012年伦敦奥运会中国选手孙杨以220.14s的成绩打破男子400m自由泳项目奥运会纪录获得冠军,你对你预测的准确程度满意吗?(4)能否用上述模型预测2016年里约热内卢奥运会该项目的冠军成绩?通过上面的学习,我们可以知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:(1)将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题。问题② 球从高处下落再反弹起来,可以直观的看出球的下落高度越高,反弹高度也越高,那么球下落高度与反弹高度具有怎样的关系呢?请你进行试验,将试验数据填入下表,并根据试验数据建立球下落高度和反弹高度之间关系的函数模型。课堂小结:写出函数关系式,建立实际问题的数学模型
作业: 请你选择一个可以应用函数模型解决的问题,并建立合适的函数模型。
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题。问题② 球从高处下落再反弹起来,可以直观的看出球的下落高度越高,反弹高度也越高,那么球下落高度与反弹高度具有怎样的关系呢?请你进行试验,将试验数据填入下表,并根据试验数据建立球下落高度和反弹高度之间关系的函数模型。课堂小结:写出函数关系式,建立实际问题的数学模型
作业: 请你选择一个可以应用函数模型解决的问题,并建立合适的函数模型。
