沪教版八年级数学下册 22.1多边形的内角和 课件(15张PPT)
文档属性
| 名称 | 沪教版八年级数学下册 22.1多边形的内角和 课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 408.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-27 00:00:00 | ||
图片预览




文档简介
课件15张PPT。22.1 (1)多边形的内角和类比三角形学习多边形相关概念 三角形是由不在同一直线上的_______ 条线段 联结所组成的封闭图形.三首尾顺次 多边形是由不在同一直线上的_______ 线段 联结所组成的封闭图形.一些首尾顺次 相邻两条线段的公共端点叫做________________类比三角形学习多边形相关概念 组成多边形的每一条线段叫做 ______________ 多边形相邻两边所成的角叫做
________________多边形的内角多边形的边多边形的顶点 组成三角形的每一条线段叫做三角形的边 相邻两条线段的公共端点叫做 三角形的顶点 三角形相邻两边所成的角叫做 三角形的内角ABCDE记做 五边形ABCDEn边形有 _____条边,_______个顶点,________个内角nnn一个多边形,如果画出它的任意一条边所在的直线,
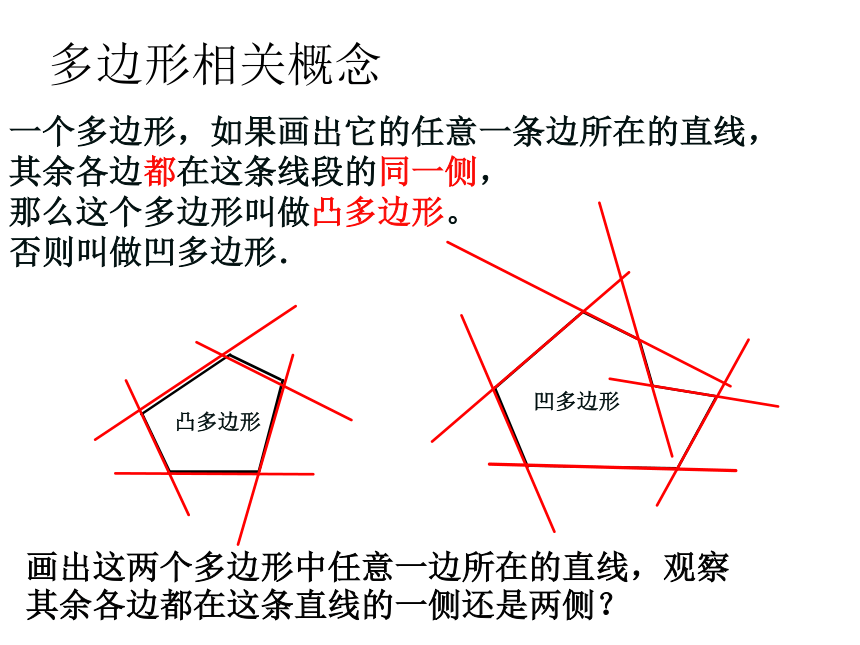
其余各边都在这条线段的同一侧,
那么这个多边形叫做凸多边形。
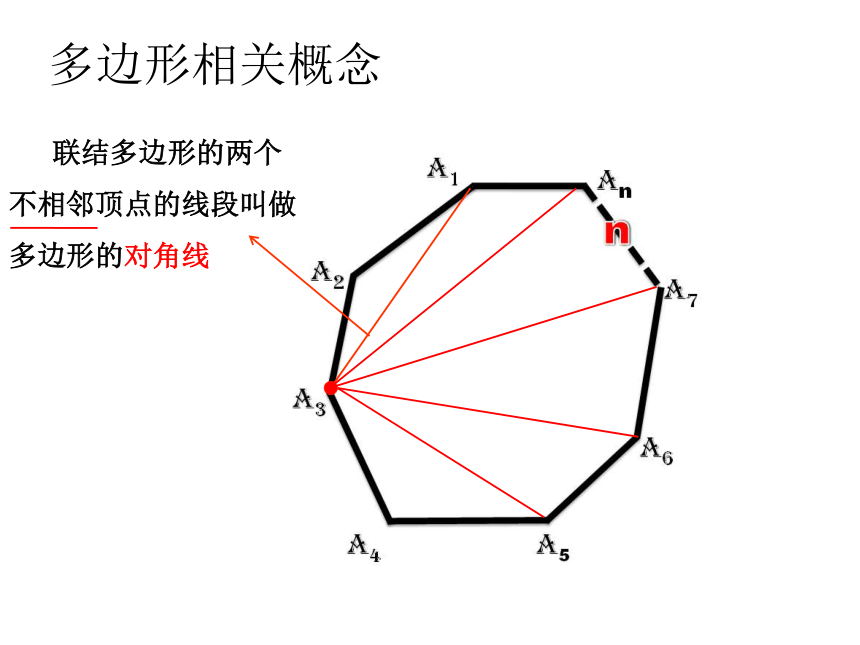
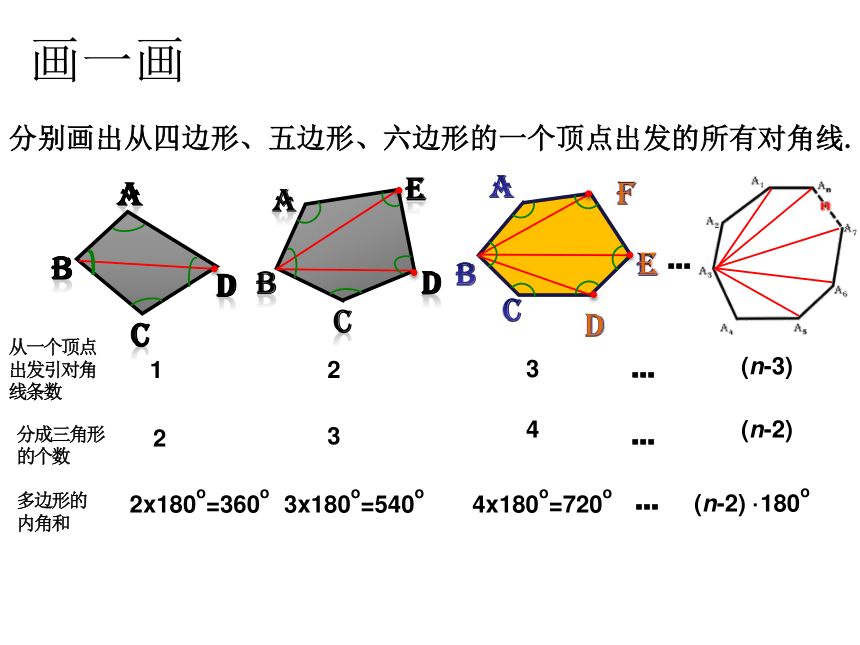
否则叫做凹多边形.凹多边形凸多边形多边形相关概念画出这两个多边形中任意一边所在的直线,观察其余各边都在这条直线的一侧还是两侧?多边形相关概念 联结多边形的两个不相邻顶点的线段叫做多边形的对角线画一画分别画出从四边形、五边形、六边形的一个顶点出发的所有对角线.123(n-3)234(n-2)2x180o=360o3x180o=540o4x180o=720o(n-2) ·180oDDEDEF从一个顶点出发引对角线条数多边形的
内角和分成三角形的个数…………归纳总结多边形的内角和定理多边形的内角和定理:n边形的内角和等于(n-2) · 180o
(n ≥ 3的整数)合作,探究问题:
你还有其他的方法推导出多边形的内角和吗?请以四边形为例说明.应用新知,尝试练习
例题讲解一:
例1. 求十边形的内角和. 例2. 已知一个多边形的内角和是2160o,
求它的边数.1.填一填:
①n+1边形的内角和比n边形的内角和大______度.
②一个多边形的内角和不可能是( )
1080o B. 360o C.1000o D. 900o
③在四边形ABCD中, ∠ A=120o ,∠B: ∠C: ∠D=3:4:5
则∠B= _____度
④如图DF是边CD的延长线,
则图中x=_____度.
⑤一个多边形的内角和是1800o ,它是 边形。
应用新知,尝试练习
18045C十二60例题讲解二:
例3. 一个多边形的各个内角都是
120°,求它的边数。应用新知,尝试练习
1. 一个多边形的各个内角都是90°,则它是 ____边形。四应用新知,尝试练习
2、每个内角等于144°的多边形是_______边形;十归纳总结,形成体系本节课你学习到了什么知识?多边形的内角和定理
n边形的内角和等于(n-2) · 180o(n ≥3的整数)
几个概念:
多边形的定义、多边形的边、内角、顶点、对角线、凸多边形、凹多边形布置作业1、练习册:22.1(1)2、思考
将一个多边形截去一个角,所得多边形的内角和是,那么这个多边形原来是几边形?
. 谢 谢!
________________多边形的内角多边形的边多边形的顶点 组成三角形的每一条线段叫做三角形的边 相邻两条线段的公共端点叫做 三角形的顶点 三角形相邻两边所成的角叫做 三角形的内角ABCDE记做 五边形ABCDEn边形有 _____条边,_______个顶点,________个内角nnn一个多边形,如果画出它的任意一条边所在的直线,
其余各边都在这条线段的同一侧,
那么这个多边形叫做凸多边形。
否则叫做凹多边形.凹多边形凸多边形多边形相关概念画出这两个多边形中任意一边所在的直线,观察其余各边都在这条直线的一侧还是两侧?多边形相关概念 联结多边形的两个不相邻顶点的线段叫做多边形的对角线画一画分别画出从四边形、五边形、六边形的一个顶点出发的所有对角线.123(n-3)234(n-2)2x180o=360o3x180o=540o4x180o=720o(n-2) ·180oDDEDEF从一个顶点出发引对角线条数多边形的
内角和分成三角形的个数…………归纳总结多边形的内角和定理多边形的内角和定理:n边形的内角和等于(n-2) · 180o
(n ≥ 3的整数)合作,探究问题:
你还有其他的方法推导出多边形的内角和吗?请以四边形为例说明.应用新知,尝试练习
例题讲解一:
例1. 求十边形的内角和. 例2. 已知一个多边形的内角和是2160o,
求它的边数.1.填一填:
①n+1边形的内角和比n边形的内角和大______度.
②一个多边形的内角和不可能是( )
1080o B. 360o C.1000o D. 900o
③在四边形ABCD中, ∠ A=120o ,∠B: ∠C: ∠D=3:4:5
则∠B= _____度
④如图DF是边CD的延长线,
则图中x=_____度.
⑤一个多边形的内角和是1800o ,它是 边形。
应用新知,尝试练习
18045C十二60例题讲解二:
例3. 一个多边形的各个内角都是
120°,求它的边数。应用新知,尝试练习
1. 一个多边形的各个内角都是90°,则它是 ____边形。四应用新知,尝试练习
2、每个内角等于144°的多边形是_______边形;十归纳总结,形成体系本节课你学习到了什么知识?多边形的内角和定理
n边形的内角和等于(n-2) · 180o(n ≥3的整数)
几个概念:
多边形的定义、多边形的边、内角、顶点、对角线、凸多边形、凹多边形布置作业1、练习册:22.1(1)2、思考
将一个多边形截去一个角,所得多边形的内角和是,那么这个多边形原来是几边形?
. 谢 谢!
