沪教版八年级数学下册 22.1 多边形的外角和课件(第2课时 21张PPT)
文档属性
| 名称 | 沪教版八年级数学下册 22.1 多边形的外角和课件(第2课时 21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 979.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-27 00:00:00 | ||
图片预览







文档简介
课件21张PPT。练习
1.九边形的内角和等于 度;
2.一个多边形的内角和等于1440o,这个多边形是 边形. 多边形内角和定理
n边形的内角和等于 .
(n–2)·180o (n–2)?180o1260 1260 1260 1260 1260 1260十清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步.(1)小明每从一条小路转到下一条小路时,他所转过的角是哪个角?
(2)他每跑完一圈,他转过的角度之和是多少?
∠1+∠2+ ∠3+ ∠4+∠5
=
∠1、∠2、∠3、∠4、∠5
A BCDE15432多边形的一个内角的邻补角叫做多边形的外角.这个角是内角的什么角?6同一个内角相邻的外角有几个?它们有什么关系?内角 A BCDE15432∠1+∠2+∠3+∠4+∠5=?
对多边形的每一个内角,从与它相邻的两个外角中取一个,这样取得的所有外角的和,叫做多边形的外角和.求五边形的外角和求五边形的外角和 A BCDE15432
五边形外角和= 360 °= 五个平角-五边形内角和 = 5×180°-(5-2) × 180°∠1+∠6=?
∠2+∠7=?
∠3+∠8=?
∠4+∠9=?
∠5+∠10=?
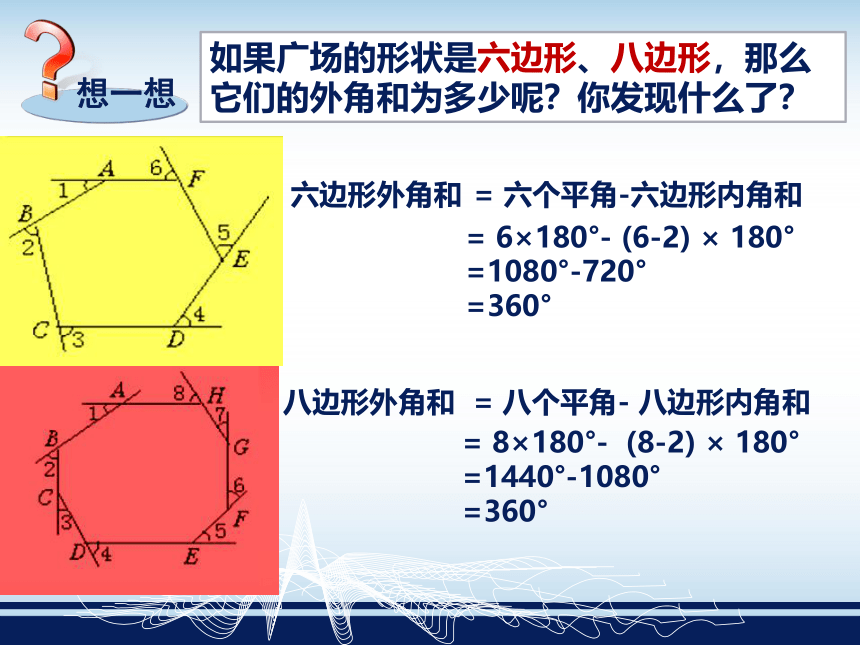
∠6+∠7+∠8+∠9+∠10=?=180°∠1+∠2+∠3+∠4+∠5=?679108如果广场的形状是六边形、八边形,那么它们的外角和为多少呢?你发现什么了?六边形外角和= 六个平角-六边形内角和 = 6×180°- (6-2) × 180°
=1080°-720°
=360°八边形外角和= 八个平角- 八边形内角和 = 8×180°- (8-2) × 180°
=1440°-1080°
=360°
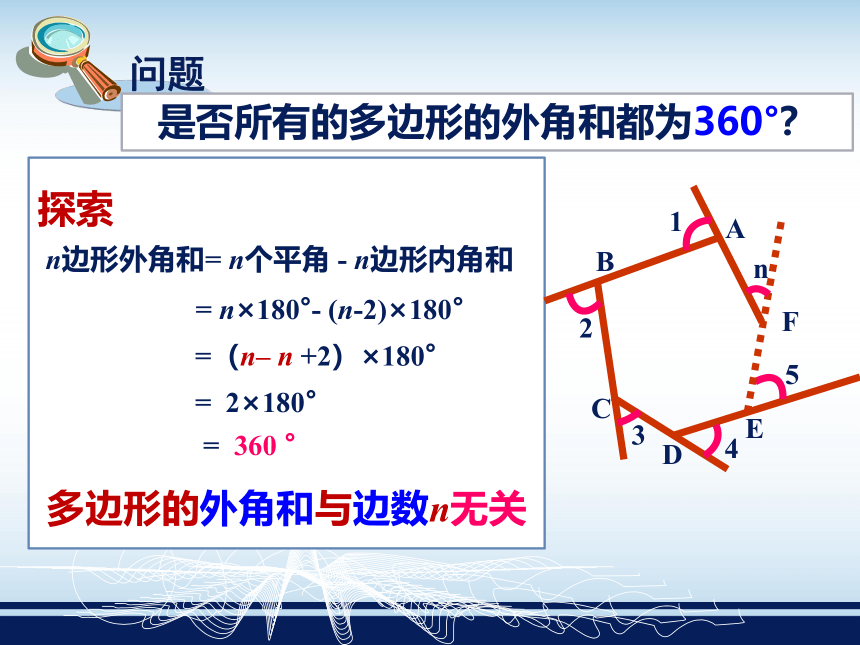
探索
n边形外角和= n个平角 - n边形内角和
= 360 °= n×180°- (n-2)×180°是否所有的多边形的外角和都为360°?=(n– n +2)×180°= 2×180°多边形的外角和与边数n无关多边形的外角和等于360°.注意:
1.多边形的内角和随着边数的增加而增加;
2.多边形的外角和为一个定值,与边数无关;
3.特殊情况:
如果多边形(边数为n)的每个外角都相等n每个外角的度数=360°.×应
用分析:解:设多边形的边数为n,根据题意,得 n·72o= 360o.解得n=5.例题4 一个多边形的每个外角都是72 o,这个多边形是几边形?还有别的方法吗?答:这个多边形是五边形.n每个外角的度数×=360°.应
用分析:
∠A + ∠2+ ∠B +∠D=360o例题5 如图,∠BCE是四边形ABCD的一个外角,如果∠BCE=∠A,求∠B+∠D的度数. ∠A+∠2=180o∠1+∠2=180o ∠1=∠A整体的思想应
用解:∵∠1+∠2=180o,∠1=∠A,
∴∠A+∠2=180o.例题5 如图,∠BCE是四边形ABCD的一个外角,如果∠BCE=∠A,求∠B+∠D的度数. 又∵∠A +∠B+∠2+∠D=360o
(四边形的内角和等于360o), ∴∠B+∠D=360o–(∠A+∠2)
=360o–180o
=180o.如果∠B与∠D互为补角,那么∠BCE与∠A的大小相等吗?应
用变式 已知:如图,∠BCE是四边形ABCD
的一个外角,∠B+∠D=180° ,
求证:∠BCE=∠A. 如果∠B与∠D互为补角,那么∠BCE与∠A的大小相等吗?分析: ∠B+∠D=180o ∠A + ∠2+ ∠B +∠D=360o ∠A+∠2=180o∠1+∠2=180o ∠1=∠A练
习分析:内角和=外角和解:设这个多边形的边数为n.
(n—2)·180o=360o.
解得 n=4.
答:这个多边形为四边形. 1.如果一个多边形的内角和与外角和相等,那么这个多边形的边数是多少?练
习分析:
1.如果多边形(边数为n)的每个外角都等于20°
由 n×20°=360°可求得n;
2.由每个外角为20°,得每个内角为160°,则
多边形的内角和=160°×n. 解:设多边形的边数为n,根据题意,得
n·20o= 360o.
解得n=18.
十八边形的每个内角=180°﹣20°=160°
十八边形的内角=18×160o=2880o.
答:这个多边形的内角和是2880o.2.如果一个多边形的每个外角都等于20o,那么这个多边形的内角和是多少度? 1.多边形中各内角不相等时,
多边形内角和=(n-2)×180°;
2.多边形中各内角都相等时,
多边形内角和= n×每个内角的度数练
习分析:由于内角和相邻的外角是互补的角,当内角是锐角时,相邻的外角就是钝角.解:在一个多边形中,它的内角中最多只有3个是锐角. 3.在一个多边形中,它的内角中最多有几个锐角?外角中最多有几个钝角? 多边形的外角和是360°,外角中最多有3个钝角.B某居民小区搞绿化,分别在四边形、六边形的广场修建如图半径为2米得草坪,小区绿化组长想先求草坪面积,再根据面积买草坪。
你能帮绿化组长求出草坪的面积么? A、B哪一个图形中的草坪面积较大?(结果保留π)
?
?
?
?
?
?
?
?
? A拓
展1如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数?
?
?
?
?
?
?
?
? 拓
展21.多边形外角的定义
多边形的一个内角的邻补角叫做多边形的外角.本节课你有哪些收获或思考?2.多边形外角和的定义
对多边形的每一个内角,从与它相邻的两个外角中取一个,这样取得的所有外角的和,叫做多边形的外角和.3.任意多边形的外角和等于360°.五边形、六边形、八边形n边形特殊一般边数改变
结论不变特殊情况:
如果多边形(边数为n)的每个外角都相等n每个外角的度数=360°.×n每个内角的度数=内角和.×练习册 22.1(2)
1.九边形的内角和等于 度;
2.一个多边形的内角和等于1440o,这个多边形是 边形. 多边形内角和定理
n边形的内角和等于 .
(n–2)·180o (n–2)?180o1260 1260 1260 1260 1260 1260十清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步.(1)小明每从一条小路转到下一条小路时,他所转过的角是哪个角?
(2)他每跑完一圈,他转过的角度之和是多少?
∠1+∠2+ ∠3+ ∠4+∠5
=
∠1、∠2、∠3、∠4、∠5
A BCDE15432多边形的一个内角的邻补角叫做多边形的外角.这个角是内角的什么角?6同一个内角相邻的外角有几个?它们有什么关系?内角 A BCDE15432∠1+∠2+∠3+∠4+∠5=?
对多边形的每一个内角,从与它相邻的两个外角中取一个,这样取得的所有外角的和,叫做多边形的外角和.求五边形的外角和求五边形的外角和 A BCDE15432
五边形外角和= 360 °= 五个平角-五边形内角和 = 5×180°-(5-2) × 180°∠1+∠6=?
∠2+∠7=?
∠3+∠8=?
∠4+∠9=?
∠5+∠10=?
∠6+∠7+∠8+∠9+∠10=?=180°∠1+∠2+∠3+∠4+∠5=?679108如果广场的形状是六边形、八边形,那么它们的外角和为多少呢?你发现什么了?六边形外角和= 六个平角-六边形内角和 = 6×180°- (6-2) × 180°
=1080°-720°
=360°八边形外角和= 八个平角- 八边形内角和 = 8×180°- (8-2) × 180°
=1440°-1080°
=360°
探索
n边形外角和= n个平角 - n边形内角和
= 360 °= n×180°- (n-2)×180°是否所有的多边形的外角和都为360°?=(n– n +2)×180°= 2×180°多边形的外角和与边数n无关多边形的外角和等于360°.注意:
1.多边形的内角和随着边数的增加而增加;
2.多边形的外角和为一个定值,与边数无关;
3.特殊情况:
如果多边形(边数为n)的每个外角都相等n每个外角的度数=360°.×应
用分析:解:设多边形的边数为n,根据题意,得 n·72o= 360o.解得n=5.例题4 一个多边形的每个外角都是72 o,这个多边形是几边形?还有别的方法吗?答:这个多边形是五边形.n每个外角的度数×=360°.应
用分析:
∠A + ∠2+ ∠B +∠D=360o例题5 如图,∠BCE是四边形ABCD的一个外角,如果∠BCE=∠A,求∠B+∠D的度数. ∠A+∠2=180o∠1+∠2=180o ∠1=∠A整体的思想应
用解:∵∠1+∠2=180o,∠1=∠A,
∴∠A+∠2=180o.例题5 如图,∠BCE是四边形ABCD的一个外角,如果∠BCE=∠A,求∠B+∠D的度数. 又∵∠A +∠B+∠2+∠D=360o
(四边形的内角和等于360o), ∴∠B+∠D=360o–(∠A+∠2)
=360o–180o
=180o.如果∠B与∠D互为补角,那么∠BCE与∠A的大小相等吗?应
用变式 已知:如图,∠BCE是四边形ABCD
的一个外角,∠B+∠D=180° ,
求证:∠BCE=∠A. 如果∠B与∠D互为补角,那么∠BCE与∠A的大小相等吗?分析: ∠B+∠D=180o ∠A + ∠2+ ∠B +∠D=360o ∠A+∠2=180o∠1+∠2=180o ∠1=∠A练
习分析:内角和=外角和解:设这个多边形的边数为n.
(n—2)·180o=360o.
解得 n=4.
答:这个多边形为四边形. 1.如果一个多边形的内角和与外角和相等,那么这个多边形的边数是多少?练
习分析:
1.如果多边形(边数为n)的每个外角都等于20°
由 n×20°=360°可求得n;
2.由每个外角为20°,得每个内角为160°,则
多边形的内角和=160°×n. 解:设多边形的边数为n,根据题意,得
n·20o= 360o.
解得n=18.
十八边形的每个内角=180°﹣20°=160°
十八边形的内角=18×160o=2880o.
答:这个多边形的内角和是2880o.2.如果一个多边形的每个外角都等于20o,那么这个多边形的内角和是多少度? 1.多边形中各内角不相等时,
多边形内角和=(n-2)×180°;
2.多边形中各内角都相等时,
多边形内角和= n×每个内角的度数练
习分析:由于内角和相邻的外角是互补的角,当内角是锐角时,相邻的外角就是钝角.解:在一个多边形中,它的内角中最多只有3个是锐角. 3.在一个多边形中,它的内角中最多有几个锐角?外角中最多有几个钝角? 多边形的外角和是360°,外角中最多有3个钝角.B某居民小区搞绿化,分别在四边形、六边形的广场修建如图半径为2米得草坪,小区绿化组长想先求草坪面积,再根据面积买草坪。
你能帮绿化组长求出草坪的面积么? A、B哪一个图形中的草坪面积较大?(结果保留π)
?
?
?
?
?
?
?
?
? A拓
展1如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数?
?
?
?
?
?
?
?
? 拓
展21.多边形外角的定义
多边形的一个内角的邻补角叫做多边形的外角.本节课你有哪些收获或思考?2.多边形外角和的定义
对多边形的每一个内角,从与它相邻的两个外角中取一个,这样取得的所有外角的和,叫做多边形的外角和.3.任意多边形的外角和等于360°.五边形、六边形、八边形n边形特殊一般边数改变
结论不变特殊情况:
如果多边形(边数为n)的每个外角都相等n每个外角的度数=360°.×n每个内角的度数=内角和.×练习册 22.1(2)
