21.3 可化为一元二次方程的分式方程(1) 课件(14张PPT)
文档属性
| 名称 | 21.3 可化为一元二次方程的分式方程(1) 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览





文档简介
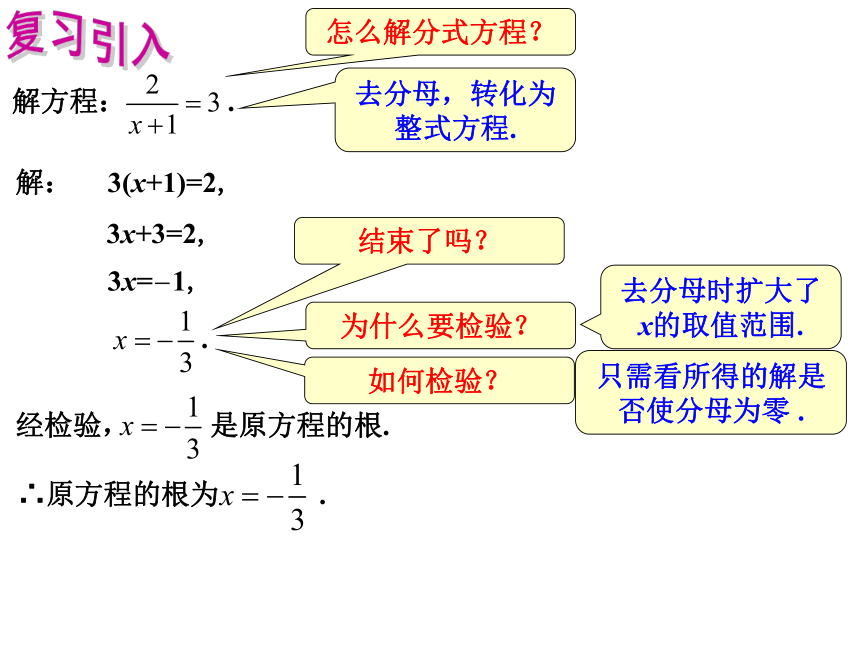
课件14张PPT。21.3 可化为一元二次方程的分式方程(1)复习引入什么是分式方程 ? 如果方程中只含分式和整式,且分母中含有未知数,那么这个方程叫做分式方程. 反馈练习1:下列关于x的方程中,哪些是分式方程? (1) ; ( ) (2) ; ( ) (3) ; ( ) (4) ; ( ) √√×√(5) ; ( ) (6) ; ( ) ××复习引入解方程: . 怎么解分式方程?去分母,转化为整式方程.解: 3(x+1)=2, 3x+3=2, 3x=-1, .结束了吗?为什么要检验?如何检验?经检验, 是原方程的根. ∴原方程的根为 .去分母时扩大了x的取值范围.只需看所得的解是否使分母为零 .适时小结解可化为一元一次方程的分式方程的一般步骤为 : ①去分母,将分式方程化为整式方程; ②解整式方程; ③检验所得解是否为原方程的根; ④写出原方程的根. 新课讲解问题:某单位共青团员们准备捐款1200元帮助结对的边远地区贫困
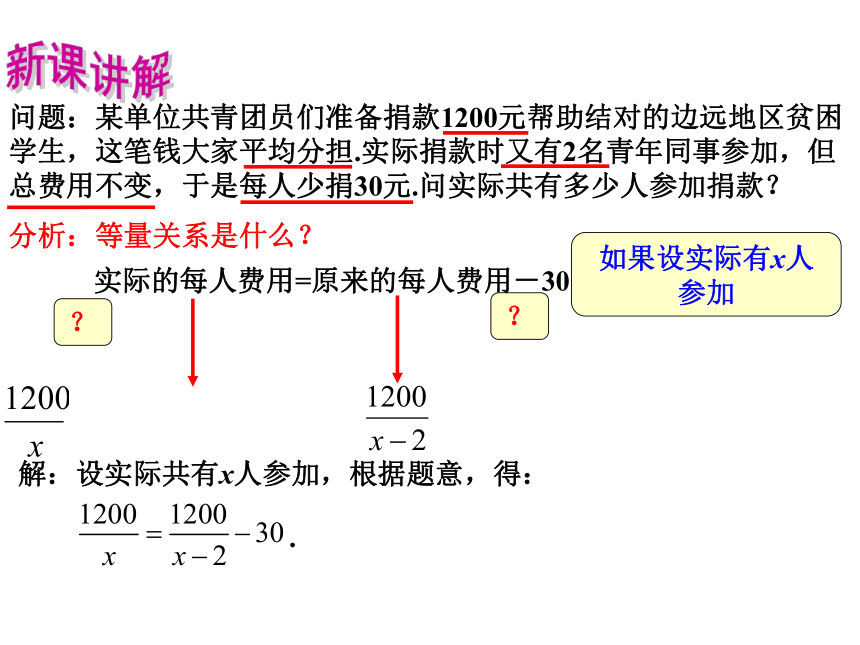
学生,这笔钱大家平均分担.实际捐款时又有2名青年同事参加,但
总费用不变,于是每人少捐30元.问实际共有多少人参加捐款?分析:等量关系是什么?实际的每人费用=原来的每人费用-30如果设实际有x人参加??解:设实际共有x人参加,根据题意,得: .新课讲解问题:某单位共青团员们准备捐款1200元帮助结对的边远地区贫困
学生,这笔钱大家平均分担.实际捐款时又有2名青年同事参加,但
总费用不变,于是每人少捐30元.问实际共有多少人参加捐款?解:设实际共有x人参加,根据题意,得: .怎么解分式方程?去分母,转化为整式方程.怎么去分母?方程两边同乘以最简公分母 .,.这是几元几次方程?..结束了吗?如何检验?检验:当 时,当 时,检验结束了吗?经检验:x1、 x2都是原方程的根,但x2=-8不符合题意,舍去. 答:实际共有10人参加. 方程两边同时乘以 x(x-2),得:可化为一元二次方程的分式方程:整理,得:适时小结解可化为一元二次方程的分式方程的一般步骤为 : ①去分母(找最简公分母) ,将分式方程化为整式方程; ②解整式方程; ③检验(在实际问题中还要看解是否满足实际意义 ) ; ④写出原方程的根. 新课讲解例1、解方程: . 怎么解方程?去分母,转化为整式方程.解:方程两边同时乘以(1-x)(1+x),得:结束了吗?如何检验?∴原方程的根为 .如何去分母?方程两边同乘以最简公分母 .整理,得: , 解得: . 检验:当 时, . 当 时,.新课讲解例2、解方程: . 最简公分母是什么?解:方程两边同时乘以(x-1)(x+1),得: ∴原方程的根为 .如何确定最简公分母?整理,得: , 解得: . 检验:当 时, . 当 时,.分母先要因式分解 .∴ 是原方程的增根,舍去. 适时小结解分式方程时要注意: 1.去分母时,常数项不能漏乘;2.当分母是二次多项式时,一般要先分解因式,
再找最简公分母. 例1、解方程: . 解:方程两边同时乘以(1-x)(1+x),得:例2、解方程: . 解:方程两边同时乘以(x-1)(x+1),得: 巩固练习1、解方程: . 解: , ∴原方程的根为 .整理,得: , 解得: . 检验:当 时, . 巩固练习2、解方程: . 解: , ∴原方程的根为 .整理,得: , 解得: . 检验:当 时, . 当 时,.自主小结解可化为一元二次方程的分式方程的一般步骤:
解分式方程的注意事项:
①去分母; ②解整式方程; ③检验; ④写出原方程的根. ①常数项不要漏乘; ②要正确找出最简公分母. 回家作业《导学案》习题21.3(1)
学生,这笔钱大家平均分担.实际捐款时又有2名青年同事参加,但
总费用不变,于是每人少捐30元.问实际共有多少人参加捐款?分析:等量关系是什么?实际的每人费用=原来的每人费用-30如果设实际有x人参加??解:设实际共有x人参加,根据题意,得: .新课讲解问题:某单位共青团员们准备捐款1200元帮助结对的边远地区贫困
学生,这笔钱大家平均分担.实际捐款时又有2名青年同事参加,但
总费用不变,于是每人少捐30元.问实际共有多少人参加捐款?解:设实际共有x人参加,根据题意,得: .怎么解分式方程?去分母,转化为整式方程.怎么去分母?方程两边同乘以最简公分母 .,.这是几元几次方程?..结束了吗?如何检验?检验:当 时,当 时,检验结束了吗?经检验:x1、 x2都是原方程的根,但x2=-8不符合题意,舍去. 答:实际共有10人参加. 方程两边同时乘以 x(x-2),得:可化为一元二次方程的分式方程:整理,得:适时小结解可化为一元二次方程的分式方程的一般步骤为 : ①去分母(找最简公分母) ,将分式方程化为整式方程; ②解整式方程; ③检验(在实际问题中还要看解是否满足实际意义 ) ; ④写出原方程的根. 新课讲解例1、解方程: . 怎么解方程?去分母,转化为整式方程.解:方程两边同时乘以(1-x)(1+x),得:结束了吗?如何检验?∴原方程的根为 .如何去分母?方程两边同乘以最简公分母 .整理,得: , 解得: . 检验:当 时, . 当 时,.新课讲解例2、解方程: . 最简公分母是什么?解:方程两边同时乘以(x-1)(x+1),得: ∴原方程的根为 .如何确定最简公分母?整理,得: , 解得: . 检验:当 时, . 当 时,.分母先要因式分解 .∴ 是原方程的增根,舍去. 适时小结解分式方程时要注意: 1.去分母时,常数项不能漏乘;2.当分母是二次多项式时,一般要先分解因式,
再找最简公分母. 例1、解方程: . 解:方程两边同时乘以(1-x)(1+x),得:例2、解方程: . 解:方程两边同时乘以(x-1)(x+1),得: 巩固练习1、解方程: . 解: , ∴原方程的根为 .整理,得: , 解得: . 检验:当 时, . 巩固练习2、解方程: . 解: , ∴原方程的根为 .整理,得: , 解得: . 检验:当 时, . 当 时,.自主小结解可化为一元二次方程的分式方程的一般步骤:
解分式方程的注意事项:
①去分母; ②解整式方程; ③检验; ④写出原方程的根. ①常数项不要漏乘; ②要正确找出最简公分母. 回家作业《导学案》习题21.3(1)
