21.4 无理方程(1) 课件(13张PPT)
文档属性
| 名称 | 21.4 无理方程(1) 课件(13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 118.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 15:08:26 | ||
图片预览




文档简介
课件13张PPT。21.4 无理方程(1)一.问题引入1.问题 在平面直角坐标系中,点A在x轴上,它与点B(-1,3)之间的距离为5,求点A的坐标?若设点A(x,0),特点:含有根式 根号内含有未知数无理方程是一个方程 可得:二.学习新知识1.无理方程 方程中含有根式,且被开方数是含有未知
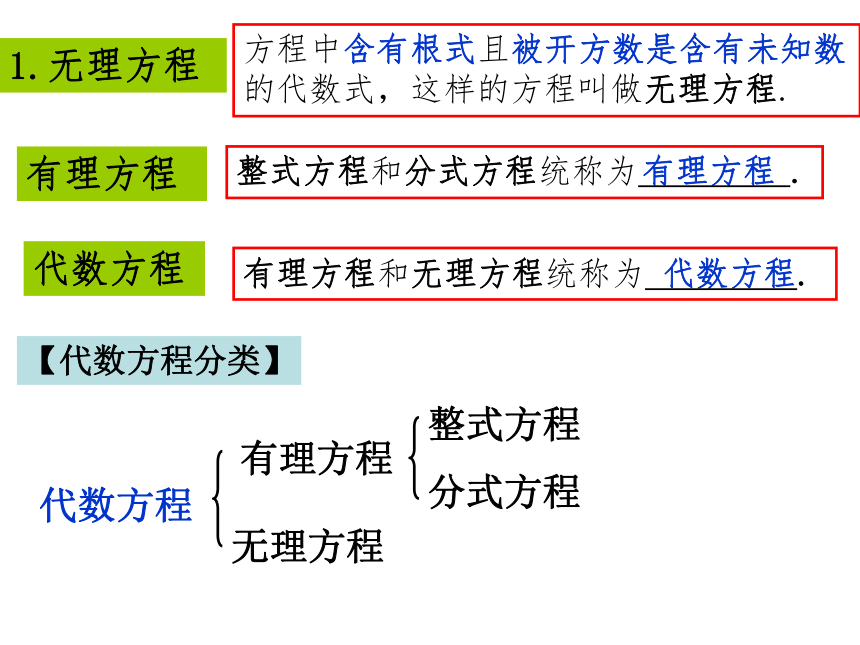
数的代数式,这样的方程叫做无理方程.(1)、(3)、(4)根号内含有未知数的方程是无理方程代数方程 有理方程 1.无理方程 方程中含有根式且被开方数是含有未知数
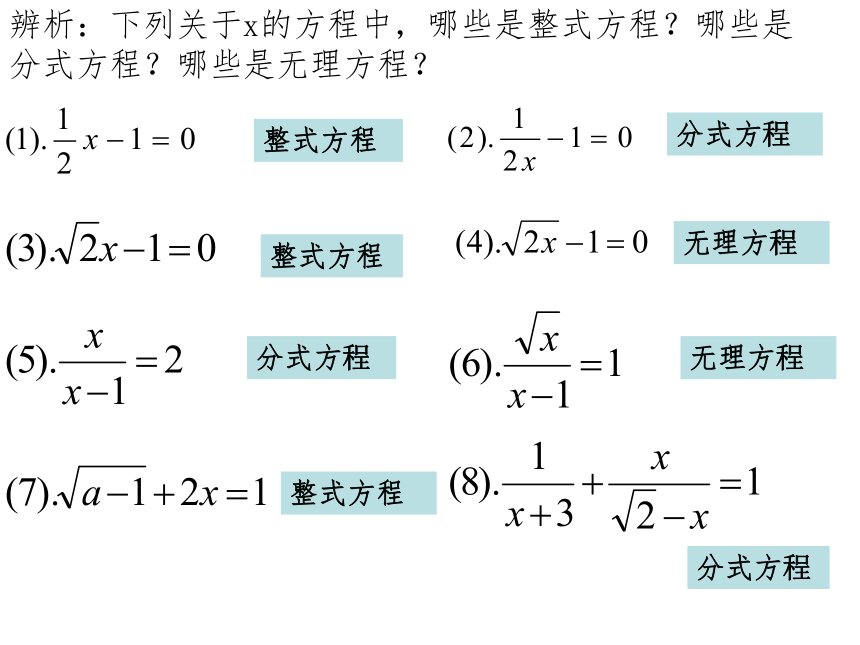
的代数式,这样的方程叫做无理方程.有理方程 整式方程和分式方程统称为 . 代数方程 有理方程和无理方程统称为 . 【代数方程分类】代数方程辨析:下列关于x的方程中,哪些是整式方程?哪些是分式方程?哪些是无理方程?整式方程分式方程无理方程分式方程整式方程无理方程整式方程分式方程例1.检验x=4,x=-1是不是方程 的解.2.思考和尝试如何解方程关键是如何去掉“根号”=a方程两边平方得:整理得:解得:都是原方程的解吗?检验左边=【检验】当x=4时4右边==4∴左边=右边当x=-1时左边=-1右边==1∴左边≠右边解简单的无理方程的一般步骤 方程两边平方代入无理方程的左、右两边若左边=右边,是原方程的根;若左边≠右边,是原方程的增根,舍去.解方程使这个二次根式单独在方程的一边练习:p42学习收获1.无理方程的概念.2.解无理方程.(1)方法:方程两边平方.(2)检验:代入原方程的左、右两边.
数的代数式,这样的方程叫做无理方程.(1)、(3)、(4)根号内含有未知数的方程是无理方程代数方程 有理方程 1.无理方程 方程中含有根式且被开方数是含有未知数
的代数式,这样的方程叫做无理方程.有理方程 整式方程和分式方程统称为 . 代数方程 有理方程和无理方程统称为 . 【代数方程分类】代数方程辨析:下列关于x的方程中,哪些是整式方程?哪些是分式方程?哪些是无理方程?整式方程分式方程无理方程分式方程整式方程无理方程整式方程分式方程例1.检验x=4,x=-1是不是方程 的解.2.思考和尝试如何解方程关键是如何去掉“根号”=a方程两边平方得:整理得:解得:都是原方程的解吗?检验左边=【检验】当x=4时4右边==4∴左边=右边当x=-1时左边=-1右边==1∴左边≠右边解简单的无理方程的一般步骤 方程两边平方代入无理方程的左、右两边若左边=右边,是原方程的根;若左边≠右边,是原方程的增根,舍去.解方程使这个二次根式单独在方程的一边练习:p42学习收获1.无理方程的概念.2.解无理方程.(1)方法:方程两边平方.(2)检验:代入原方程的左、右两边.
