21.4 无理方程(2) 课件(14张PPT)
文档属性
| 名称 | 21.4 无理方程(2) 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 289.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览






文档简介
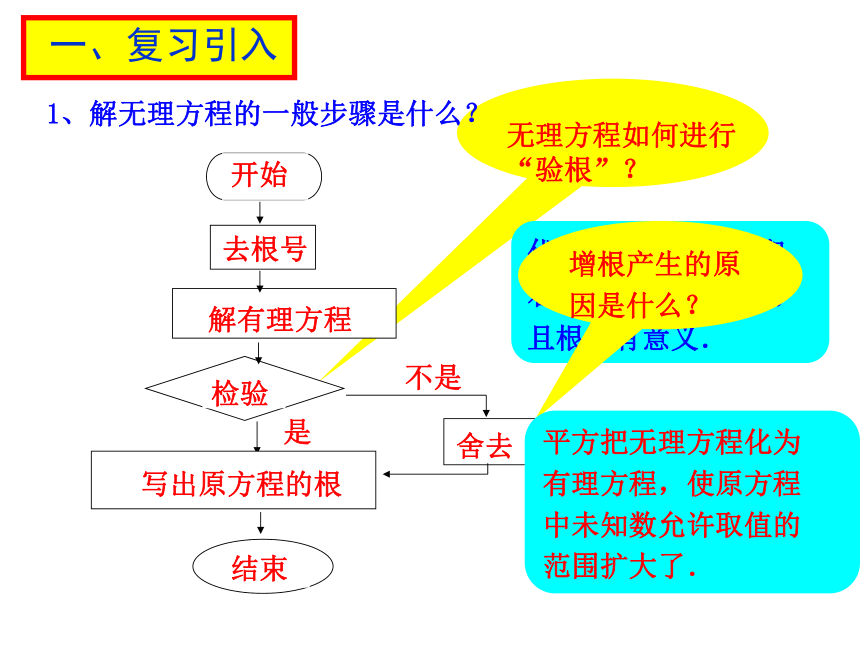
课件14张PPT。21.4无理方程(2) 一、复习引入1、解无理方程的一般步骤是什么? 是开始去根号无理方程如何进行“验根”?代入原方程的左边和
右边,使左边=右边,
且根号有意义. 增根产生的原因是什么? 平方把无理方程化为
有理方程,使原方程
中未知数允许取值的
范围扩大了. 不是 二、新课教学例1 解下列方程:(1)如何化为有理方程?方程两边平方 . 解:别忘记平方 将方程化为一般形式 . 采用因式分解法. 都是原方程的根吗? 当 x=4时.右边=-2,可知x=4是增根,舍去.
当 x=12,右边=左边=6,
可知x=12是原方程的根. 经检验:x=4是增根,舍去;
x=12是原方程的根..
所以原方程的根是x=12..一般将“根号项”放在方程的一边,
把其他“项”放在方程的另一边.
二、新课教学例1 解下列方程:(2)可以直接平方去根号吗?方程两边平方 . 解:转化为等号一边含根号,等号另一边不含根号.都是原方程的根吗? 当 x=6时.左边=0,右边=-3,可知x=6是增根,
舍去.当 x=2,右边=左边=1,
可知x=2是原方程的根. 经检验x=6,是增根,舍去;
x=2是原方程的根..
所以原方程的根是x=2..解只含一个“根号”的无理方程时:两边平方,化为有理方程.
※课堂练习1 (1)(2)解下列方程: 二、新课教学例2 解下列方程:(1)可以直接平方去根号吗?方程两边可以直接平方 . 解:将方程化为一般形式 . 采用因式分解法. 都是原方程的根吗? 当 x=-1时.左边无意义,可知x=-1是增根,
舍去.当 x=3,右边=左边,
可知x=3是原方程的根. 经检验:x=-1是增根,舍去;
x=3是原方程的根..
所以原方程的根是x=3..解含有两个“根号”的无理方程时: 二、新课教学例2 解下列方程:(2)如何转化为有理方程?方程两边平方 . 解:通过移项使等号两边各含一个根号再平方较简单.将方程整理化为只含一个根号 . 是原方程的根吗? .一般将两个“根号项”分别放在等号两边.两边平方后再整理.
第二次平方,把原方程转化为有理方程.课堂练习 2(1)(2)解下列方程:课堂练习 2(3) 思考不解方程你能判断这个方程实数根的情况吗? 是一个非负数 左边=一个非负数+1>0,右边=0,
所以原方程没有实数根. 归纳课堂练习3 下列方程中,有实数根的方程是:( ) (A) (B)
(C) (D)
C 是一个非负数 ……请谈谈你的收获课堂小结 1、解只含一个“根号”的无理方程时:
2、解只含两个“根号”的无理方程时:
将“根号项”放在方程的一边其它“项”放在方程的另一边然后进行平方,化为有理方程.将两个“根号项”分别放在等号两边两边平方后再整理,简化解题过程.如果含两个“根号”的无理方程中还有其它“项”,
通常要经过两次平方,把原方程转化为有理方程.作业布置
练习册 习题21.4(2)
右边,使左边=右边,
且根号有意义. 增根产生的原因是什么? 平方把无理方程化为
有理方程,使原方程
中未知数允许取值的
范围扩大了. 不是 二、新课教学例1 解下列方程:(1)如何化为有理方程?方程两边平方 . 解:别忘记平方 将方程化为一般形式 . 采用因式分解法. 都是原方程的根吗? 当 x=4时.右边=-2,可知x=4是增根,舍去.
当 x=12,右边=左边=6,
可知x=12是原方程的根. 经检验:x=4是增根,舍去;
x=12是原方程的根..
所以原方程的根是x=12..一般将“根号项”放在方程的一边,
把其他“项”放在方程的另一边.
二、新课教学例1 解下列方程:(2)可以直接平方去根号吗?方程两边平方 . 解:转化为等号一边含根号,等号另一边不含根号.都是原方程的根吗? 当 x=6时.左边=0,右边=-3,可知x=6是增根,
舍去.当 x=2,右边=左边=1,
可知x=2是原方程的根. 经检验x=6,是增根,舍去;
x=2是原方程的根..
所以原方程的根是x=2..解只含一个“根号”的无理方程时:两边平方,化为有理方程.
※课堂练习1 (1)(2)解下列方程: 二、新课教学例2 解下列方程:(1)可以直接平方去根号吗?方程两边可以直接平方 . 解:将方程化为一般形式 . 采用因式分解法. 都是原方程的根吗? 当 x=-1时.左边无意义,可知x=-1是增根,
舍去.当 x=3,右边=左边,
可知x=3是原方程的根. 经检验:x=-1是增根,舍去;
x=3是原方程的根..
所以原方程的根是x=3..解含有两个“根号”的无理方程时: 二、新课教学例2 解下列方程:(2)如何转化为有理方程?方程两边平方 . 解:通过移项使等号两边各含一个根号再平方较简单.将方程整理化为只含一个根号 . 是原方程的根吗? .一般将两个“根号项”分别放在等号两边.两边平方后再整理.
第二次平方,把原方程转化为有理方程.课堂练习 2(1)(2)解下列方程:课堂练习 2(3) 思考不解方程你能判断这个方程实数根的情况吗? 是一个非负数 左边=一个非负数+1>0,右边=0,
所以原方程没有实数根. 归纳课堂练习3 下列方程中,有实数根的方程是:( ) (A) (B)
(C) (D)
C 是一个非负数 ……请谈谈你的收获课堂小结 1、解只含一个“根号”的无理方程时:
2、解只含两个“根号”的无理方程时:
将“根号项”放在方程的一边其它“项”放在方程的另一边然后进行平方,化为有理方程.将两个“根号项”分别放在等号两边两边平方后再整理,简化解题过程.如果含两个“根号”的无理方程中还有其它“项”,
通常要经过两次平方,把原方程转化为有理方程.作业布置
练习册 习题21.4(2)
