21.7 列方程(组)解应用题(1) 课件(14张PPT)
文档属性
| 名称 | 21.7 列方程(组)解应用题(1) 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 85.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览






文档简介
课件14张PPT。21.7列方程(组)解应用题(1)活动一:回忆与思考 据报道,某地乐天玛特原来平均每天的客流量可达20000人,但“萨德”事件后两天,客流量减少到了5800人.假设这两天客流量降低的百分率相同,
设每天客流量降低的百分率为x,
可列方程 .活动一:回忆与思考 一家本土超市2017年2月28日前日平均营业额为5000万元,“萨德”事件后日营业额连续上涨,到3月2日日营业额达到7200万元,假设每天的增长率相同,
设日增长率为x,
可列方程 .
.
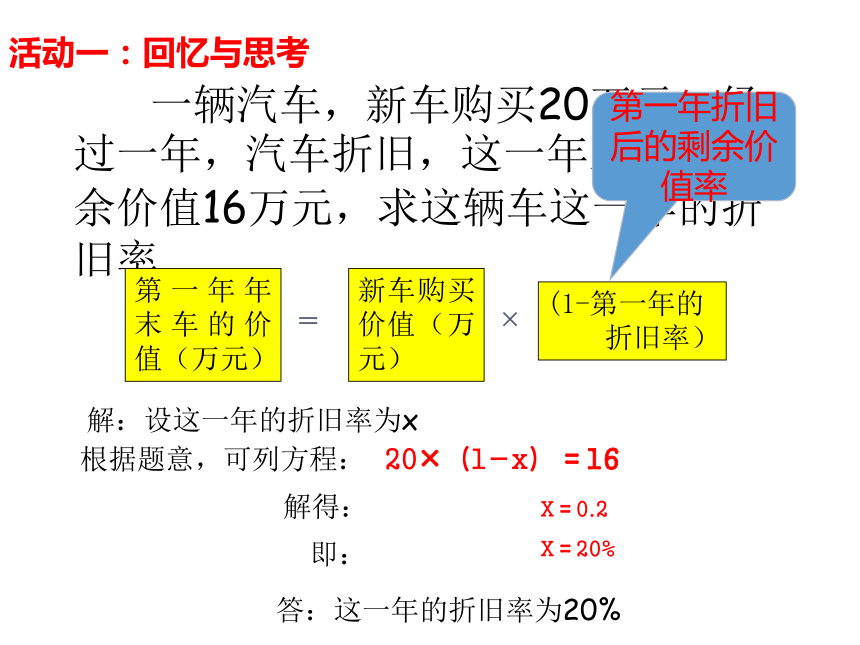
增长率问题:现有产量为a,年平均增长率为x,经过n年后,产量= . 降低率问题:现有产量为a,年平均降低率为x,经过n年后,产量= . 活动一:回忆与思考 一辆汽车,新车购买20万元,经过一年,汽车折旧,这一年末汽车剩余价值16万元,求这辆车这一年的折旧率.解:设这一年的折旧率为x答:这一年的折旧率为20%第一年折旧后的剩余价值率列方程(组)解应用题的一般步骤是:审题;
设元;
列方程(组);
解方程(组);
检验;
解释.活动一:回忆与思考活动二:新知和巩固例题1 一辆汽车,新车购买20万元,第一年、第二年的年折旧率相同,已知第二年末这辆车折旧后价值12.8万元,求这辆车的年折旧率.第一、二年两次折旧后的剩余价值率一辆汽车,新车购买价20万元,第一年使用后折旧20%,以后该车的年折旧率有所变化,但它在第二、三年的年折旧率相同。已知在第三年年末,这辆车折旧后价值11.56万元,求这辆车第二、三年的年折旧率。第三年末车的价值新车购买价第一年折旧后的剩余价值率第二、三年两次折旧后的剩余价值率=××活动二:新知和巩固变式训练活动二:新知和巩固例题2 为了更好的提高业务水平,某商场进行品牌调整,其中某品牌原来租用的长为16米宽为5米的长方形展示区调整长比宽多2米,总面积不变,那么长和宽各为多少米?变式训练 该品牌场地调整后,重新装修,需要制作96个一样大小的正方体模型装饰,准备用一块长128厘米,宽64厘米,高48厘米的长方体木材来下料.经生产设计师的精心设计,若不计损耗,则该木材恰好用完,没有剩余.求每个正方体模型的棱长是多少厘米?活动二:新知和巩固活动三:自主练习 在一块长方形镜面玻璃的四周,镶上与它的周长相等的边框,制成一面镜子,镜子的长与宽的比是3:1.已知镜面玻璃的价格是每平方米100元,边框的价格是每米20元,另外制作这面镜子还需要加工费55元.如果制作这面镜子共花了210元,那么这面镜子的长和宽分别是多少米?100 ×3x ×x解:设这面镜子的长为3x米,宽为x米。活动四:本课小结 “经过这节课的学习,你有哪些收获?还有什么困惑吗?”活动五:拓展练习数字问题:周瑜的年龄.
大江东去浪涛尽,千古风流数人物.
而立之年都东吴,早逝英年两位数.
十比个位恰小三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?
活动六:作业布置甲乙丙必做题:练习册27.1(1)
选做题:
如图:有一长方形的地,长为x米,宽为120米,(x>120),建筑商将它分为甲、乙、丙三部分,甲和乙为正方形.现计划甲建成住宅区,乙建成商场,丙开辟成公园,若已知丙地的面积为3200平方米,试求x的值.
x
完成课上只列式的应用题。
设每天客流量降低的百分率为x,
可列方程 .活动一:回忆与思考 一家本土超市2017年2月28日前日平均营业额为5000万元,“萨德”事件后日营业额连续上涨,到3月2日日营业额达到7200万元,假设每天的增长率相同,
设日增长率为x,
可列方程 .
.
增长率问题:现有产量为a,年平均增长率为x,经过n年后,产量= . 降低率问题:现有产量为a,年平均降低率为x,经过n年后,产量= . 活动一:回忆与思考 一辆汽车,新车购买20万元,经过一年,汽车折旧,这一年末汽车剩余价值16万元,求这辆车这一年的折旧率.解:设这一年的折旧率为x答:这一年的折旧率为20%第一年折旧后的剩余价值率列方程(组)解应用题的一般步骤是:审题;
设元;
列方程(组);
解方程(组);
检验;
解释.活动一:回忆与思考活动二:新知和巩固例题1 一辆汽车,新车购买20万元,第一年、第二年的年折旧率相同,已知第二年末这辆车折旧后价值12.8万元,求这辆车的年折旧率.第一、二年两次折旧后的剩余价值率一辆汽车,新车购买价20万元,第一年使用后折旧20%,以后该车的年折旧率有所变化,但它在第二、三年的年折旧率相同。已知在第三年年末,这辆车折旧后价值11.56万元,求这辆车第二、三年的年折旧率。第三年末车的价值新车购买价第一年折旧后的剩余价值率第二、三年两次折旧后的剩余价值率=××活动二:新知和巩固变式训练活动二:新知和巩固例题2 为了更好的提高业务水平,某商场进行品牌调整,其中某品牌原来租用的长为16米宽为5米的长方形展示区调整长比宽多2米,总面积不变,那么长和宽各为多少米?变式训练 该品牌场地调整后,重新装修,需要制作96个一样大小的正方体模型装饰,准备用一块长128厘米,宽64厘米,高48厘米的长方体木材来下料.经生产设计师的精心设计,若不计损耗,则该木材恰好用完,没有剩余.求每个正方体模型的棱长是多少厘米?活动二:新知和巩固活动三:自主练习 在一块长方形镜面玻璃的四周,镶上与它的周长相等的边框,制成一面镜子,镜子的长与宽的比是3:1.已知镜面玻璃的价格是每平方米100元,边框的价格是每米20元,另外制作这面镜子还需要加工费55元.如果制作这面镜子共花了210元,那么这面镜子的长和宽分别是多少米?100 ×3x ×x解:设这面镜子的长为3x米,宽为x米。活动四:本课小结 “经过这节课的学习,你有哪些收获?还有什么困惑吗?”活动五:拓展练习数字问题:周瑜的年龄.
大江东去浪涛尽,千古风流数人物.
而立之年都东吴,早逝英年两位数.
十比个位恰小三,个位平方与寿符.
哪位学子算得快,多少年华属周瑜?
活动六:作业布置甲乙丙必做题:练习册27.1(1)
选做题:
如图:有一长方形的地,长为x米,宽为120米,(x>120),建筑商将它分为甲、乙、丙三部分,甲和乙为正方形.现计划甲建成住宅区,乙建成商场,丙开辟成公园,若已知丙地的面积为3200平方米,试求x的值.
x
完成课上只列式的应用题。
