22.2(2)平行四边形 课件(16张PPT)
文档属性
| 名称 | 22.2(2)平行四边形 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 233.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览

文档简介
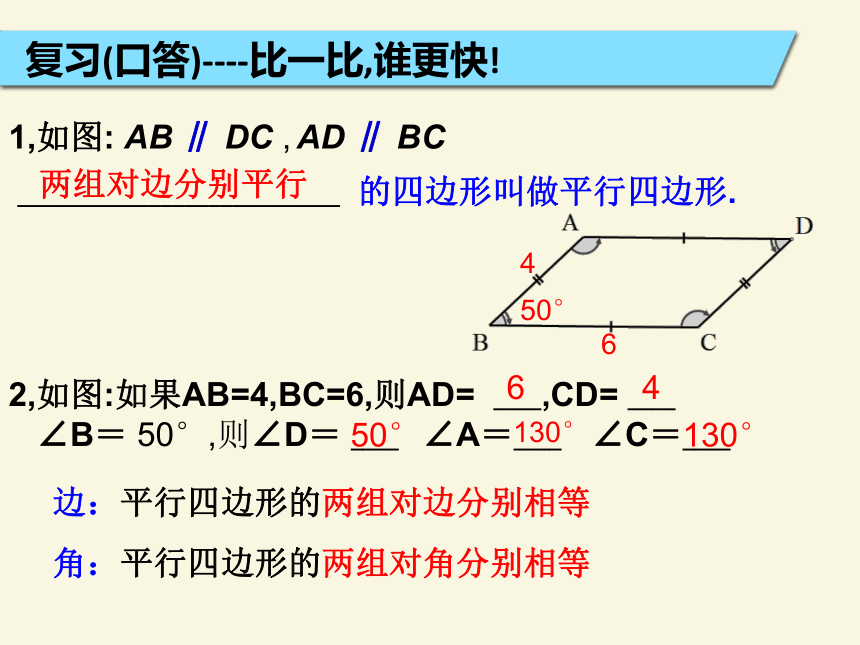
课件16张PPT。§22.2 平行四边形(2)复习(口答)----比一比,谁更快!1,如图: AB ∥ DC , ___________________________ 的四边形叫做平行四边形. 2,如图:如果AB=4,BC=6,则AD= ____,CD= ____
∠B= 50°,则∠D= ____ ∠A=____ ∠C=____
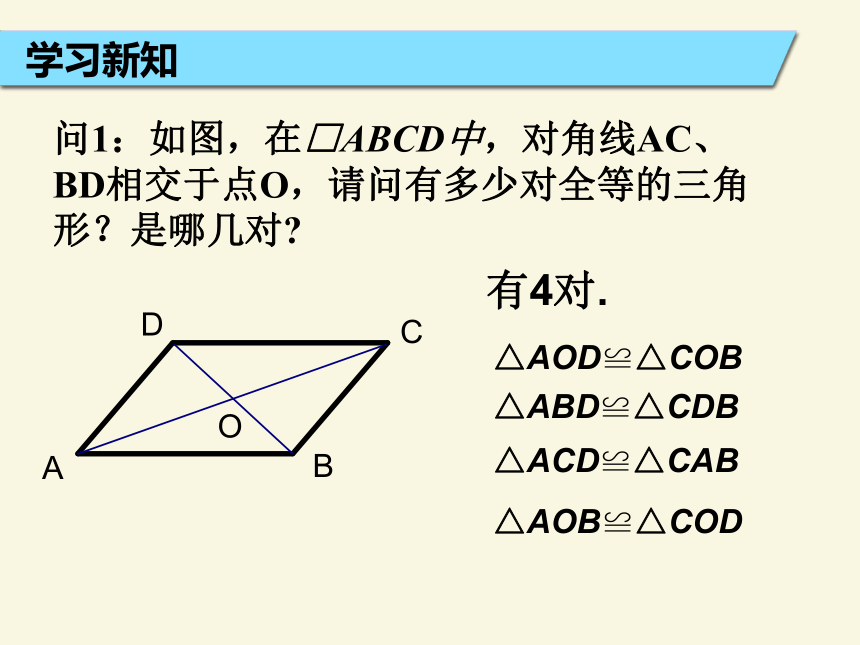
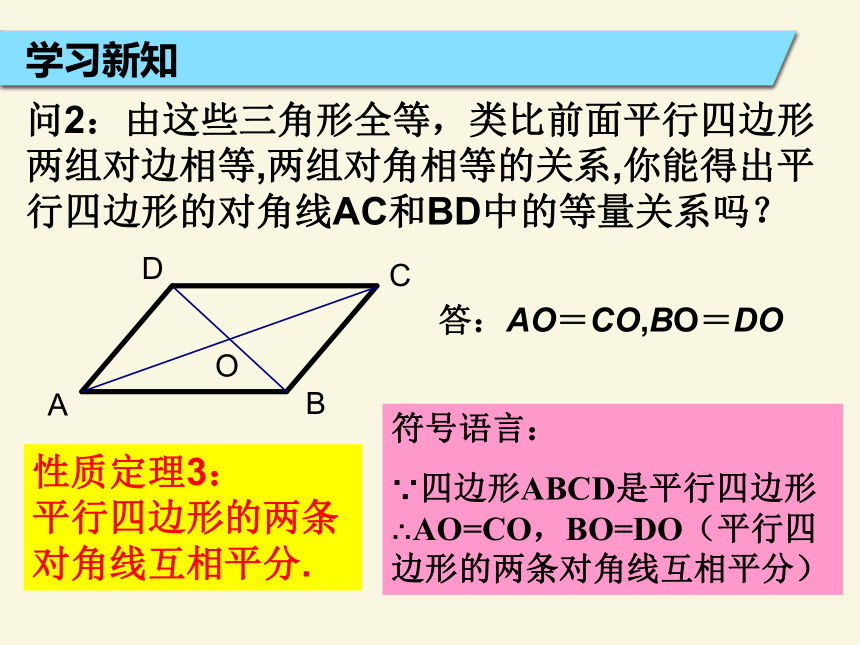
角:平行四边形的两组对角分别相等AD ∥ BC两组对边分别平行边:平行四边形的两组对边分别相等4650°6450°130°130°学习新知问1:如图,在□ABCD中,对角线AC、BD相交于点O,请问有多少对全等的三角形?是哪几对?有4对.△ABD≌△CDB△AOD≌△COB△AOB≌△COD△ACD≌△CAB问2:由这些三角形全等,类比前面平行四边形两组对边相等,两组对角相等的关系,你能得出平行四边形的对角线AC和BD中的等量关系吗? 学习新知答:AO=CO,BO=DO 性质定理3:
平行四边形的两条对角线互相平分. 符号语言:
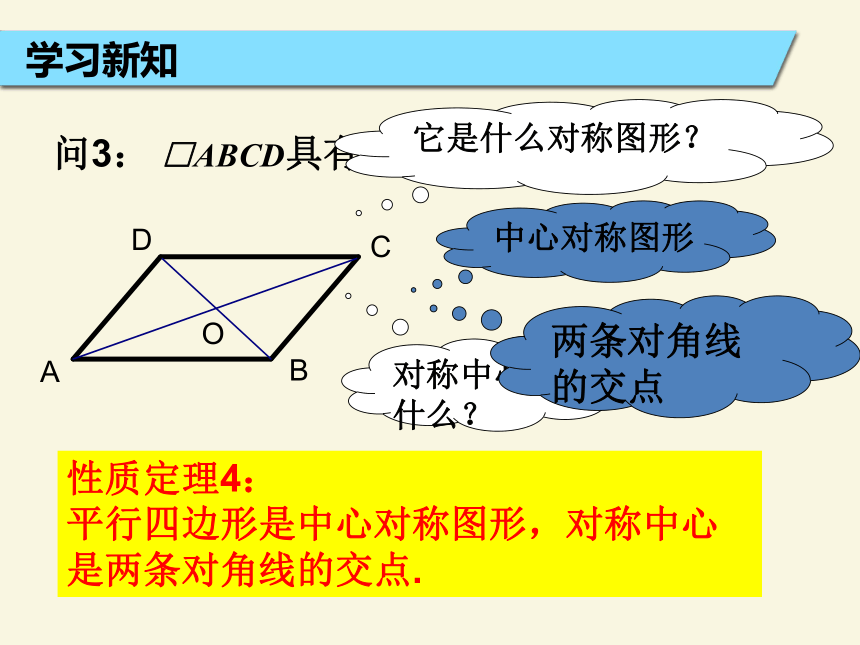
∵四边形ABCD是平行四边形∴AO=CO,BO=DO(平行四边形的两条对角线互相平分)问3: □ABCD具有某种对称性吗?性质定理4:
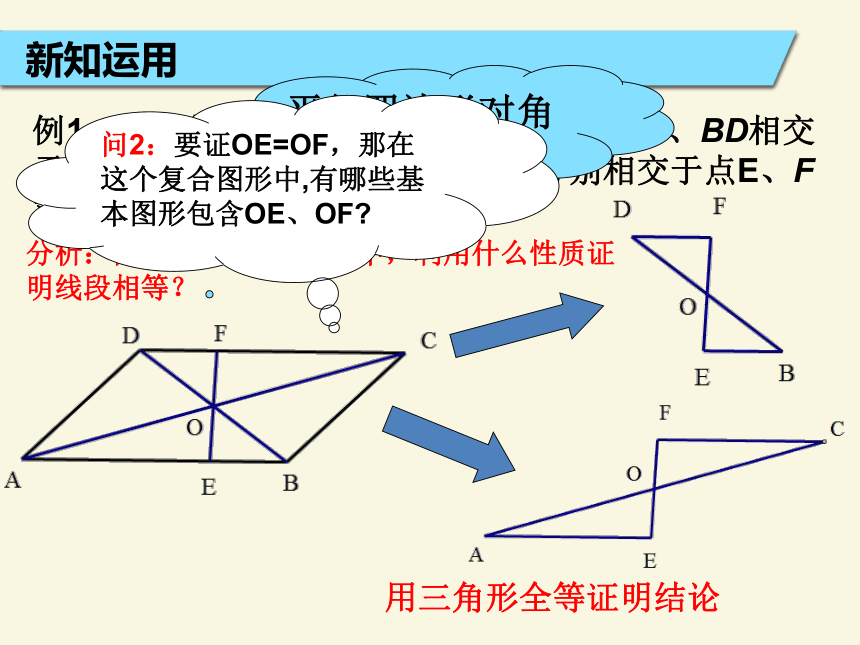
平行四边形是中心对称图形,对称中心是两条对角线的交点. 学习新知它是什么对称图形?中心对称图形对称中心是什么?两条对角线的交点新知运用 例1,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF 分析:问1:在平行四边形中,利用什么性质证明线段相等?用三角形全等证明结论 平行四边形对角线互相平分问2:要证OE=OF,那在这个复合图形中,有哪些基本图形包含OE、OF?
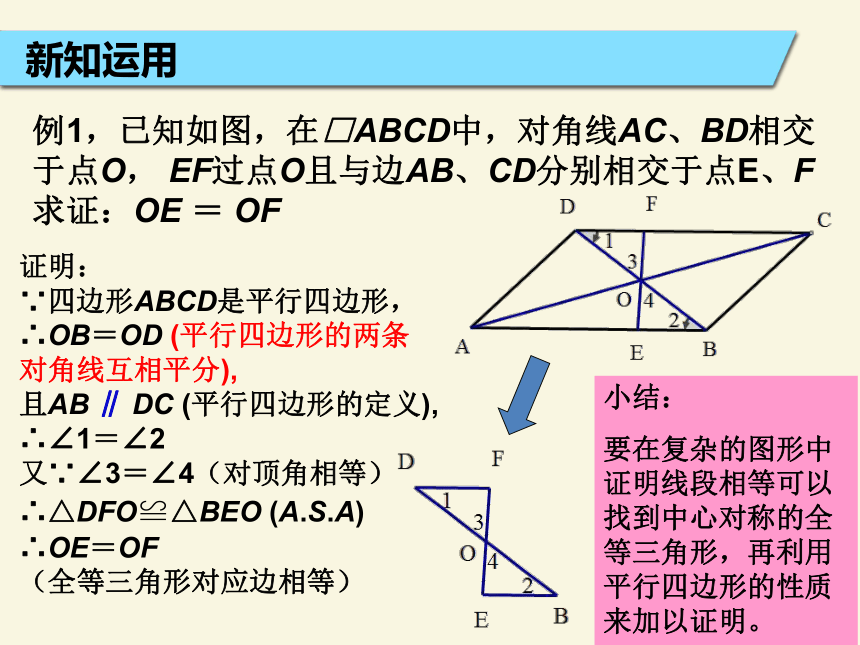
新知运用 例1,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF 证明:
∵四边形ABCD是平行四边形,
∴OB=OD (平行四边形的两条对角线互相平分),
且AB ∥ DC (平行四边形的定义),
∴∠1=∠2
又∵∠3=∠4(对顶角相等)
∴△DFO≌△BEO (A.S.A)
∴OE=OF
(全等三角形对应边相等)小结:
要在复杂的图形中证明线段相等可以找到中心对称的全等三角形,再利用平行四边形的性质来加以证明。例2,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE ∥ CF
求证:∠BAE = ∠DCF 新知运用 分析:
问1:在平行四边形中,要证明∠BAE = ∠DCF,利用什么性质证明角相等?答:平行四边形对角相等问2:图中有哪些平行四边形?例2,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE ∥ CF
求证:∠BAE = ∠DCF 新知运用 证明:
∵四边形ABCD是平行四边形,
∴AD ∥ BC (平行四边形的定义)
∠BAD=∠DCB
(平行四边形的对角相等)
又∵AE ∥ CF
∴四边形AECF是平行四边形
(平行四边形的定义)
得∠1=∠2(平行四边形的对角相等)
∵∠3=∠BAD-∠1
∠4=∠DCB-∠2
∴∠3=∠4 即∠BAE = ∠DCF 是否还有其他的方法?证明:∵四边形ABCD是平行四边形
∴AB=CD(平行四边形对边相等)
∠B= ∠D(平行四边形对角相等)
∵ AE ∥ CF(已知)
∴ ∠AEB= ∠FCB(两直线平行,同位角相等)
∵四边形ABCD是平行四边形
∴AD ∥ BC(平行四边形的定义)
∴ ∠DFC= ∠FCB(两直线平行,内错角相等)
∴ ∠AEB= ∠DFC(等量代换)
在△ABE和△CDF中
∴ △ABE≌△CDF(A.A.S) ∴ ∠BAE = ∠DCF(全等三角形对应角相等) 新知运用 例2,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE ∥ CF.
求证:∠BAE = ∠DCF 课堂练习 1.□ABCD 中,AD= 6cm,AC = 10cm,BD = 6cm,ΔAOD的周长是多少?ΔAOD和ΔAOB的面积有什么关系?解:在□ABCD中,
(平行四边形两条对角线互相平分)答: ΔAOD的周长为14cm, ΔAOD和ΔAOB的面积相等。小结:平行四边形中有四组面积相等的三角形。Δ课堂练习 2.在平面直角坐标系中,□ABCD的对角线的交点正好与坐标原点重合,且点A、B的坐标分别为A (3,2)、B (– 2,1),试写出C、D两点的坐标. 解:
∵平行四边形是中心对称图形
∴点B和点D关于原点中心对称
∵B (–2,1)
∴D(2,-1)
同理:C(-3,-2)合作探究(我们最棒!)3.如图,在□ABCD中,点E、F分别是线段AC、CA延长线上的点,且CE=AF.
求证:BF∥DE.
O本课小结 通过这节课的学习,你有什么收获或体会?1.研究平行四边形的问题可以从边、角、对角线和对称性四个方面研究.
性质定理3:
平行四边形的两条对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO(平行四边形的两条对角线互相平分)
性质定理4:
平行四边形是中心对称图形,对称中心是两条对角线的交点.
2.解平行四边形题目的关键是,要在复杂的图形中找到中心对称的全等三角形,利用平行四边形的性质证明线段相等布置作业A组:
1.整理 “工作单”的内容;
2.完成练习册 习题22.2(2)
B组:拓展提高
1、一平行四边形两条对角线的长度分别为5cm和7cm,一边长为xcm,则x的取值范围是 .
2、在平面直角坐标系中,已知平行四边形的三个顶点为A(2,4),B(-1,1),C(3,1),则第四个顶点D的坐标是 .谢谢!
∠B= 50°,则∠D= ____ ∠A=____ ∠C=____
角:平行四边形的两组对角分别相等AD ∥ BC两组对边分别平行边:平行四边形的两组对边分别相等4650°6450°130°130°学习新知问1:如图,在□ABCD中,对角线AC、BD相交于点O,请问有多少对全等的三角形?是哪几对?有4对.△ABD≌△CDB△AOD≌△COB△AOB≌△COD△ACD≌△CAB问2:由这些三角形全等,类比前面平行四边形两组对边相等,两组对角相等的关系,你能得出平行四边形的对角线AC和BD中的等量关系吗? 学习新知答:AO=CO,BO=DO 性质定理3:
平行四边形的两条对角线互相平分. 符号语言:
∵四边形ABCD是平行四边形∴AO=CO,BO=DO(平行四边形的两条对角线互相平分)问3: □ABCD具有某种对称性吗?性质定理4:
平行四边形是中心对称图形,对称中心是两条对角线的交点. 学习新知它是什么对称图形?中心对称图形对称中心是什么?两条对角线的交点新知运用 例1,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF 分析:问1:在平行四边形中,利用什么性质证明线段相等?用三角形全等证明结论 平行四边形对角线互相平分问2:要证OE=OF,那在这个复合图形中,有哪些基本图形包含OE、OF?
新知运用 例1,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF 证明:
∵四边形ABCD是平行四边形,
∴OB=OD (平行四边形的两条对角线互相平分),
且AB ∥ DC (平行四边形的定义),
∴∠1=∠2
又∵∠3=∠4(对顶角相等)
∴△DFO≌△BEO (A.S.A)
∴OE=OF
(全等三角形对应边相等)小结:
要在复杂的图形中证明线段相等可以找到中心对称的全等三角形,再利用平行四边形的性质来加以证明。例2,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE ∥ CF
求证:∠BAE = ∠DCF 新知运用 分析:
问1:在平行四边形中,要证明∠BAE = ∠DCF,利用什么性质证明角相等?答:平行四边形对角相等问2:图中有哪些平行四边形?例2,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE ∥ CF
求证:∠BAE = ∠DCF 新知运用 证明:
∵四边形ABCD是平行四边形,
∴AD ∥ BC (平行四边形的定义)
∠BAD=∠DCB
(平行四边形的对角相等)
又∵AE ∥ CF
∴四边形AECF是平行四边形
(平行四边形的定义)
得∠1=∠2(平行四边形的对角相等)
∵∠3=∠BAD-∠1
∠4=∠DCB-∠2
∴∠3=∠4 即∠BAE = ∠DCF 是否还有其他的方法?证明:∵四边形ABCD是平行四边形
∴AB=CD(平行四边形对边相等)
∠B= ∠D(平行四边形对角相等)
∵ AE ∥ CF(已知)
∴ ∠AEB= ∠FCB(两直线平行,同位角相等)
∵四边形ABCD是平行四边形
∴AD ∥ BC(平行四边形的定义)
∴ ∠DFC= ∠FCB(两直线平行,内错角相等)
∴ ∠AEB= ∠DFC(等量代换)
在△ABE和△CDF中
∴ △ABE≌△CDF(A.A.S) ∴ ∠BAE = ∠DCF(全等三角形对应角相等) 新知运用 例2,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE ∥ CF.
求证:∠BAE = ∠DCF 课堂练习 1.□ABCD 中,AD= 6cm,AC = 10cm,BD = 6cm,ΔAOD的周长是多少?ΔAOD和ΔAOB的面积有什么关系?解:在□ABCD中,
(平行四边形两条对角线互相平分)答: ΔAOD的周长为14cm, ΔAOD和ΔAOB的面积相等。小结:平行四边形中有四组面积相等的三角形。Δ课堂练习 2.在平面直角坐标系中,□ABCD的对角线的交点正好与坐标原点重合,且点A、B的坐标分别为A (3,2)、B (– 2,1),试写出C、D两点的坐标. 解:
∵平行四边形是中心对称图形
∴点B和点D关于原点中心对称
∵B (–2,1)
∴D(2,-1)
同理:C(-3,-2)合作探究(我们最棒!)3.如图,在□ABCD中,点E、F分别是线段AC、CA延长线上的点,且CE=AF.
求证:BF∥DE.
O本课小结 通过这节课的学习,你有什么收获或体会?1.研究平行四边形的问题可以从边、角、对角线和对称性四个方面研究.
性质定理3:
平行四边形的两条对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
∴AO=CO,BO=DO(平行四边形的两条对角线互相平分)
性质定理4:
平行四边形是中心对称图形,对称中心是两条对角线的交点.
2.解平行四边形题目的关键是,要在复杂的图形中找到中心对称的全等三角形,利用平行四边形的性质证明线段相等布置作业A组:
1.整理 “工作单”的内容;
2.完成练习册 习题22.2(2)
B组:拓展提高
1、一平行四边形两条对角线的长度分别为5cm和7cm,一边长为xcm,则x的取值范围是 .
2、在平面直角坐标系中,已知平行四边形的三个顶点为A(2,4),B(-1,1),C(3,1),则第四个顶点D的坐标是 .谢谢!
