22.2(2)平行四边形 课件(22张PPT)
文档属性
| 名称 | 22.2(2)平行四边形 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 240.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览



文档简介
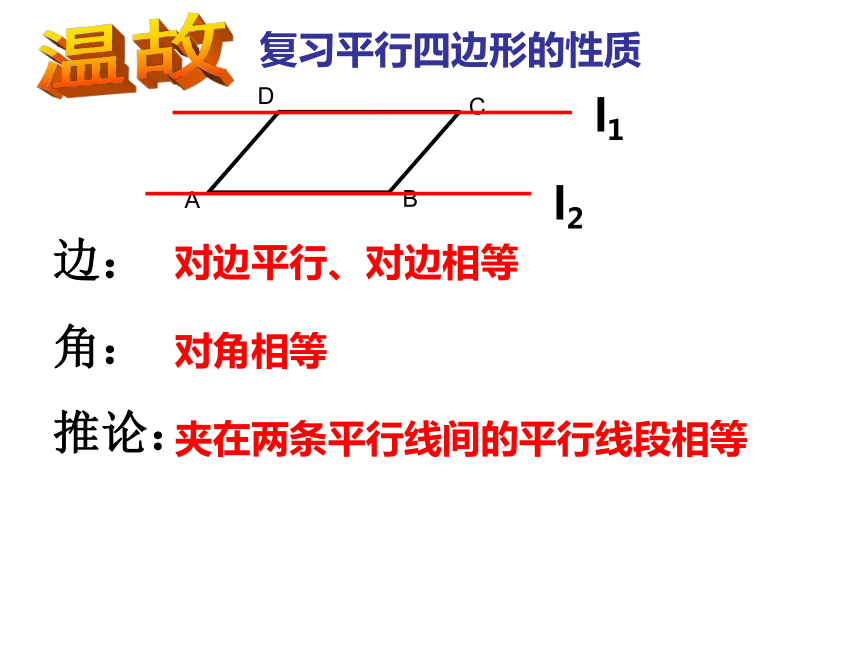
课件22张PPT。22.2(2)平行四边形复习平行四边形的性质边:
角:
推论:对边平行、对边相等对角相等夹在两条平行线间的平行线段相等l1l2温故(1)已知平行四边形两条邻边的比为2:5,周长为28cm,则这个平行四边形的四条边长分别为_____________________________.
(2)在□ABCD中,已知∠B+∠D=110°,则∠A=_____度,∠C=_____度.
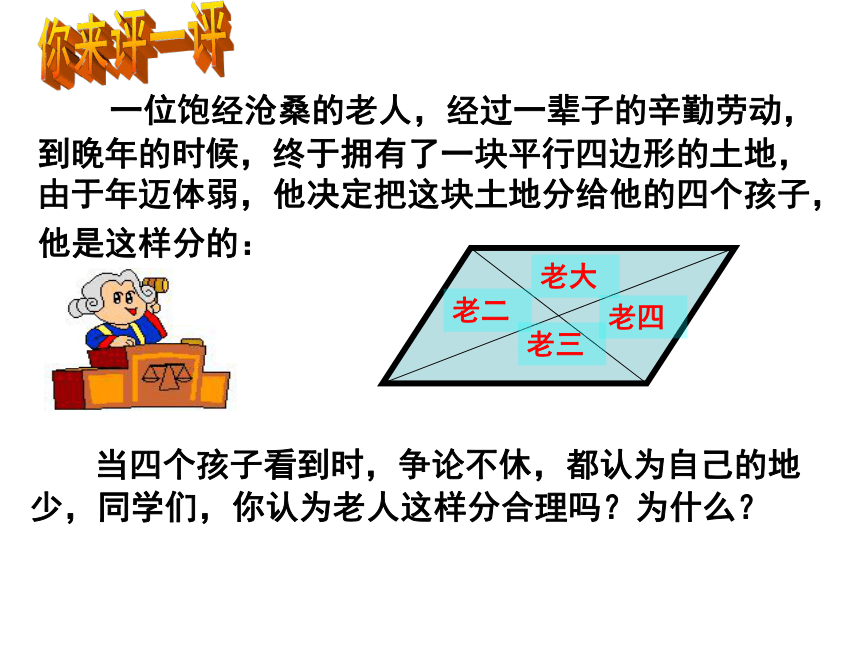
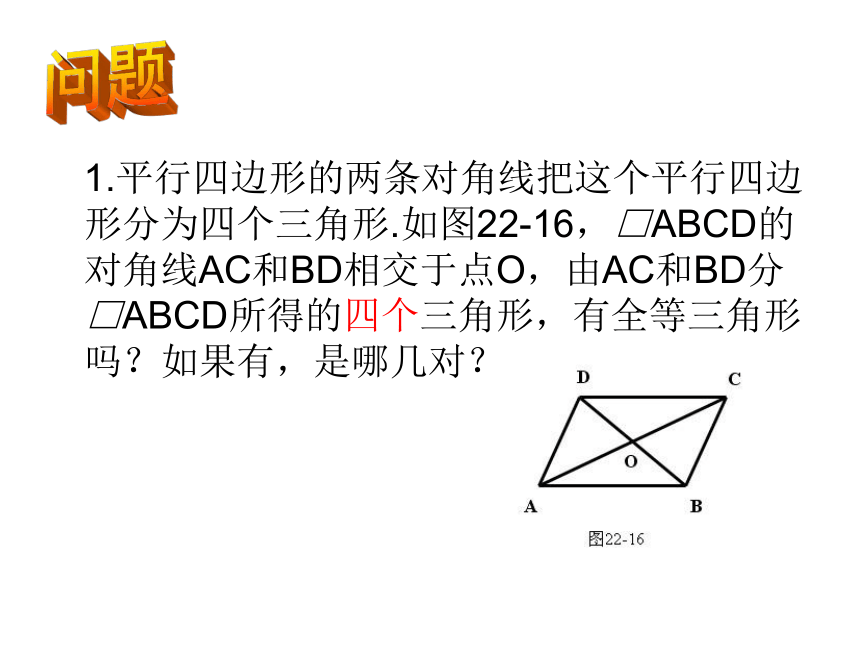
4cm,10cm,4cm,10cm125125例题复习你来评一评 一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的: 老大老二老三老四 当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么? 1.平行四边形的两条对角线把这个平行四边形分为四个三角形.如图22-16,□ABCD的对角线AC和BD相交于点O,由AC和BD分□ABCD所得的四个三角形,有全等三角形吗?如果有,是哪几对?问题讨论:
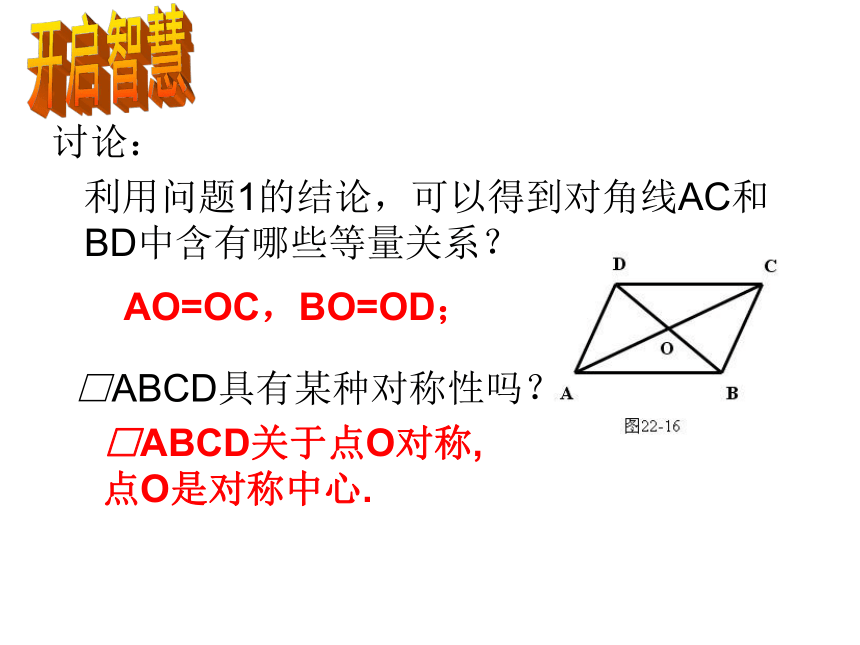
利用问题1的结论,可以得到对角线AC和BD中含有哪些等量关系?开启智慧□ABCD关于点O对称,点O是对称中心. □ABCD具有某种对称性吗?AO=OC,BO=OD;再看一遍看一看看一看平行四边形性质定理3:平行四边形的两条对角线互相平分.
平行四边形性质定理4:平行四边形是中心对称图形,对称中心是两条对角线的交点.归纳1、已知:如图(1),□ABCD中,AD=4cm,AC=10cm,BD=6cm,△AOD的周长是多少?练习提问:老人分地合理吗?12cm相等等底同高老大老二老三老四△AOD和△AOB的面积有什么关系?为什么?2、如图(2),在直角坐标平面内,□ABCD的对角线的交点正好与坐标原点重合.且点A、B的坐标分别为(3,2)、(-2,1).求点C、D的坐标.练习C(-3,-2)
D(2,-1)例题1
已知:如图22-17,□ABCD中,对角线AC、BD相交于点O,EF过点O且与边AB、CD分别相交于点E、F.
求证:OE=OF.例题讲解例题2
已知:如图22-18,□ABCD中,E、F分别是BC、AD上的点,且AE//CF.
求证:∠BAE=∠DCF.例题讲解3、如图(3),在□ABCD中,E为CD的中点, 联结BE并延长,交AD的延长线于点F,
求证:E是BF的中点,D是AF的中点. 练习边:两组对边分别平行且相等;
角:两组对角分别相等;
对角线:对角线互相平分;
对称性:平行四边形是中心对称图形,对称中心是两条对角线的交点. 小结你学到了什么?必做题:练习册习题22.2(2)
选做题:练习纸上的拓展练习1布置作业谢谢!ODBAC 如图,在□ABCD中,对角线AC、BD相交于点O,且AC+BD=20,△AOB的周长等于15,
则CD=______.5备用题 有没有这样的平行四边形,它的两条对角线长分别为14cm和20cm,它的一边长18cm?为什么? 备用题没有三角形的任意两边之和大于第三边. 如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________. 1<AD<9备用题 若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8D备用题三角形的任意两边之和大于第三边,任意两边之差小于第三边. 画一条直线,将下面备用图2的图形分成面积相等的两部分。备用题备用题
角:
推论:对边平行、对边相等对角相等夹在两条平行线间的平行线段相等l1l2温故(1)已知平行四边形两条邻边的比为2:5,周长为28cm,则这个平行四边形的四条边长分别为_____________________________.
(2)在□ABCD中,已知∠B+∠D=110°,则∠A=_____度,∠C=_____度.
4cm,10cm,4cm,10cm125125例题复习你来评一评 一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的: 老大老二老三老四 当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么? 1.平行四边形的两条对角线把这个平行四边形分为四个三角形.如图22-16,□ABCD的对角线AC和BD相交于点O,由AC和BD分□ABCD所得的四个三角形,有全等三角形吗?如果有,是哪几对?问题讨论:
利用问题1的结论,可以得到对角线AC和BD中含有哪些等量关系?开启智慧□ABCD关于点O对称,点O是对称中心. □ABCD具有某种对称性吗?AO=OC,BO=OD;再看一遍看一看看一看平行四边形性质定理3:平行四边形的两条对角线互相平分.
平行四边形性质定理4:平行四边形是中心对称图形,对称中心是两条对角线的交点.归纳1、已知:如图(1),□ABCD中,AD=4cm,AC=10cm,BD=6cm,△AOD的周长是多少?练习提问:老人分地合理吗?12cm相等等底同高老大老二老三老四△AOD和△AOB的面积有什么关系?为什么?2、如图(2),在直角坐标平面内,□ABCD的对角线的交点正好与坐标原点重合.且点A、B的坐标分别为(3,2)、(-2,1).求点C、D的坐标.练习C(-3,-2)
D(2,-1)例题1
已知:如图22-17,□ABCD中,对角线AC、BD相交于点O,EF过点O且与边AB、CD分别相交于点E、F.
求证:OE=OF.例题讲解例题2
已知:如图22-18,□ABCD中,E、F分别是BC、AD上的点,且AE//CF.
求证:∠BAE=∠DCF.例题讲解3、如图(3),在□ABCD中,E为CD的中点, 联结BE并延长,交AD的延长线于点F,
求证:E是BF的中点,D是AF的中点. 练习边:两组对边分别平行且相等;
角:两组对角分别相等;
对角线:对角线互相平分;
对称性:平行四边形是中心对称图形,对称中心是两条对角线的交点. 小结你学到了什么?必做题:练习册习题22.2(2)
选做题:练习纸上的拓展练习1布置作业谢谢!ODBAC 如图,在□ABCD中,对角线AC、BD相交于点O,且AC+BD=20,△AOB的周长等于15,
则CD=______.5备用题 有没有这样的平行四边形,它的两条对角线长分别为14cm和20cm,它的一边长18cm?为什么? 备用题没有三角形的任意两边之和大于第三边. 如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________. 1<AD<9备用题 若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8D备用题三角形的任意两边之和大于第三边,任意两边之差小于第三边. 画一条直线,将下面备用图2的图形分成面积相等的两部分。备用题备用题
