22.2(1)平行四边形的性质 课件(16张PPT)
文档属性
| 名称 | 22.2(1)平行四边形的性质 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 382.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览






文档简介
课件16张PPT。22.2(1) 平行四边形的性质
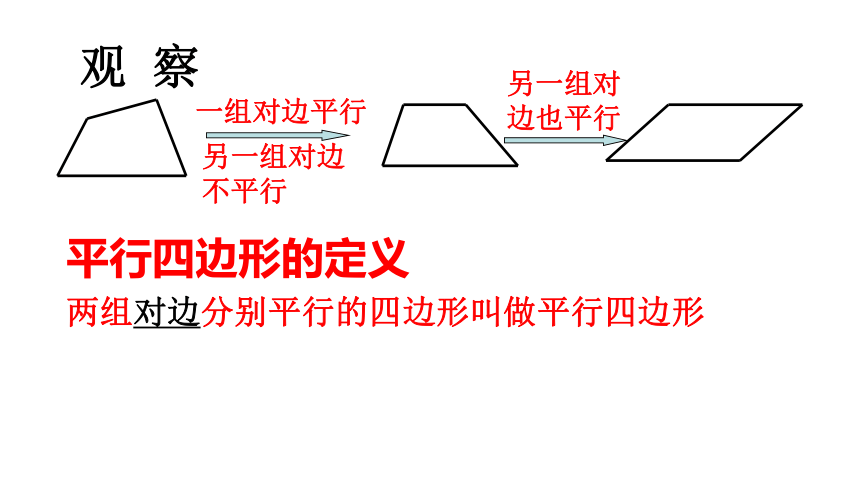
(第一课时)八年级数学第二学期这些图片中,含有你熟悉的图形吗?引入:(1)观察平行四边形的定义两组对边分别平行的四边形叫做平行四边形一组对边平行另一组对边
不平行另一组对边也平行观 察□ABCD你能指出□ABCD中的对边、对角、邻边、邻角吗? 引入:(2)概念平行四边形的表示:平行四边形用“ ”符号表示,记作□ABCD
平行四边形两组对边平行,除了平行还有什么
关系呢?那两组对角呢?对边相等对角相等已知:四边形ABCD为平行四边形
求证:AB=CD, AD=BC,
∠A= ∠C, ∠B= ∠D.猜想:论证:探究一:(1)思考、讨论平行四边形性质定理1:如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
(平行四边形对边相等)平行四边形性质定理2:如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
(平行四边形对角相等)探究一:(2)交流分析∵四边形ABCD是平行四边形
∴AD=BC ,AB=CD
(平行四边形对边相等)∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
(平行四边形对角相等)如图,如果 ∥ ,AB、CD垂直 ,那么AB与CD相等吗?为什么?
平行线间的距离处处相等 . ∵AB∥CD, AC∥BD,
∴四边形ABCD是平行四边形(平行四边形的定义),
∴ AB=CD(平行四边形的对边相等).夹在两条平行线间的平行线段相等. 探究二:
思考、讨论ACBDBDAC新知运用——例题例题1、小强用一根长度为36cm的铁丝围成了一个平行四边形的模型,其中一边长是8cm,其他三边的长分别是多少? 解:画平行四边形ABCD,设AB=8cm
∵四边形ABCD为平行四边形
∴ AD=BC ,AB=CD (平行四边形对边相等) ∵ AB+BC+CD+AD=36cm ,AB=8cm,
∴CD=8cm,2AD=20cm
∴AD=BC=10cm 答:其它三边的长分别是8cm,10cm,10cm. ∴ ∠A =∠ C,∠ B=∠ D ,(平行四边形对角相等), AD ∥BC(平行四边形定义),
∴∠A+∠B=180°.设∠A=x°,∠B=y°,又∠A比∠B大60°,则 ∴∠A=∠C=120°,∠B=∠D=60°.答:这个平行四边形各个内角度数分别为120°、120°、
60°、60°.
解: ∵四边形ABCD为平行四边形例题2、在□ABCD中,∠A比∠B大60°,求这个平行四边形各内角的度数?新知运用——例题(4) ABCD的周长为48,且AB = 2BC,
AB= ,BC= .(3)在 ABCD中,已知∠A+∠C=200°,
则∠A= ,∠B= .巩固训练(1) 在 ABCD中,已知∠A=50°,则∠B= ,∠C= ,∠D= .50°130°130°16100°80°X2X816(2) 在 ABCD中,AB=3,BC=5,则 ABCD的周长为 .在△AED和△CFB中,
∠1=∠2,
∠3=∠4,
AD=BC,
∴ △AED≌△CFB(A.A .S).
∴AE=CF.已知:如图,□ ABCD中,AE⊥BD,CF⊥BD,
垂足分别为点E、F. 求证:AE=CF.证明: ∵四边形ABCD是平行四边形
∴AD=BC (平行四边形对边相等)
AD∥BC (平行四边形的定义)
∴∠1=∠2,
又∵AE⊥BD,CF⊥BD,
∴∠3=∠4=90°,
提高
训练提升训练已知:如图,□ ABCD中,∠ADC的平分线与AB相交于点E.
求证:BE+BC=CD.平行四边形的性质课堂小结:今天我们学了几个知识点?拓展如图,已知一个四边形是以点A, B, C, D为顶点的平行四边形,其坐标分别为A (0,0),
B (5,0), D (3,3).
(1)画出所有满足条件的平行四边形;
(2)写出顶点C的坐标为__________. xyA(0,0)D(3,3)B(5,0)课后作业练习册:22.2(1)
谢谢大家!感谢各位领导和老师的指导
(第一课时)八年级数学第二学期这些图片中,含有你熟悉的图形吗?引入:(1)观察平行四边形的定义两组对边分别平行的四边形叫做平行四边形一组对边平行另一组对边
不平行另一组对边也平行观 察□ABCD你能指出□ABCD中的对边、对角、邻边、邻角吗? 引入:(2)概念平行四边形的表示:平行四边形用“ ”符号表示,记作□ABCD
平行四边形两组对边平行,除了平行还有什么
关系呢?那两组对角呢?对边相等对角相等已知:四边形ABCD为平行四边形
求证:AB=CD, AD=BC,
∠A= ∠C, ∠B= ∠D.猜想:论证:探究一:(1)思考、讨论平行四边形性质定理1:如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
(平行四边形对边相等)平行四边形性质定理2:如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
(平行四边形对角相等)探究一:(2)交流分析∵四边形ABCD是平行四边形
∴AD=BC ,AB=CD
(平行四边形对边相等)∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
(平行四边形对角相等)如图,如果 ∥ ,AB、CD垂直 ,那么AB与CD相等吗?为什么?
平行线间的距离处处相等 . ∵AB∥CD, AC∥BD,
∴四边形ABCD是平行四边形(平行四边形的定义),
∴ AB=CD(平行四边形的对边相等).夹在两条平行线间的平行线段相等. 探究二:
思考、讨论ACBDBDAC新知运用——例题例题1、小强用一根长度为36cm的铁丝围成了一个平行四边形的模型,其中一边长是8cm,其他三边的长分别是多少? 解:画平行四边形ABCD,设AB=8cm
∵四边形ABCD为平行四边形
∴ AD=BC ,AB=CD (平行四边形对边相等) ∵ AB+BC+CD+AD=36cm ,AB=8cm,
∴CD=8cm,2AD=20cm
∴AD=BC=10cm 答:其它三边的长分别是8cm,10cm,10cm. ∴ ∠A =∠ C,∠ B=∠ D ,(平行四边形对角相等), AD ∥BC(平行四边形定义),
∴∠A+∠B=180°.设∠A=x°,∠B=y°,又∠A比∠B大60°,则 ∴∠A=∠C=120°,∠B=∠D=60°.答:这个平行四边形各个内角度数分别为120°、120°、
60°、60°.
解: ∵四边形ABCD为平行四边形例题2、在□ABCD中,∠A比∠B大60°,求这个平行四边形各内角的度数?新知运用——例题(4) ABCD的周长为48,且AB = 2BC,
AB= ,BC= .(3)在 ABCD中,已知∠A+∠C=200°,
则∠A= ,∠B= .巩固训练(1) 在 ABCD中,已知∠A=50°,则∠B= ,∠C= ,∠D= .50°130°130°16100°80°X2X816(2) 在 ABCD中,AB=3,BC=5,则 ABCD的周长为 .在△AED和△CFB中,
∠1=∠2,
∠3=∠4,
AD=BC,
∴ △AED≌△CFB(A.A .S).
∴AE=CF.已知:如图,□ ABCD中,AE⊥BD,CF⊥BD,
垂足分别为点E、F. 求证:AE=CF.证明: ∵四边形ABCD是平行四边形
∴AD=BC (平行四边形对边相等)
AD∥BC (平行四边形的定义)
∴∠1=∠2,
又∵AE⊥BD,CF⊥BD,
∴∠3=∠4=90°,
提高
训练提升训练已知:如图,□ ABCD中,∠ADC的平分线与AB相交于点E.
求证:BE+BC=CD.平行四边形的性质课堂小结:今天我们学了几个知识点?拓展如图,已知一个四边形是以点A, B, C, D为顶点的平行四边形,其坐标分别为A (0,0),
B (5,0), D (3,3).
(1)画出所有满足条件的平行四边形;
(2)写出顶点C的坐标为__________. xyA(0,0)D(3,3)B(5,0)课后作业练习册:22.2(1)
谢谢大家!感谢各位领导和老师的指导
