22.3(5)特殊的平行四边形 课件(17张PPT)
文档属性
| 名称 | 22.3(5)特殊的平行四边形 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 91.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览



文档简介
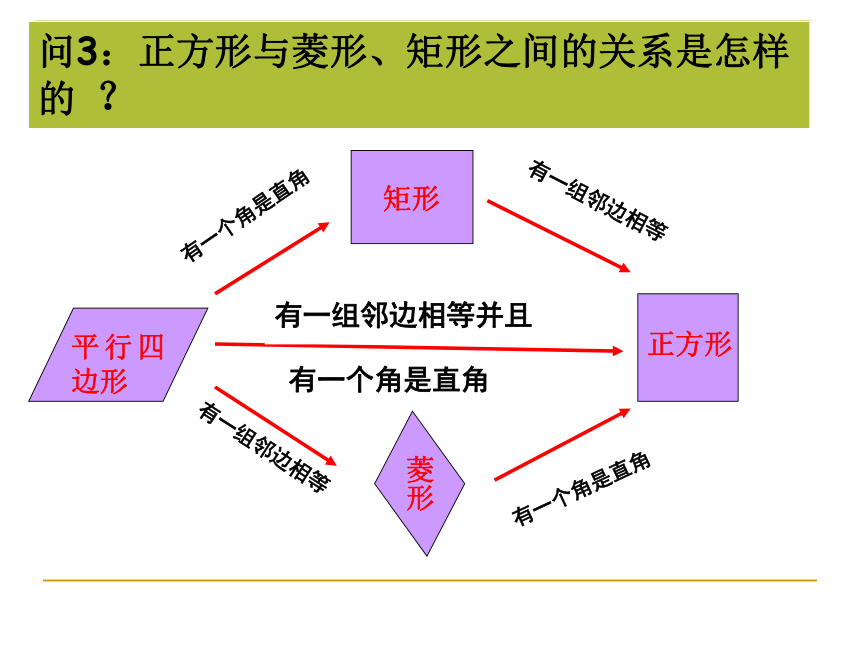
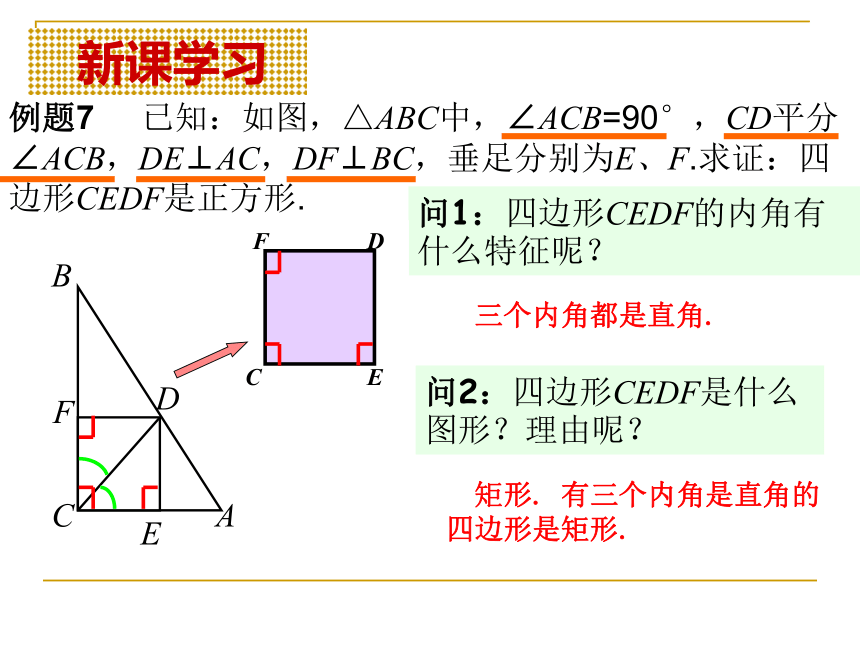
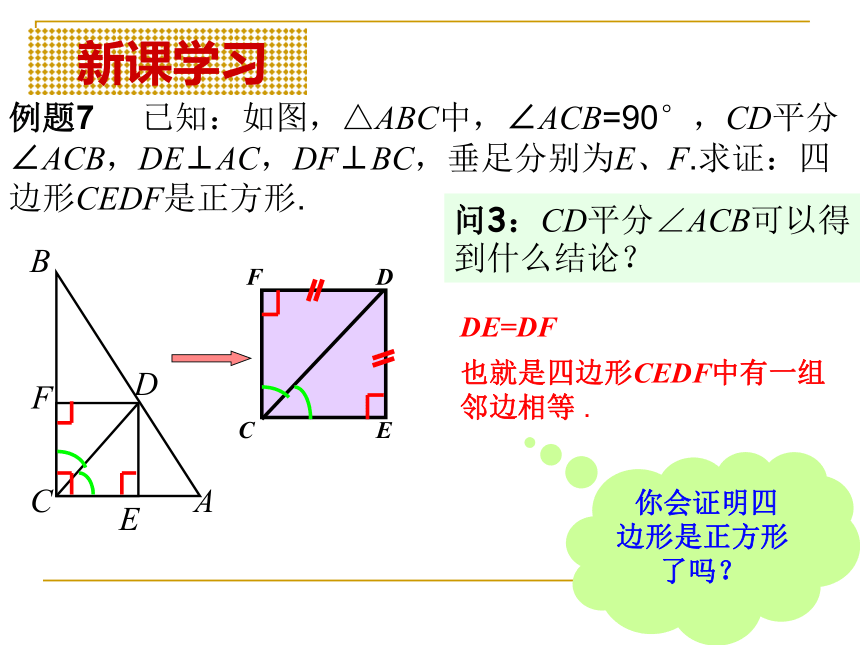
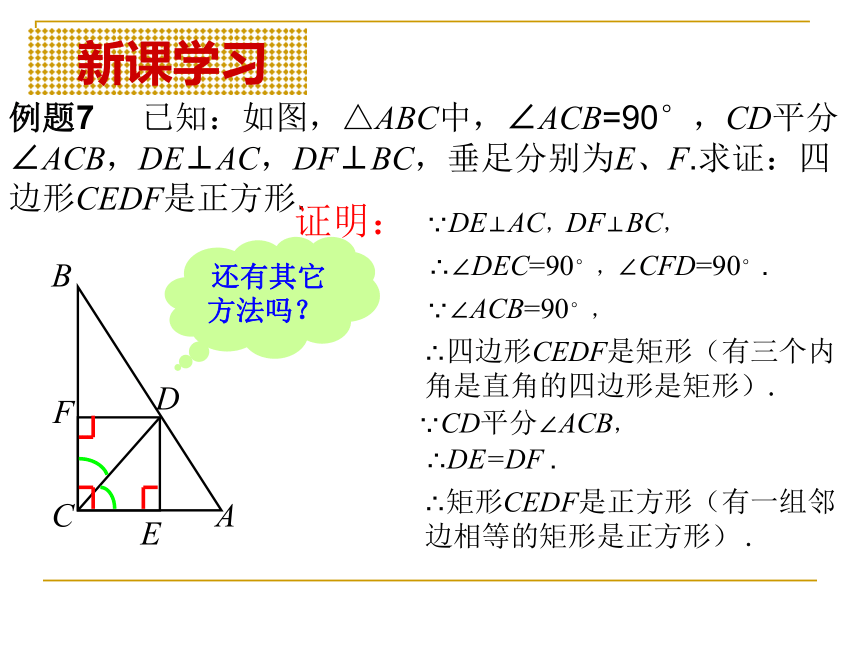
课件17张PPT。§22.3特殊的平行四边形(5) 复习引入问1:什么是正方形 ?有一组_____相等并且有一个内角是_______的__________形叫做正方形. 问2:正方形的判定定理是什么 ?邻边直角平行四边判定定理1:有一组邻边相等的矩形是正方形.判定定理2:有一个内角是直角的菱形是正方形. 问3:正方形与菱形、矩形之间的关系是怎样的 ?平行四边形有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角平行四边形菱形矩形正方形如果用集合的思想可以怎样表示? 复习引入 新课学习例题7 已知:如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC,DF⊥BC,垂足分别为E、F.求证:四边形CEDF是正方形.问1:四边形CEDF的内角有什么特征呢? 三个内角都是直角.问2:四边形CEDF是什么图形?理由呢? 矩形. 有三个内角是直角的四边形是矩形. 新课学习例题7 已知:如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC,DF⊥BC,垂足分别为E、F.求证:四边形CEDF是正方形.问3:CD平分∠ACB可以得到什么结论? DE=DF 也就是四边形CEDF中有一组邻边相等 . 你会证明四边形是正方形了吗? 新课学习例题7 已知:如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC,DF⊥BC,垂足分别为E、F.求证:四边形CEDF是正方形.证明:∵DE⊥AC,DF⊥BC,∴∠DEC=90°,∠CFD=90°. ∴DE=DF . ∴四边形CEDF是矩形(有三个内角是直角的四边形是矩形).∵∠ACB=90°, ∵CD平分∠ACB, ∴矩形CEDF是正方形(有一组邻边相等的矩形是正方形) . 还有其它方法吗? 新课学习方法2证明: ∵∠ACB=90°,
∴菱形CEDF是正方形(有一个角是直角的菱形是正方形).小结:要判定一个四边形是正方形,根据定义,通常只要判定四边形既是矩形又是菱形。∵∠ACB=90°
∴BC⊥AC,
∵DE⊥AC,
∴DE∥FC.
同理可得CE∥FD.
∴四边形CEDF是平行四边形 (平行四边形的定义). ∵CD平分∠ACB, DE⊥AC, DF⊥BC,
∴DE=DF.
∴四边形CEDF是菱形(有一组邻边相等的平行四边形是菱形).
新课学习例题8 已知:如图,矩形ABCD的四个内角的平分线组成四边形EFGH.
求证:四边形EFGH是正方形.DCBAHFGECF问1:直角的角平分线会分成多少度的角? 45°的角. 问2:矩形ABCD的相邻两个内角∠DAB、∠ABC的平分线相交成什么角? 90°的角. ∠5=90°. 新课学习例题8 已知:如图,矩形ABCD的四个内角的平分线组成四边形EFGH.
求证:四边形EFGH是正方形.DCBAHFGECF问3:根据已知条件还可以得到四边形EFGH中哪些角的度数是90°? ∠H =∠F =∠FGH=90° . 问4: 如何证明四边形EFGH是正方形 ? 证明四边形EFGH是矩形,再证明它有一组邻边相等 . 新课学习例题8 已知:如图,矩形ABCD的四个内角的平分线组成四边形EFGH.
求证:四边形EFGH是正方形.DCBAHFGECF问5:如何证明EF=EH? 由分解图形可证全等三角形,得 AF = BH,再由等角对等边得AE = BE.证明:∵ 四边形ABCD是矩形,
∴∠DAB = ∠ABC = 90°(矩形的四个角都是直角).
又∵AF、BH、CH、DF是四个内角的平分线,
∴∠1 = ∠2 = ∠DAB=45°,
∠3 = ∠4 = ∠ABC=45°,
∴∠AEB = ∠HEF = 90°.
同理,可得∠H = ∠F = 90°.
∴ 四边形EFGH是矩形(有三个角是直角的四边形是矩形).
新课学习DCBAHFGECF∵∠2 = ∠4, AD = BC,
∴Rt△ADF ≌ Rt△BCH,
∴ AF = BH.
∵∠1 = ∠3
∴AE = BE.
∴AF-AE = BH-BE, 即EH = EF.
∴矩形EFGH是正方形(有一组邻边相等的矩形是正方形). 课堂练习练习1 如图,P是正方形ABCD内一点,将△ABP绕 点B顺时针方向选择后与△CBP重合,若PB=3,则
PP’= ______.CDP’PBA 通过图形的运动将一些分散的元素集中,得到△B PP’是等腰直角三角形. 课堂练习练习2 有下列图形:(1)平行四边形(非矩形、菱形) (2)矩形(邻边不等)(3)菱形(内角不等于直角)(4)正方形.其中,
中心对称图形有___________________(填写图形前 的序号,下同);
轴对称图形有_________________;
对角线互相垂直平分且相等的有_________________.(1)(2)(3)(4) (2)(3)(4) (4) 课堂练习练习3 已知:如图,在正方形ABCD中,E为BC延长线上的一点,F是CD上的一点,且CF=CE,BF的延长线交DE于点G.求证:BF⊥DE.AGECBDF问1:由已知条件正方形ABCD可以得到哪些结论?问2:图中有什么基本图形? 问3:证明全等三角形的目的是什么 ? 课堂小结 谈谈这节课你有什么收获、体会或想法? (1)特殊的平行四边形的性质、判定的综合运用.将复杂图形中的基本图形分解出来,找出已知、求证所需要的条件 .布置作业 练习册:习题22.3(5)
∴菱形CEDF是正方形(有一个角是直角的菱形是正方形).小结:要判定一个四边形是正方形,根据定义,通常只要判定四边形既是矩形又是菱形。∵∠ACB=90°
∴BC⊥AC,
∵DE⊥AC,
∴DE∥FC.
同理可得CE∥FD.
∴四边形CEDF是平行四边形 (平行四边形的定义). ∵CD平分∠ACB, DE⊥AC, DF⊥BC,
∴DE=DF.
∴四边形CEDF是菱形(有一组邻边相等的平行四边形是菱形).
新课学习例题8 已知:如图,矩形ABCD的四个内角的平分线组成四边形EFGH.
求证:四边形EFGH是正方形.DCBAHFGECF问1:直角的角平分线会分成多少度的角? 45°的角. 问2:矩形ABCD的相邻两个内角∠DAB、∠ABC的平分线相交成什么角? 90°的角. ∠5=90°. 新课学习例题8 已知:如图,矩形ABCD的四个内角的平分线组成四边形EFGH.
求证:四边形EFGH是正方形.DCBAHFGECF问3:根据已知条件还可以得到四边形EFGH中哪些角的度数是90°? ∠H =∠F =∠FGH=90° . 问4: 如何证明四边形EFGH是正方形 ? 证明四边形EFGH是矩形,再证明它有一组邻边相等 . 新课学习例题8 已知:如图,矩形ABCD的四个内角的平分线组成四边形EFGH.
求证:四边形EFGH是正方形.DCBAHFGECF问5:如何证明EF=EH? 由分解图形可证全等三角形,得 AF = BH,再由等角对等边得AE = BE.证明:∵ 四边形ABCD是矩形,
∴∠DAB = ∠ABC = 90°(矩形的四个角都是直角).
又∵AF、BH、CH、DF是四个内角的平分线,
∴∠1 = ∠2 = ∠DAB=45°,
∠3 = ∠4 = ∠ABC=45°,
∴∠AEB = ∠HEF = 90°.
同理,可得∠H = ∠F = 90°.
∴ 四边形EFGH是矩形(有三个角是直角的四边形是矩形).
新课学习DCBAHFGECF∵∠2 = ∠4, AD = BC,
∴Rt△ADF ≌ Rt△BCH,
∴ AF = BH.
∵∠1 = ∠3
∴AE = BE.
∴AF-AE = BH-BE, 即EH = EF.
∴矩形EFGH是正方形(有一组邻边相等的矩形是正方形). 课堂练习练习1 如图,P是正方形ABCD内一点,将△ABP绕 点B顺时针方向选择后与△CBP重合,若PB=3,则
PP’= ______.CDP’PBA 通过图形的运动将一些分散的元素集中,得到△B PP’是等腰直角三角形. 课堂练习练习2 有下列图形:(1)平行四边形(非矩形、菱形) (2)矩形(邻边不等)(3)菱形(内角不等于直角)(4)正方形.其中,
中心对称图形有___________________(填写图形前 的序号,下同);
轴对称图形有_________________;
对角线互相垂直平分且相等的有_________________.(1)(2)(3)(4) (2)(3)(4) (4) 课堂练习练习3 已知:如图,在正方形ABCD中,E为BC延长线上的一点,F是CD上的一点,且CF=CE,BF的延长线交DE于点G.求证:BF⊥DE.AGECBDF问1:由已知条件正方形ABCD可以得到哪些结论?问2:图中有什么基本图形? 问3:证明全等三角形的目的是什么 ? 课堂小结 谈谈这节课你有什么收获、体会或想法? (1)特殊的平行四边形的性质、判定的综合运用.将复杂图形中的基本图形分解出来,找出已知、求证所需要的条件 .布置作业 练习册:习题22.3(5)
