22.3 特殊的平行四边形——矩形、菱形的判定 课件(19张PPT)
文档属性
| 名称 | 22.3 特殊的平行四边形——矩形、菱形的判定 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 16:08:39 | ||
图片预览



文档简介
课件19张PPT。§22.3 特殊的平行四边形(3)矩形、菱形的判定探求新知思考:
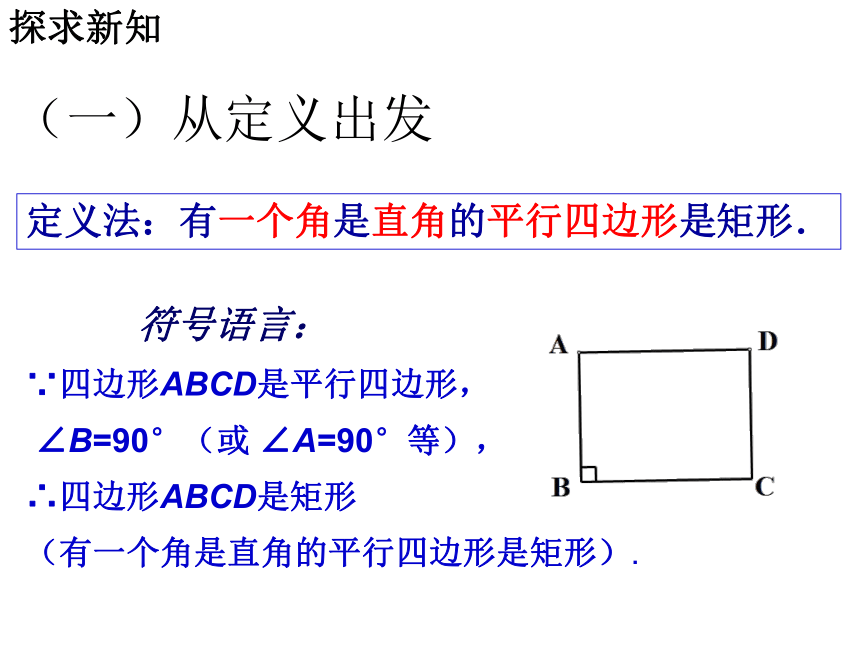
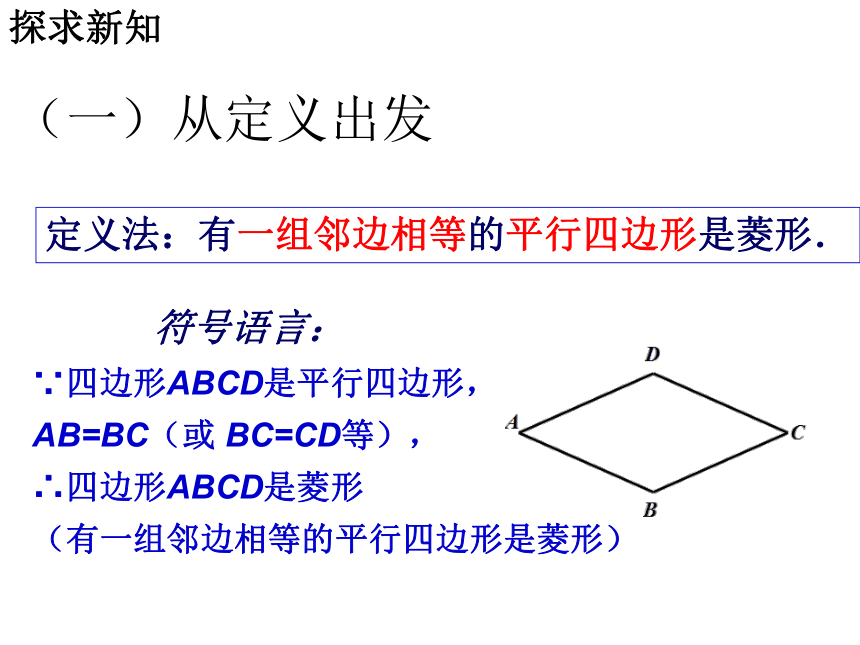
如何从矩形、菱形特殊的性质出发,得出矩形、菱形的判定? (一)从定义出发(三)从四边形对角线出发(二)从四边形的边或角出发探求新知(一)从定义出发定义法:有一个角是直角的平行四边形是矩形.定义法:有一组邻边相等的平行四边形是菱形. 符号语言:
∵四边形ABCD是平行四边形,
∠B=90°(或 ∠A=90°等),
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形).探求新知(一)从定义出发定义法:有一个角是直角的平行四边形是矩形.探求新知 符号语言:
∵四边形ABCD是平行四边形,
AB=BC(或 BC=CD等),
∴四边形ABCD是菱形
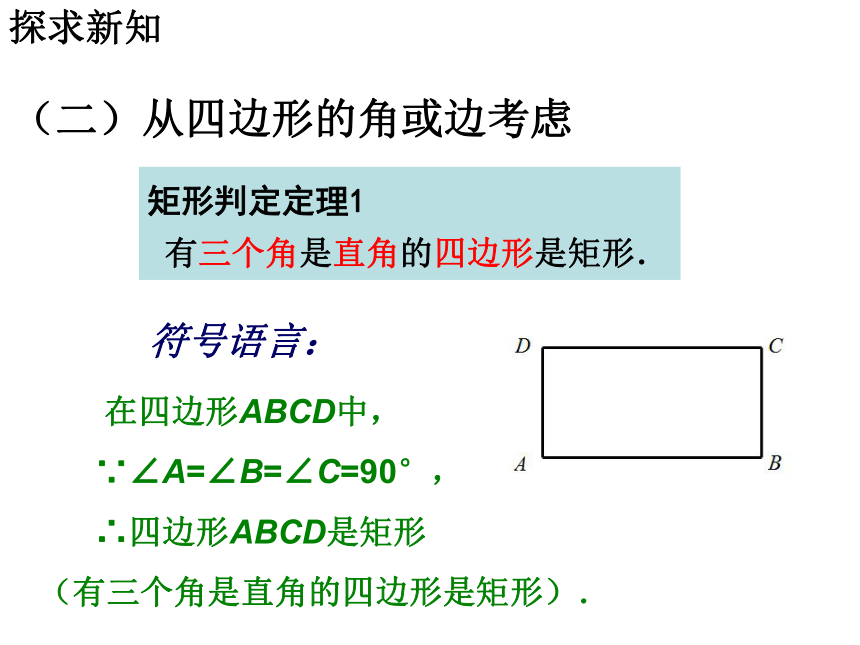
(有一组邻边相等的平行四边形是菱形)(一)从定义出发定义法:有一组邻边相等的平行四边形是菱形.(二)从四边形的角或边考虑矩形判定定理1
有三个角是直角的四边形是矩形.探求新知 符号语言: 在四边形ABCD中,
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形
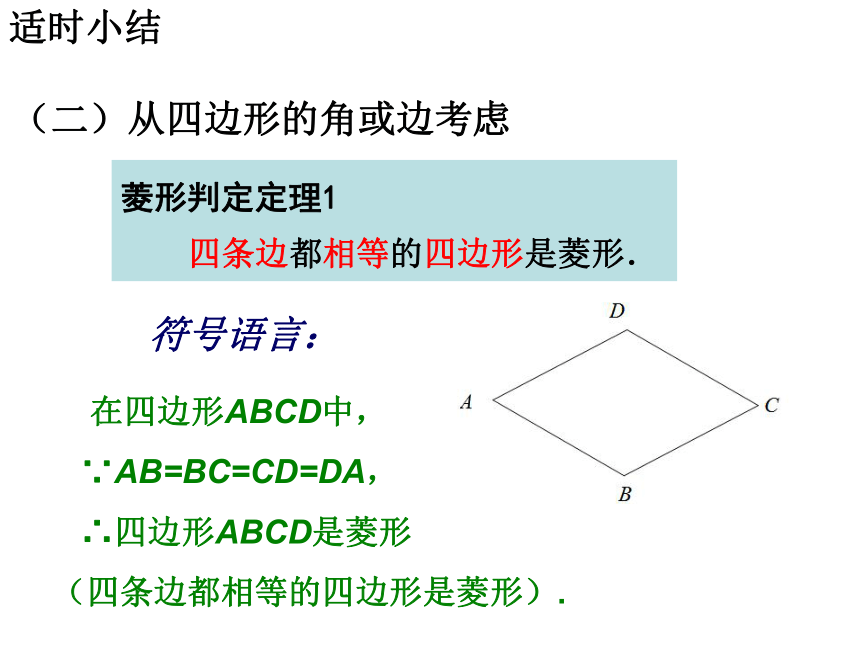
(有三个角是直角的四边形是矩形).(二)从四边形的角或边考虑菱形判定定理1
四条边都相等的四边形是菱形.适时小结 符号语言: 在四边形ABCD中,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形
(四条边都相等的四边形是菱形).已知:在平行四边形ABCD中,AC=BD.
求证:四边形ABCD是矩形.探求新知(三)从平行四边形的对角线出发(三)从平行四边形的对角线出发 矩形判定定理2
对角线相等的平行四边形是矩形. 符号语言:
∵四边形ABCD是平行四边形,
AC=BD,
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形).探求新知已知:在平行四边形ABCD中,AC⊥BD.
求证:四边形ABCD是菱形.探求新知(三)从平行四边形的对角线出发 菱形判定定理2
对角线互相垂直的平行四边形是菱形. 符号语言:
∵四边形ABCD是平行四边形,
AC⊥BD,
∴四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)探求新知(三)从平行四边形的对角线出发有三个角是直角的四边形是矩形对角线相等的平行四边形是矩形定义法:
有一个角是直角的平行四边形是矩形四条边都相等的四边形是菱形.对角线互相垂直的平行四边形是菱形.定义法:
有一组邻边相等的平行四边形是菱形.性质和判定定理的综合运用例题 :如图:矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别在AO、BO、CO、DO上,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
例题5 已知如图:EF是□ABCD的对角线AC的垂直平分线,
EF与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.性质和判定定理的综合运用对边平行,即AD∥BC分析: 问1:由条件“□ABCD”可得怎样的结论?∠1=∠212 问2:由条件“EF是对角线AC的垂直平分线”可得怎样的结论?OA=OC 34 问3:可得哪两个三角形全等?△AOE≌△COFOE=OFOA=OC□AFCEAC⊥EFAFCE是菱形.∠3=∠4=∴AE∥FC(平行四边形的对边平行)
∴∠1=∠2,
∵EF垂直平分AC,
∴AO=CO, ∠3=∠4=90°.
∵在△AOE和△COF中,
∴ △ AOE≌ △ COF(A.S.A),∴EO=FO.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形). 又∵EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形)。例题5 已知如图:EF是□ ABCD的对角线AC的垂直平分线,EF与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.性质和判定定理的综合运用∵四边形ABCD是平行四边形,证明:1234如图:已知BF、BE分别是∠ABC与它的邻补角∠ABD的角平分线,AE⊥BE于点E,AF⊥BF于点F,那么四边形AEBF是矩形吗?为什么?
问:分析本题的关键是什么?课堂练习答:四边形AEBF是矩形.
证明: ∵BF、BE分别是∠ABC与∠ABD的角平分线,
∴∠1= ∠ABC,同理 ∠2= ∠ABD,
∴∠1+∠2= ∠ABC+ ∠ABD= (∠ABC+∠ABD)= ×180°=90°,
即∠EBF=90°,
∵AE⊥BE,AF⊥BF,
∴∠AEB=∠AFB=90°,
∴∠EBF=∠AEB=∠AFB=90°,
∴四边形AEBF是矩形(有三个角是直角的四边形是矩形).由题中 两个垂直条件可知:四边形中有两个直角,只需再证得一个角是直角即可.四边形平行四边形矩形和菱形的判定方法课堂小结练习册:第43页 习题22.3(3)布置作业
如何从矩形、菱形特殊的性质出发,得出矩形、菱形的判定? (一)从定义出发(三)从四边形对角线出发(二)从四边形的边或角出发探求新知(一)从定义出发定义法:有一个角是直角的平行四边形是矩形.定义法:有一组邻边相等的平行四边形是菱形. 符号语言:
∵四边形ABCD是平行四边形,
∠B=90°(或 ∠A=90°等),
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形).探求新知(一)从定义出发定义法:有一个角是直角的平行四边形是矩形.探求新知 符号语言:
∵四边形ABCD是平行四边形,
AB=BC(或 BC=CD等),
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形是菱形)(一)从定义出发定义法:有一组邻边相等的平行四边形是菱形.(二)从四边形的角或边考虑矩形判定定理1
有三个角是直角的四边形是矩形.探求新知 符号语言: 在四边形ABCD中,
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形
(有三个角是直角的四边形是矩形).(二)从四边形的角或边考虑菱形判定定理1
四条边都相等的四边形是菱形.适时小结 符号语言: 在四边形ABCD中,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形
(四条边都相等的四边形是菱形).已知:在平行四边形ABCD中,AC=BD.
求证:四边形ABCD是矩形.探求新知(三)从平行四边形的对角线出发(三)从平行四边形的对角线出发 矩形判定定理2
对角线相等的平行四边形是矩形. 符号语言:
∵四边形ABCD是平行四边形,
AC=BD,
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形).探求新知已知:在平行四边形ABCD中,AC⊥BD.
求证:四边形ABCD是菱形.探求新知(三)从平行四边形的对角线出发 菱形判定定理2
对角线互相垂直的平行四边形是菱形. 符号语言:
∵四边形ABCD是平行四边形,
AC⊥BD,
∴四边形ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)探求新知(三)从平行四边形的对角线出发有三个角是直角的四边形是矩形对角线相等的平行四边形是矩形定义法:
有一个角是直角的平行四边形是矩形四条边都相等的四边形是菱形.对角线互相垂直的平行四边形是菱形.定义法:
有一组邻边相等的平行四边形是菱形.性质和判定定理的综合运用例题 :如图:矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别在AO、BO、CO、DO上,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
例题5 已知如图:EF是□ABCD的对角线AC的垂直平分线,
EF与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.性质和判定定理的综合运用对边平行,即AD∥BC分析: 问1:由条件“□ABCD”可得怎样的结论?∠1=∠212 问2:由条件“EF是对角线AC的垂直平分线”可得怎样的结论?OA=OC 34 问3:可得哪两个三角形全等?△AOE≌△COFOE=OFOA=OC□AFCEAC⊥EFAFCE是菱形.∠3=∠4=∴AE∥FC(平行四边形的对边平行)
∴∠1=∠2,
∵EF垂直平分AC,
∴AO=CO, ∠3=∠4=90°.
∵在△AOE和△COF中,
∴ △ AOE≌ △ COF(A.S.A),∴EO=FO.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形). 又∵EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形)。例题5 已知如图:EF是□ ABCD的对角线AC的垂直平分线,EF与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.性质和判定定理的综合运用∵四边形ABCD是平行四边形,证明:1234如图:已知BF、BE分别是∠ABC与它的邻补角∠ABD的角平分线,AE⊥BE于点E,AF⊥BF于点F,那么四边形AEBF是矩形吗?为什么?
问:分析本题的关键是什么?课堂练习答:四边形AEBF是矩形.
证明: ∵BF、BE分别是∠ABC与∠ABD的角平分线,
∴∠1= ∠ABC,同理 ∠2= ∠ABD,
∴∠1+∠2= ∠ABC+ ∠ABD= (∠ABC+∠ABD)= ×180°=90°,
即∠EBF=90°,
∵AE⊥BE,AF⊥BF,
∴∠AEB=∠AFB=90°,
∴∠EBF=∠AEB=∠AFB=90°,
∴四边形AEBF是矩形(有三个角是直角的四边形是矩形).由题中 两个垂直条件可知:四边形中有两个直角,只需再证得一个角是直角即可.四边形平行四边形矩形和菱形的判定方法课堂小结练习册:第43页 习题22.3(3)布置作业
