22.2(3)平行四边形的判定 复习课件(24张PPT)
文档属性
| 名称 | 22.2(3)平行四边形的判定 复习课件(24张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 469.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览



文档简介
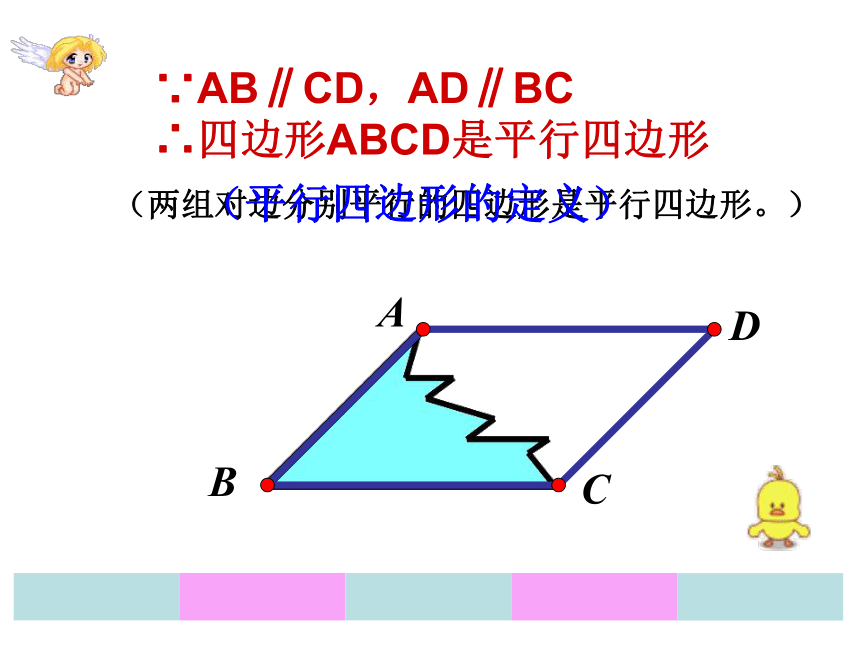
课件24张PPT。 这是平行四边形玻璃的一部分,它打碎后正好保留了一个角和两条邻边。你能帮切割玻璃的师傅找回它原来的形状大小,以便重新切割一块吗?ACBADCB∵AB∥CD,AD∥BC
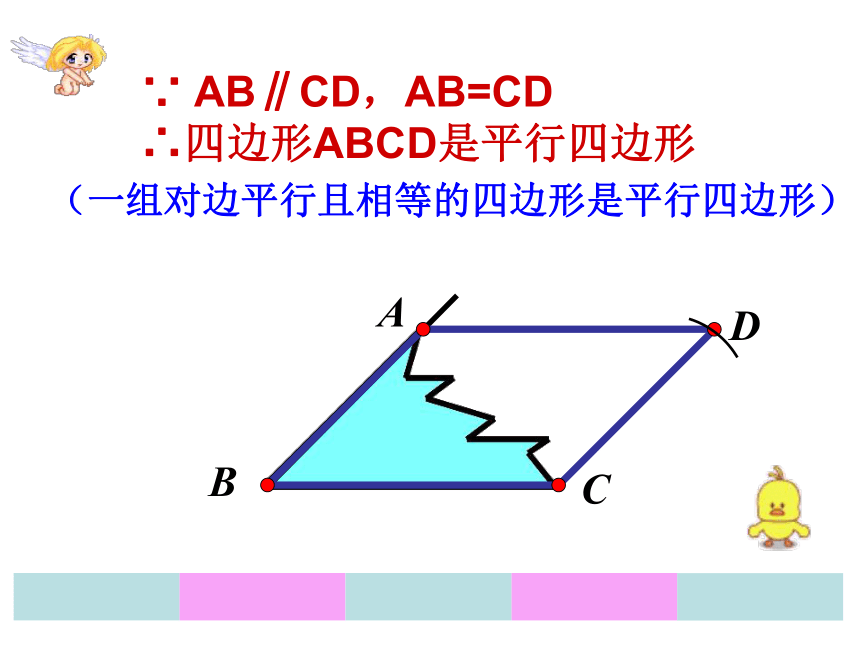
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形。)(平行四边形的定义)ADCB∵ AB∥CD,AB=CD
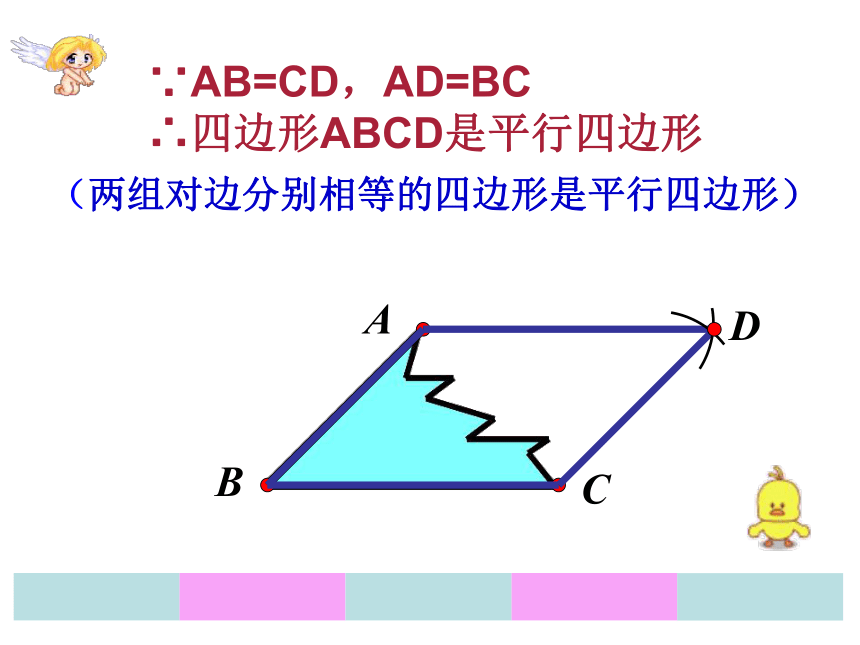
∴四边形ABCD是平行四边形 (一组对边平行且相等的四边形是平行四边形)ACBD∵AB=CD,AD=BC
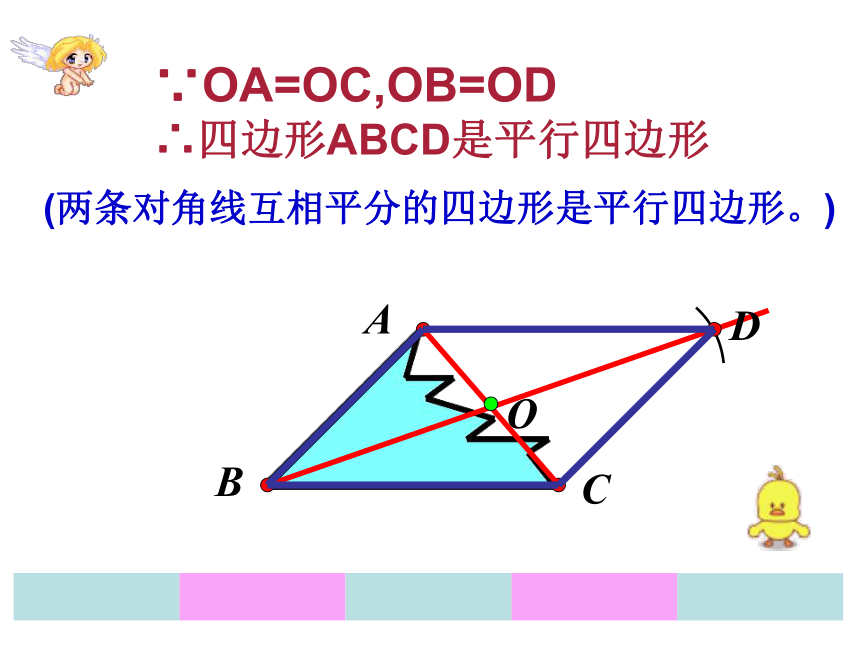
∴四边形ABCD是平行四边形 (两组对边分别相等的四边形是平行四边形)ACBDO∵OA=OC,OB=OD
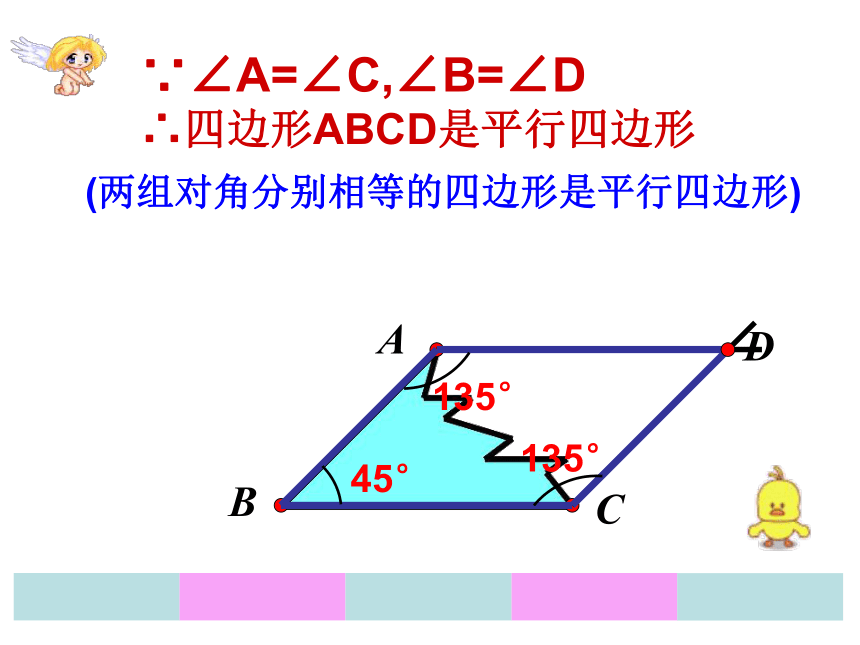
∴四边形ABCD是平行四边形 (两条对角线互相平分的四边形是平行四边形。) ACBD45°135°135°∵∠A=∠C,∠B=∠D
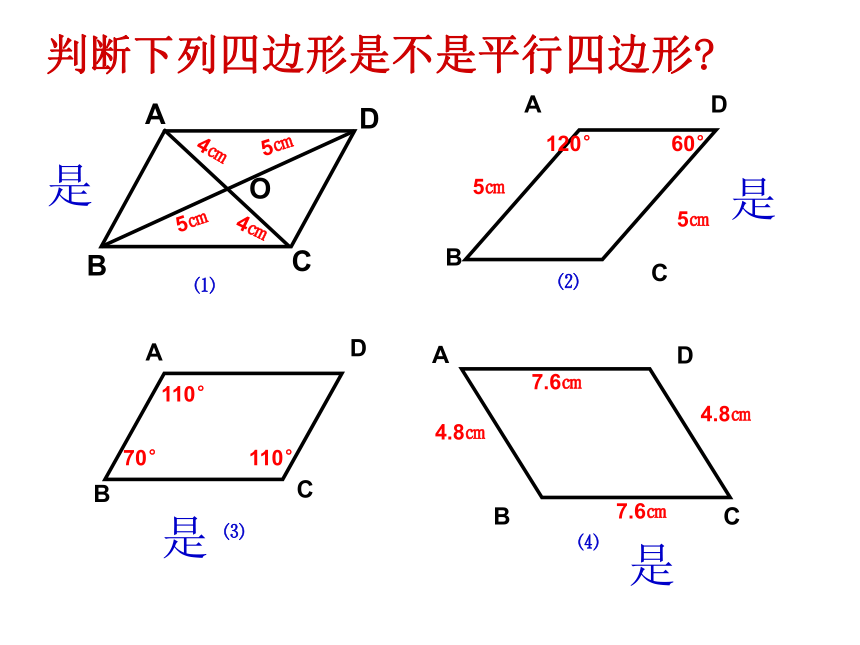
∴四边形ABCD是平行四边形 (两组对角分别相等的四边形是平行四边形)平行四边形的判定(复习)定义:两组对边分别平行的四边形是平行四边形.定理1:两组对边分别相等的四边形是平行四边形.定理2:一组对边平行且相等的四边形是平行四边形.定理3:对角线互相平分的四边形是平行四边形.定理4:两组对角分别相等的四边形是平行四边形.平行四边形的判定判断下列四边形是不是平行四边形?AD是是是是练习1:如图:AB=CD,且∠1=∠2,
四边形ABCD是平行四边形吗?12已知:如图,在□ABCD中,AE平分∠BAD,交DC的延长线于点E,CF平分∠BCD,交BA的延长线于点F.
求证:四边形AECF是平行四边形.
练习2:1234GH练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EF练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EFDE∥BF练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EF∠1=∠212练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EF∠1=∠212练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,条件___________________,使四边形BFDE是平行四边形。EFBE⊥AC于E,DF⊥AC于F∵四边形ABCD是平行四边形 DBCAEF∴AO=CO , BO=DO (平行四边形对角线互相平分) ∵AE=CF EO=AO?AE
FO=CO?CF O∴EO=FO 又∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分的四边形是平行四边形) 证明: 联结BD,与AC交于点O添条件:AE=CF 有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。对角线相等的四边形是平行四边形。一条对角线平分另一条对角线的四
边形是平行四边形。判断题筝形两组对边分别相等的四边形是平行四边形。有一组对边平行,另外一组对边相等的四边形一定是平行四边形。 紧扣定理作业:补充题 由因索果 合理推理 言必有据ACBDO高度攀一攀在四边形ABCD中,对角线AC、BD相交于点O。给出五个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC.
从以上条件中任取两个,能判断四边形ABCD是平行四边形的有______________________________;不能判断的有____________________(并举出反例)。①和②;①和③;①和④;①和⑤;②和⑤;④和⑤②和③;②和④;③和④;③和⑤;示意图高度攀一攀②OA=OC;③AB=CD;ACBDO高度攀一攀②OA=OC;④∠BAD=∠DCBACBDO筝形高度攀一攀③AB=CD;④∠BAD=∠DCBACBDABCD高度攀一攀③AB=CD;⑤AD ∥BC.ACBD
四边形ABCD是平行四边形吗?12已知:如图,在□ABCD中,AE平分∠BAD,交DC的延长线于点E,CF平分∠BCD,交BA的延长线于点F.
求证:四边形AECF是平行四边形.
练习2:1234GH练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EF练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EFDE∥BF练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EF∠1=∠212练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,请加一个条件_______,使四边形BFDE是平行四边形。EF∠1=∠212练习3:如图,在□ABCD中,点E、F是对角线AC上的两点,条件___________________,使四边形BFDE是平行四边形。EFBE⊥AC于E,DF⊥AC于F∵四边形ABCD是平行四边形 DBCAEF∴AO=CO , BO=DO (平行四边形对角线互相平分) ∵AE=CF EO=AO?AE
FO=CO?CF O∴EO=FO 又∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分的四边形是平行四边形) 证明: 联结BD,与AC交于点O添条件:AE=CF 有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。对角线相等的四边形是平行四边形。一条对角线平分另一条对角线的四
边形是平行四边形。判断题筝形两组对边分别相等的四边形是平行四边形。有一组对边平行,另外一组对边相等的四边形一定是平行四边形。 紧扣定理作业:补充题 由因索果 合理推理 言必有据ACBDO高度攀一攀在四边形ABCD中,对角线AC、BD相交于点O。给出五个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC.
从以上条件中任取两个,能判断四边形ABCD是平行四边形的有______________________________;不能判断的有____________________(并举出反例)。①和②;①和③;①和④;①和⑤;②和⑤;④和⑤②和③;②和④;③和④;③和⑤;示意图高度攀一攀②OA=OC;③AB=CD;ACBDO高度攀一攀②OA=OC;④∠BAD=∠DCBACBDO筝形高度攀一攀③AB=CD;④∠BAD=∠DCBACBDABCD高度攀一攀③AB=CD;⑤AD ∥BC.ACBD
