22.2(1)平行四边形的性质 课件(19张PPT)
文档属性
| 名称 | 22.2(1)平行四边形的性质 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 00:00:00 | ||
图片预览



文档简介
课件19张PPT。八年级第二学期数学22.2(1) 平行四边形
——平行四边形的性质(1)
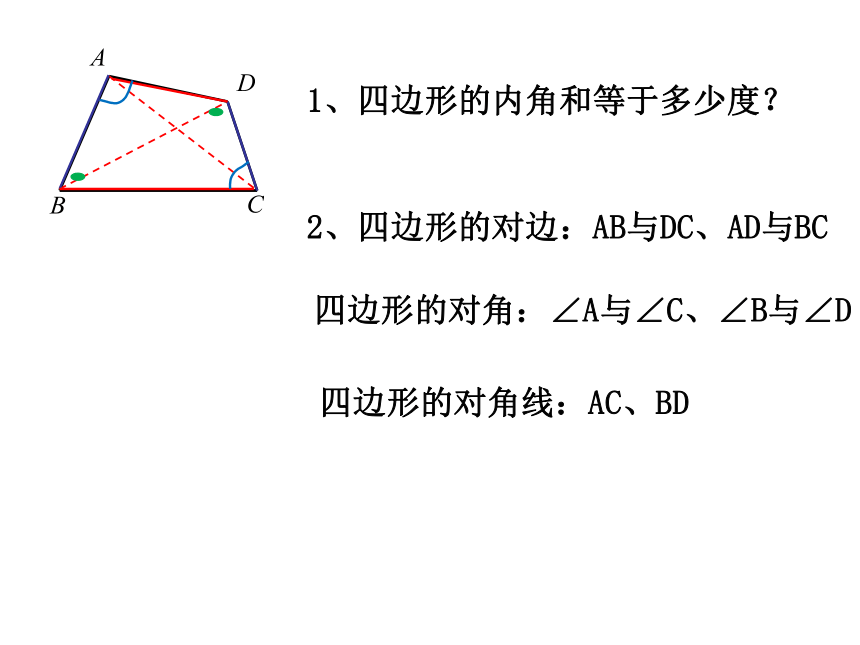
1、四边形的内角和等于多少度?
2、四边形的对边:AB与DC、AD与BC
四边形的对角:∠A与∠C、∠B与∠D
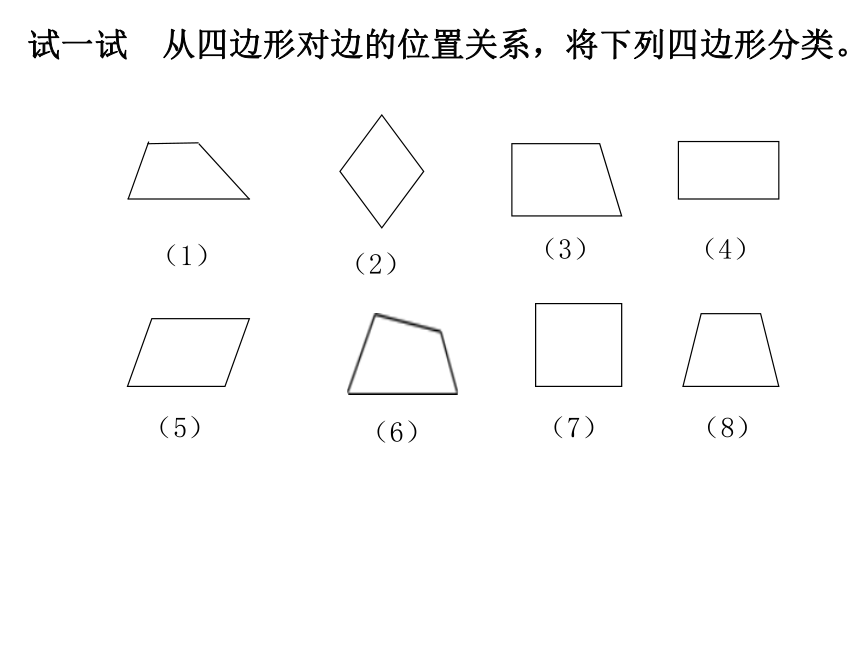
四边形的对角线:AC、BD试一试 从四边形对边的位置关系,将下列四边形分类。(1)(2)(3)(4)(5)(6)(7)(8)试一试 从四边形对边的位置关系,将下列四边形分类。两组对边都不平行一组对边平行,
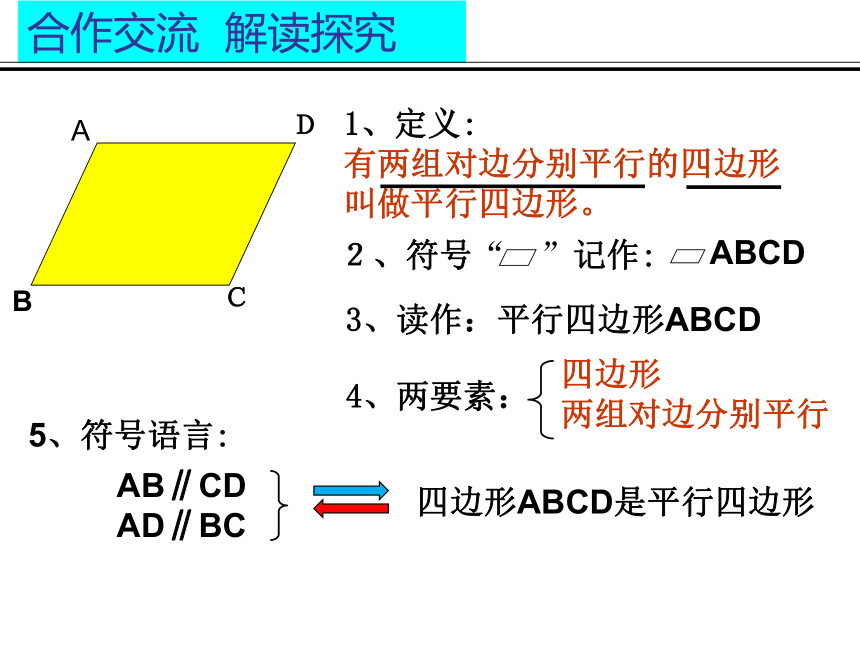
另一组对边不平行两组对边分别平行1、定义:
有两组对边分别平行的四边形 叫做平行四边形。2、符号“ ”记作:5、符号语言:
4、两要素: 四边形ABCD是平行四边形 ABCDAB∥CD AD∥BC3、读作:平行四边形ABCD平行四边形易变形晾衣架伸缩门汽车防护栏1.平行四边形的边具有哪些性质?2.平行四边形的角具有哪些性质?1:平行四边形的对边相等ABCD212:平行四边形的对角相等如何验证已知:如图 ABCD
求证:AB=CD,BC=DA;
∠A=∠C,∠B=∠D猜想:即∠BAD=∠DCB证明:联结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3ABCD方法小结:有关四边形的问题常常
可转化为三角形问题来处理。推论:夹在两条平行线间的平行线段相等观察思考∵AB∥CD,AD∥BC∴四边形ABCD是平行四边形(平行四边形的定义)∴AB=CD(平行四边形的对边相等)推论:夹在两条平行线间的平行线段相等观察思考∵AD∥BC,AB∥DC∴四边形ABCD是平行四边形(平行四边形的定义)∴AB=CD(平行四边形的对边相等)推论的符号语言:∴AB=CD(夹在两条平行线间的平行线段相等)观察思考ABBDCC两条平行线间的距离:
直线 上任意一点到直线 的距离都相等,因此把两条平行线中一条直线上任意一点到另一条直线的距离定义为两条平行线的距离。 例题1:一块平行四边形绿地,已知 ∠B =60° ,
求这个平行四边形绿地其他各内角的度数? 小结:平行四边形中已知其中一角可求出另外三个角的度数。变式1:一块平行四边形绿地,已知 ∠B =60° ,
求这个平行四边形绿地其他各内角的度数? ∠A 比∠B大60°,例2:一块平行四边形绿地,要在其四周围一圈栅栏,
,AB = DC=3米,AD =B C,
(平行四边形的对边相等)∵AB+DC+AD+BC=16米
∴ 2AD=10米∴ AD=5米,BC=5米答:其他三边分别是3米, 5米,5米.栅栏总长16米,若AB=3米,求其它三边的长分别是多少?小结:平行四边形中已知周长和一边,可求出另外三条边的长度。变式1:一块平行四边形绿地,要在其四周围一圈栅栏,
,AB = DC=3米,AD =B C,
(平行四边形的对边相等)∵AB+DC+AD+BC=16米
∴ 2AD=10米∴ AD=5米,BC=5米答:其他三边分别是3米, 5米,5米.栅栏总长16米,若AB=3米,求其它三边的长分别是多少?BC=3AB,求各边的长分别是多少?X米,=3X米,∴ 8X=16∴ X=2∴ AB=DC=2米,AD=BC=6米答:各边长分别是2米、2米、6米、6米.拓展:
已知点A(3,0)、B(-1,0)、C(0,2),
(1)若四边形ABCD是平行四边形,求D点坐标。
(2)若以A、B、C、D为顶点的四边形是平行四边形,求D点坐标。
小结:
1、找邻边、作平行线,定点
2、平移对边,找对应点,定坐标
课堂小结
1、平行四边形的定义
2、平行四边形的性质及其推论
3、平行四边形性质及其推论的作用?
4、所涉及的数学思想方法有哪些?
5、后续从哪些方面进一步研究和完善平行四边的性质?6.已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?(4,2)(2,-2)(– 4,2)课堂练习
——平行四边形的性质(1)
1、四边形的内角和等于多少度?
2、四边形的对边:AB与DC、AD与BC
四边形的对角:∠A与∠C、∠B与∠D
四边形的对角线:AC、BD试一试 从四边形对边的位置关系,将下列四边形分类。(1)(2)(3)(4)(5)(6)(7)(8)试一试 从四边形对边的位置关系,将下列四边形分类。两组对边都不平行一组对边平行,
另一组对边不平行两组对边分别平行1、定义:
有两组对边分别平行的四边形 叫做平行四边形。2、符号“ ”记作:5、符号语言:
4、两要素: 四边形ABCD是平行四边形 ABCDAB∥CD AD∥BC3、读作:平行四边形ABCD平行四边形易变形晾衣架伸缩门汽车防护栏1.平行四边形的边具有哪些性质?2.平行四边形的角具有哪些性质?1:平行四边形的对边相等ABCD212:平行四边形的对角相等如何验证已知:如图 ABCD
求证:AB=CD,BC=DA;
∠A=∠C,∠B=∠D猜想:即∠BAD=∠DCB证明:联结AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3ABCD方法小结:有关四边形的问题常常
可转化为三角形问题来处理。推论:夹在两条平行线间的平行线段相等观察思考∵AB∥CD,AD∥BC∴四边形ABCD是平行四边形(平行四边形的定义)∴AB=CD(平行四边形的对边相等)推论:夹在两条平行线间的平行线段相等观察思考∵AD∥BC,AB∥DC∴四边形ABCD是平行四边形(平行四边形的定义)∴AB=CD(平行四边形的对边相等)推论的符号语言:∴AB=CD(夹在两条平行线间的平行线段相等)观察思考ABBDCC两条平行线间的距离:
直线 上任意一点到直线 的距离都相等,因此把两条平行线中一条直线上任意一点到另一条直线的距离定义为两条平行线的距离。 例题1:一块平行四边形绿地,已知 ∠B =60° ,
求这个平行四边形绿地其他各内角的度数? 小结:平行四边形中已知其中一角可求出另外三个角的度数。变式1:一块平行四边形绿地,已知 ∠B =60° ,
求这个平行四边形绿地其他各内角的度数? ∠A 比∠B大60°,例2:一块平行四边形绿地,要在其四周围一圈栅栏,
,AB = DC=3米,AD =B C,
(平行四边形的对边相等)∵AB+DC+AD+BC=16米
∴ 2AD=10米∴ AD=5米,BC=5米答:其他三边分别是3米, 5米,5米.栅栏总长16米,若AB=3米,求其它三边的长分别是多少?小结:平行四边形中已知周长和一边,可求出另外三条边的长度。变式1:一块平行四边形绿地,要在其四周围一圈栅栏,
,AB = DC=3米,AD =B C,
(平行四边形的对边相等)∵AB+DC+AD+BC=16米
∴ 2AD=10米∴ AD=5米,BC=5米答:其他三边分别是3米, 5米,5米.栅栏总长16米,若AB=3米,求其它三边的长分别是多少?BC=3AB,求各边的长分别是多少?X米,=3X米,∴ 8X=16∴ X=2∴ AB=DC=2米,AD=BC=6米答:各边长分别是2米、2米、6米、6米.拓展:
已知点A(3,0)、B(-1,0)、C(0,2),
(1)若四边形ABCD是平行四边形,求D点坐标。
(2)若以A、B、C、D为顶点的四边形是平行四边形,求D点坐标。
小结:
1、找邻边、作平行线,定点
2、平移对边,找对应点,定坐标
课堂小结
1、平行四边形的定义
2、平行四边形的性质及其推论
3、平行四边形性质及其推论的作用?
4、所涉及的数学思想方法有哪些?
5、后续从哪些方面进一步研究和完善平行四边的性质?6.已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?(4,2)(2,-2)(– 4,2)课堂练习
