22.3 特殊的平行四边形——正方形课件(21张PPT)
文档属性
| 名称 | 22.3 特殊的平行四边形——正方形课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 394.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 16:20:02 | ||
图片预览








文档简介
(共20张PPT)
复习提问
矩形:________ 的_________ 是矩形
矩形的定义?
菱形的定义?
菱形:________ 的_________是菱形
有一个内角为直角
平行四边形
平行四边形
一组邻边相等
22.3(4)
正方形
有 的平行四边形叫做正方形。
一组邻边相等且有一个角是直角
判定2:有一个内角为直角的菱形正方形。
判定1:有一组邻边相等的矩形是正方形。
判定一个四边形是正方形我们就有三个方法
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
一组邻边相等一内角是直角
正方形是特殊的平行四边形,也是特殊的矩形,还是特殊的菱形。因此正方形既具有矩形的性质,又具有菱形的性质。
(2)边: ;
(3)角: ;
(4)对角线: ;
中心对称
轴对称
正方形的四条边都相等、对边平行
正方形的四个角都是直角
正方形的两条对角线相等,并且互相垂直平分,且每条对角线平分一组对角。
(1)对称性;正方形是_________图形
对称中心是_________ 、 正方形又是_________图形,有 对称轴,对称轴是 。
两条对角线的交点
两条对角线和每组对边中点连线所在直线。
4
请结合图形说出性质的几何表示
A
B
C
D
O
二、正方形的性质的应用
已知四边形ABCD是正方形,根据图形求出相应的x、y、z
X=________ ,
y=_________
z=__________
x=_______
y=________
(x表示AC的一半)
二、选择
正方形具有而矩形没有的性质是( )
(A)四个角相等 (B)对角线互相垂直平分
(C)对角线相等 (D)对角互补
三、判断对错
1、对角线互相垂直的矩形是正方形。( )
2、对角线相等的平行四边形是正方形。( )
×
√
B
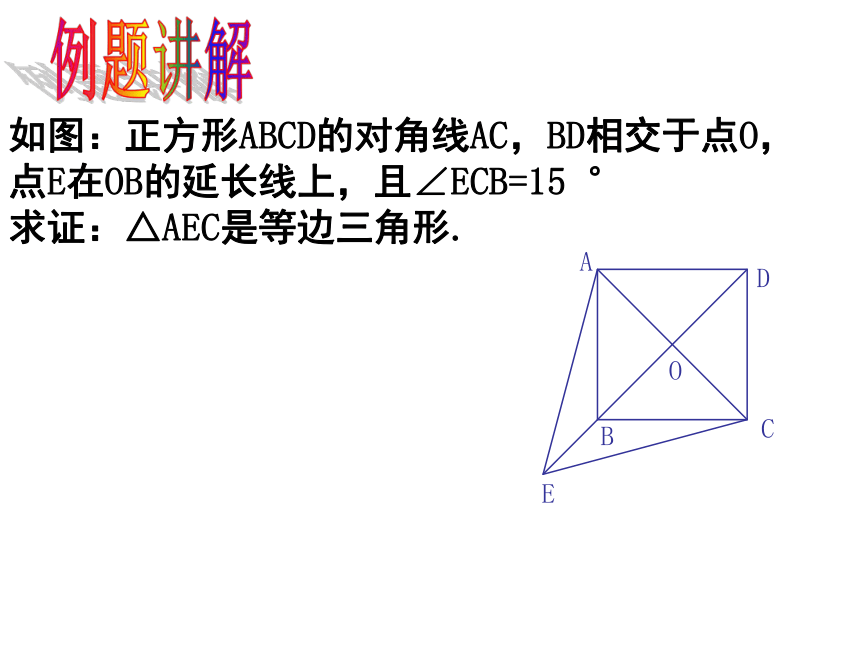
如图:正方形ABCD的对角线AC,BD相交于点O,点E在OB的延长线上,且∠ECB=15 °
求证:△AEC是等边三角形.
如图:正方形ABCD中,E是DB延长线一点,且∠ECB=15°
求证:EC=BD.
变式练习
2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.
A
B
C
D
E
F
1、通过这节课的学习活动
你知识上有哪些收获?
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
一组邻边相等一内角是直角
菱形
矩形
平行四边形
正
形
方
2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.
A
B
C
D
E
F
∴四边形ABCD是正方形(有一组邻边相等的矩形是正方形 )
∴ DE=DF
DE⊥AC, DF⊥BC
∵ CD平分∠ACB
∴ 四边形ABCD为矩形
而∠ACB=90°
∴ ∠DEC=90°, ∠DFC=90°
证明:∵ DE⊥AC,DF⊥AB
一、填空:1.已知正方形的边长为2cm则这个正方形的周长是 、对角线长 和正方形的面积是 .
2、正方形具有而矩形不一定具有的性质是( )
(A)四个角相等 (B)对角线互相垂直平分
(C)对角线相等 (D)对角互补
3、正方形具有而菱形不一定具有的性质是( )
(A)四条边相等 (B)对角线互相垂直平分
(C)对角线平分一组对角 (D)对角线相等
4.正方形有 条对称轴.
D
B
4
8
4
2
练行四边形 矩形 菱形
边
角
对角线
对称性
二、特殊四边形的性质
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
给你一张正方形的彩色纸,你能一刀剪出如图的正方形孔吗?拿起剪刀试一试。
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
平行四边形
正方形
一组邻边相等
一内角是直角
复习提问
矩形:________ 的_________ 是矩形
矩形的定义?
菱形的定义?
菱形:________ 的_________是菱形
有一个内角为直角
平行四边形
平行四边形
一组邻边相等
22.3(4)
正方形
有 的平行四边形叫做正方形。
一组邻边相等且有一个角是直角
判定2:有一个内角为直角的菱形正方形。
判定1:有一组邻边相等的矩形是正方形。
判定一个四边形是正方形我们就有三个方法
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
一组邻边相等一内角是直角
正方形是特殊的平行四边形,也是特殊的矩形,还是特殊的菱形。因此正方形既具有矩形的性质,又具有菱形的性质。
(2)边: ;
(3)角: ;
(4)对角线: ;
中心对称
轴对称
正方形的四条边都相等、对边平行
正方形的四个角都是直角
正方形的两条对角线相等,并且互相垂直平分,且每条对角线平分一组对角。
(1)对称性;正方形是_________图形
对称中心是_________ 、 正方形又是_________图形,有 对称轴,对称轴是 。
两条对角线的交点
两条对角线和每组对边中点连线所在直线。
4
请结合图形说出性质的几何表示
A
B
C
D
O
二、正方形的性质的应用
已知四边形ABCD是正方形,根据图形求出相应的x、y、z
X=________ ,
y=_________
z=__________
x=_______
y=________
(x表示AC的一半)
二、选择
正方形具有而矩形没有的性质是( )
(A)四个角相等 (B)对角线互相垂直平分
(C)对角线相等 (D)对角互补
三、判断对错
1、对角线互相垂直的矩形是正方形。( )
2、对角线相等的平行四边形是正方形。( )
×
√
B
如图:正方形ABCD的对角线AC,BD相交于点O,点E在OB的延长线上,且∠ECB=15 °
求证:△AEC是等边三角形.
如图:正方形ABCD中,E是DB延长线一点,且∠ECB=15°
求证:EC=BD.
变式练习
2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.
A
B
C
D
E
F
1、通过这节课的学习活动
你知识上有哪些收获?
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
一组邻边相等一内角是直角
菱形
矩形
平行四边形
正
形
方
2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.
A
B
C
D
E
F
∴四边形ABCD是正方形(有一组邻边相等的矩形是正方形 )
∴ DE=DF
DE⊥AC, DF⊥BC
∵ CD平分∠ACB
∴ 四边形ABCD为矩形
而∠ACB=90°
∴ ∠DEC=90°, ∠DFC=90°
证明:∵ DE⊥AC,DF⊥AB
一、填空:1.已知正方形的边长为2cm则这个正方形的周长是 、对角线长 和正方形的面积是 .
2、正方形具有而矩形不一定具有的性质是( )
(A)四个角相等 (B)对角线互相垂直平分
(C)对角线相等 (D)对角互补
3、正方形具有而菱形不一定具有的性质是( )
(A)四条边相等 (B)对角线互相垂直平分
(C)对角线平分一组对角 (D)对角线相等
4.正方形有 条对称轴.
D
B
4
8
4
2
练行四边形 矩形 菱形
边
角
对角线
对称性
二、特殊四边形的性质
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
给你一张正方形的彩色纸,你能一刀剪出如图的正方形孔吗?拿起剪刀试一试。
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
平行四边形
正方形
一组邻边相等
一内角是直角
