人教版七年级数学下册 5.1.1 相交线提升训练试题(含解析)
文档属性
| 名称 | 人教版七年级数学下册 5.1.1 相交线提升训练试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 17:02:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.1.1相交线
1.有一条 ,另一边互为反向 的两个角叫做邻补角;
有一个公共的 ,两边分别互为反向 的两个角叫做对顶角。
2.邻补角 ,对顶角 。
如图,直线a,b相交所成的四个角中,∠1= ,
∠2= ,∠1+∠2= ,∠3+∠4= 。
3.方法技巧
(1)判断两个角是否互为对顶角的关键是看这两个角是否有公共顶点,一个角的两边是否为另一个角两的边反向延长线。
(2)判断两个角是否互为邻补角,关键要看这两个角的两边,其中一边是否是公共边,另外两边是否互为反向延长线。
【例1】如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE
(1)若∠AOC=76,求∠BOF的度数
(2)若∠BOF=36°,求∠AOC的度数
(3)请探究∠AOC与∠BOF的数量关系
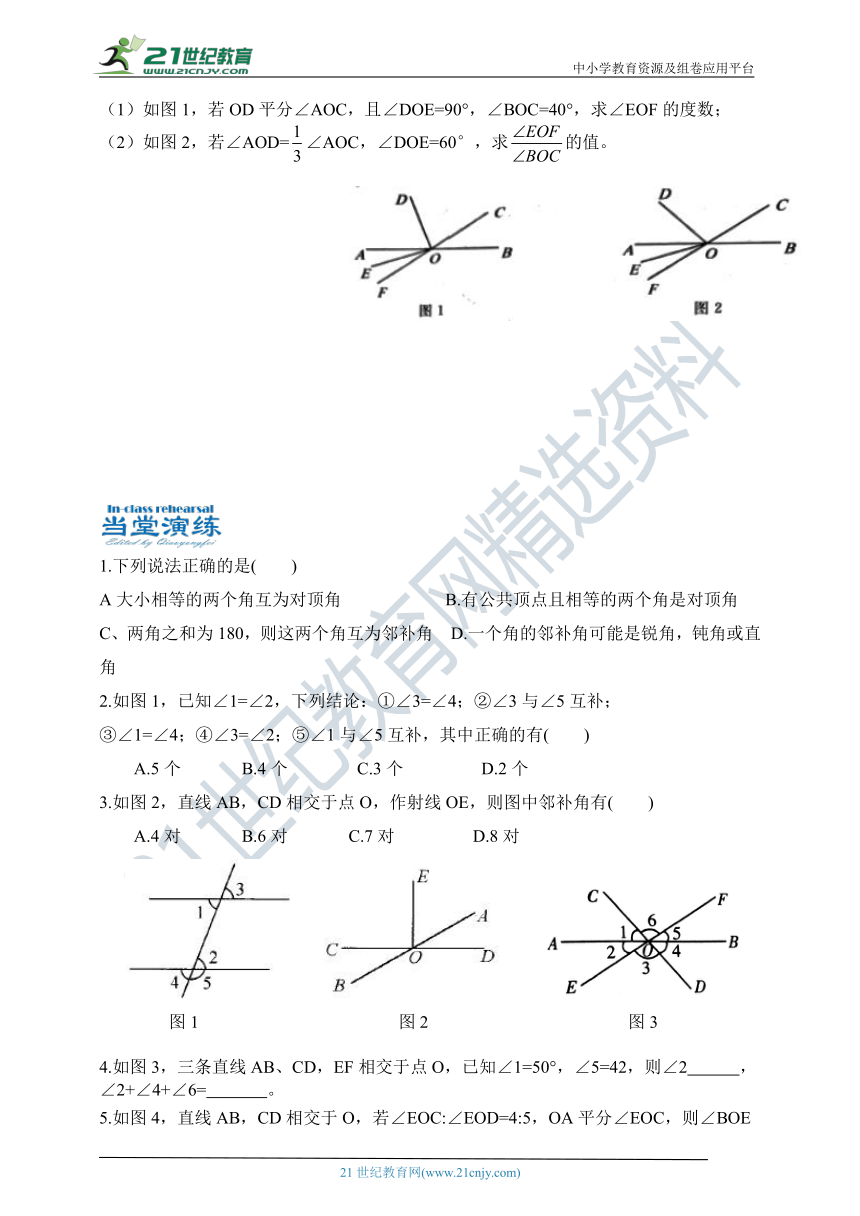
【例2】已知直线AB与直线CF交于点O。
(1)如图1,若OD平分∠AOC,且∠DOE=90°,∠BOC=40°,求∠EOF的度数;
(2)如图2,若∠AOD=∠AOC,∠DOE=60°,求的值。
1.下列说法正确的是( )
A大小相等的两个角互为对顶角 B.有公共顶点且相等的两个角是对顶角
C、两角之和为180,则这两个角互为邻补角 D.一个角的邻补角可能是锐角,钝角或直角
2.如图1,已知∠1=∠2,下列结论:①∠3=∠4;②∠3与∠5互补;
③∠1=∠4;④∠3=∠2;⑤∠1与∠5互补,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
3.如图2,直线AB,CD相交于点O,作射线OE,则图中邻补角有( )
A.4对 B.6对 C.7对 D.8对
图1 图2 图3
4.如图3,三条直线AB、CD,EF相交于点O,已知∠1=50°,∠5=42,则∠2 ,
∠2+∠4+∠6= 。
5.如图4,直线AB,CD相交于O,若∠EOC:∠EOD=4:5,OA平分∠EOC,则∠BOE
= 。
6.如图5,AD、BE、CF相交于点O,∠AOC=120°,∠BOD=130°,则∠EOF的度数为 。
图4 图5
7.如图,直线AB、CD相交于点O。
(1)若∠AOD比∠AOC大40°,求∠BOD的度数
(2)若∠AOD:∠AOC=3:2,求∠BOD的度数
13.如图,直线AB,CD相交于点O,∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE的大小
14.如图,直线AB,CD相交于O,OA平分∠EOC,若∠EOA:∠EOD=1:3,求∠BOD
的度数。
5.1.1相交线参考答案
1.有一条 公共边 ,另一边互为反向 延长线 的两个角叫做邻补角;
有一个公共的 顶点 ,两边分别互为反向 延长线 的两个角叫做对顶角。
2.邻补角 互补 ,对顶角 相等 。
如图,直线a,b相交所成的四个角中,∠1= ∠3 ,
∠2= ∠4 ,∠1+∠2= 180° ,∠3+∠4= 180° 。
3.方法技巧
(1)判断两个角是否互为对顶角的关键是看这两个角是否有公共顶点,一个角的两边是否为另一个角两的边反向延长线。
(2)判断两个角是否互为邻补角,关键要看这两个角的两边,其中一边是否是公共边,另外两边是否互为反向延长线。
【例1】如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE
(1)若∠AOC=76,求∠BOF的度数
(2)若∠BOF=36°,求∠AOC的度数
(3)请探究∠AOC与∠BOF的数量关系
【解析】
(1)∵∠BOD=∠AOC=76?,又∵OE平分∠BOD,
∴∠DOE=∠BOD=12×76?=38?.
∴∠COE=180??∠DOE=180??38?=142?,
∵OF平分∠COE, ∴∠EOF=∠COE=×142?=71?,
∴∠BOF=∠EOF?∠BOE=71??38?=33?.
(2)∵OE平分∠BOD,OF平分∠COE,
∴∠BOE=∠EOD,∠COF=∠FOE,
∴设∠BOE=x,则∠DOE=x,故∠COA=2x,∠EOF=∠COF=x+36?,
则∠AOC+∠COF+∠BOF=2x+x+36?+36?=180?,
解得:x=36?,故∠AOC=72?.
(3)
【例2】已知直线AB与直线CF交于点O。
(1)如图1,若OD平分∠AOC,且∠DOE=90°,∠BOC=40°,求∠EOF的度数;
(2)如图2,若∠AOD=∠AOC,∠DOE=60°,求的值。
【解析】
(1).
平分
答:的度数为.
(2)
1.下列说法正确的是( D )
A大小相等的两个角互为对顶角 B.有公共顶点且相等的两个角是对顶角
C、两角之和为180,则这两个角互为邻补角 D.一个角的邻补角可能是锐角,钝角或直角
2.如图1,已知∠1=∠2,下列结论:①∠3=∠4;②∠3与∠5互补;
③∠1=∠4;④∠3=∠2;⑤∠1与∠5互补,其中正确的有( A )
A.5个 B.4个 C.3个 D.2个
3.如图2,直线AB,CD相交于点O,作射线OE,则图中邻补角有( B )
A.4对 B.6对 C.7对 D.8对
图1 图2 图3
4.如图3,三条直线AB、CD,EF相交于点O,已知∠1=50°,∠5=42°,则∠2= 42° ,
∠2+∠4+∠6= 180° 。
5.如图4,直线AB,CD相交于O,若∠EOC:∠EOD=4:5,OA平分∠EOC,则∠BOE
= 140° 。
6.如图5,AD、BE、CF相交于点O,∠AOC=120°,∠BOD=130°,则∠EOF的度数为 70° 。
图4 图5
7.如图,直线AB、CD相交于点O。
(1)若∠AOD比∠AOC大40°,求∠BOD的度数
(2)若∠AOD:∠AOC=3:2,求∠BOD的度数
【解答】(1)设∠AOC=x,则∠AOD=x+40°,
∴x+(x+40°)=180°,
∴∠BOD=x=70°.
(2)设∠AOD=3x,∠AOC=2x,
∴3x+2x=180°,x=36°,
∴∠BOD=∠AOC=72°.
13.如图,直线AB,CD相交于点O,∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE的大小
∵∠AOC与∠DOE是对顶角,∠AOC=80?,
∴∠DOB=80?,
∵∠BOE:∠EOD=2:3,
∴∠EOD=80?×=48?,
∵∠AOD与∠AOC互为邻补角,
∴∠AOD=180??∠AOC=180??80?=100?
∴∠AOE=∠AOD+∠EOD=100?+48?=148?
14.如图,直线AB,CD相交于O,OA平分∠EOC,若∠EOA:∠EOD=1:3,求∠BOD
的度数。
【解析】
∵OA平分∠EOC
∴∠AOC=∠EOA
设∠EOA=x,则∠AOC=x,∠EOD=3x
∵∠AOC+∠EOA+∠EOD=180°
∴x+x+3x=180° 解得x=36°
∴∠BOD=∠AOC=36°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
