人教版七年级数学下册 5.2.2 平行线的判定提升训练试题(2)(含解析)
文档属性
| 名称 | 人教版七年级数学下册 5.2.2 平行线的判定提升训练试题(2)(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 19:04:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.2.2平行线的判定(2)
【例1】如图,已知∠B=25°,∠ECD=45°,∠BEC=70°,试说明:AB∥CD
【例2】(1)尝试:如图1,点B,C,D在同一直线上,∠A=∠1=∠3=55°,∠E=∠2=35°,试说明AB∥DE;
(2)应用:如图2,点B,C,D在同一直线上,AC⊥EC,∠A=∠1,∠E=∠2,试说明AB∥DE。
1.同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A.a∥d B.b⊥d C.a⊥d D.b∥c
2.如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠D=∠ACB,其中正确的有( )
A.1个 B.2个 C.3个 D.0个
3.如图,已知∠1=∠2=∠3=∠4,则图中所有平行的直线有( )
A.AB∥CD∥EF B.CD∥EF
C.AB∥EF D.AB∥CD∥EF,BC∥DE
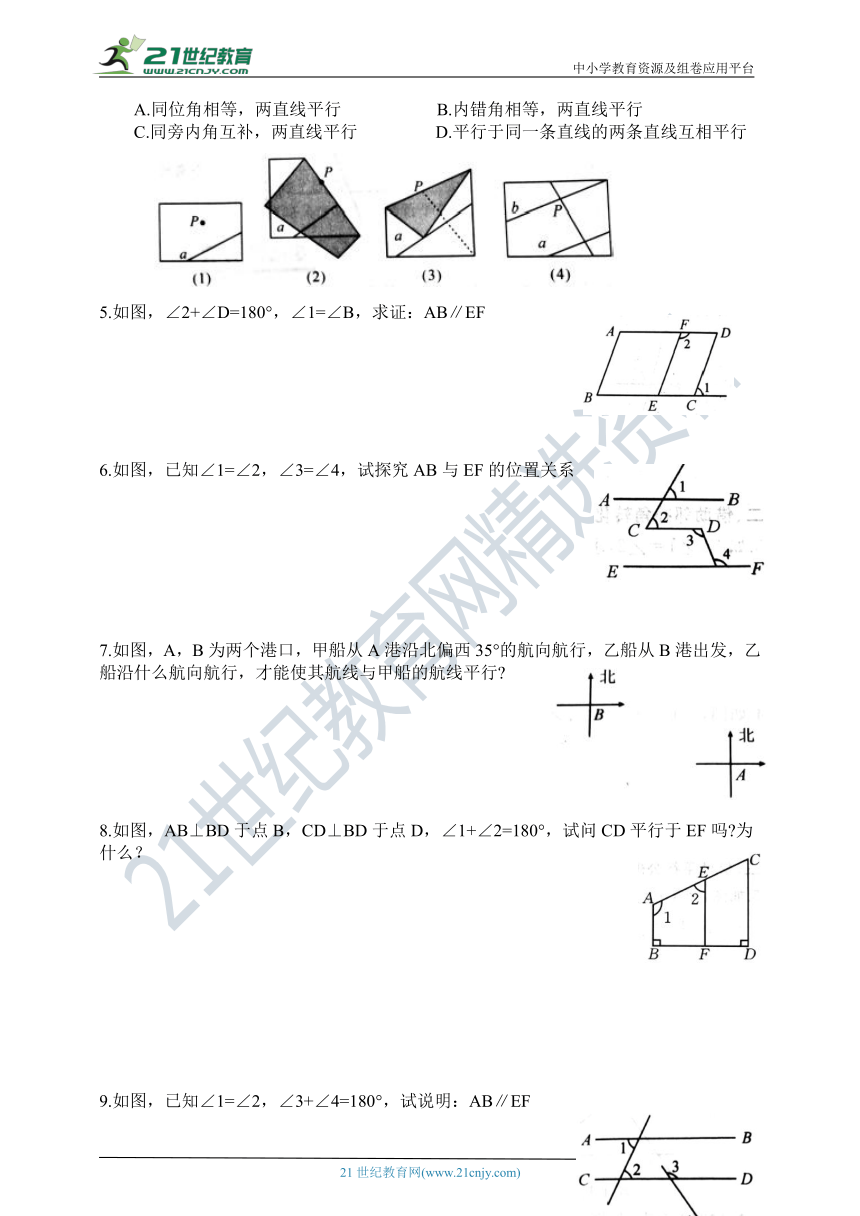
4.我们可以用如图所示的方法过直线a外的一点P折出直线a的平行线b,下列判定不能作为这种方法的依据的是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.平行于同一条直线的两条直线互相平行
5.如图,∠2+∠D=180°,∠1=∠B,求证:AB∥EF
6.如图,已知∠1=∠2,∠3=∠4,试探究AB与EF的位置关系
7.如图,A,B为两个港口,甲船从A港沿北偏西35°的航向航行,乙船从B港出发,乙船沿什么航向航行,才能使其航线与甲船的航线平行?
8.如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD平行于EF吗?为什么?
9.如图,已知∠1=∠2,∠3+∠4=180°,试说明:AB∥EF
5.2.2平行线的判定(2)参考答案
【例1】如图,已知∠B=25°,∠ECD=45°,∠BEC=70°,试说明:AB∥CD
证明:
过点E作 EF∥AB
∴∠BEF=∠B=25°
∴∠CEF=∠BEC-∠BEF=70°-25°=45°
∵∠ECD=45°
∴∠CEF=∠ECF
∴EF∥CD
又EF∥AB
∴AB∥CD
【例2】(1)尝试:如图1,点B,C,D在同一直线上,∠A=∠1=∠3=55°,∠E=∠2=35°,试说明AB∥DE;
(2)应用:如图2,点B,C,D在同一直线上,AC⊥EC,∠A=∠1,∠E=∠2,试说明AB∥DE。
【解析】
(1)∵∠A=∠1=∠3=55°
∴∠B=180°-∠A-∠1=70°
∵∠E=∠2=35°
∴∠D=180°-∠E-∠2=110°
∴∠B+∠D=70°+110°=180
∴AB∥DE
(2)∵AC⊥EC
∴∠ACE=90°
∴∠1+∠2=180°-∠ACE=90°
∵∠A=∠1,∠E=∠2
∴∠B=180°-2∠1,∠D=180°-2∠2
∴∠B+∠D=180°-2∠1+180°-2∠2=360°-2(∠1+∠2)=180°
∴AB∥DE
1.同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( C )
A.a∥d B.b⊥d C.a⊥d D.b∥c
2.如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠D=∠ACB,其中正确的有( B )
A.1个 B.2个 C.3个 D.0个
3.如图,已知∠1=∠2=∠3=∠4,则图中所有平行的直线有( D )
A.AB∥CD∥EF B.CD∥EF
C.AB∥EF D.AB∥CD∥EF,BC∥DE
4.我们可以用如图所示的方法过直线a外的一点P折出直线a的平行线b,下列判定不能作为这种方法的依据的是( D )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.平行于同一条直线的两条直线互相平行
5.如图,∠2+∠D=180°,∠1=∠B,求证:AB∥EF
证明:∵∠2+∠D=180?,
∴EF∥DC,
∵∠1=∠B,
∴AB∥DC,
∴AB∥EF.
6.如图,已知∠1=∠2,∠3=∠4,试探究AB与EF的位置关系
结论:AB∥EF.
理由:∵∠1=∠2,
∴AB∥CD,
∵∠3=∠4,
∴CD∥EF,
∴AB∥EF.
7.如图,A,B为两个港口,甲船从A港沿北偏西35°的航向航行,乙船从B港出发,乙船沿什么航向航行,才能使其航线与甲船的航线平行?
【解析】①当它们航行的方向一致,即乙船从B港出发,乙船从B港沿北偏西35?的航向航行时,甲、乙两船的航线平行;
②当它们航行的方向相反时,即乙船从B港出发,乙船从B港沿南偏东35?的航向航行时,甲、乙两船的航线平行;
综上所述,乙船沿北偏西35?或南偏东35?航向航行,使其航线与甲船的航线平行。
8.如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD平行于EF吗?为什么?
【解析】平行。
∵AB⊥BD,CD⊥BD,
∴AB∥CD,
∵∠1+∠2=180?,
∴AB∥EF,
∴CD∥EF.
9.如图,已知∠1=∠2,∠3+∠4=180°,试说明:AB∥EF
证明:如图,∵∠1=∠2,
∴AB∥CD.
∵∠3+∠4=180?,
∴CD∥EF,
∴AB∥EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
