人教版七年级数学下册 5.3.1 平行线的性质提升训练试题(1)(含解析)
文档属性
| 名称 | 人教版七年级数学下册 5.3.1 平行线的性质提升训练试题(1)(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 19:07:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.3.1平行线的性质(1)
1.两条平行线被第三条直线所截,同位角 ;可简说成:两直线平行, 。
2.两条平行线被第三条直线所截,内错角 ;可简说成:两直线平行, 。
3两条平行线被第三条直线所截,同旁内角 ;可简说成:两直线平行, 。
4.如图,已知a∥b,则∠1 ∠2,∠2 ∠3,∠2+∠4= 。
【例1】如图1,已知点D为∠ABC内一点,点E为线段BC上一点,连DE、CD,AE,且∠AED=∠A+∠D。
(1)求证:AB∥CD;
(2)如图2,过点A的直线MA∥ED,猜想并验证∠MAB与∠CDE的数量关系
【例2】如图,已知AB∥CD,点P在CD下方。求证:∠APC=∠BAP-∠DCP
1.如图1,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果
∠1=27°,那么∠2的度数为( )
A.53° B.55° C.57° D.60°
2.如图2,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐角∠A=120°,第二次拐角∠B=150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数为( )
A.120° B.130° C.150° D.165°
图1 图2 图3
3.如图3,AB∥CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于( )
A.26° B.52° C.54° D.77°
4.如图4,已知∠1=∠2,∠D=78°,则∠BCD的度数为 。
5.如图5,已知AB∥CD,∠ABC=∠ADC,则下列结论:①BC∥AD;②∠EAC+∠HCF=180°;③若AD平分∠EAC,则CF平分∠HCG;④S四边形ABCD=2S三角形ABC,其中正确结论的序号是 。
图4 图5 图6
6.如图6,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE的度数为 。
7.已知∠1的两边分别与∠2的两边平行,若∠1=40°,求∠2的度数
8.如图,点B,E分别是AC,DF上一点,连BD,CE分别交AF于G,H,∠1=∠2
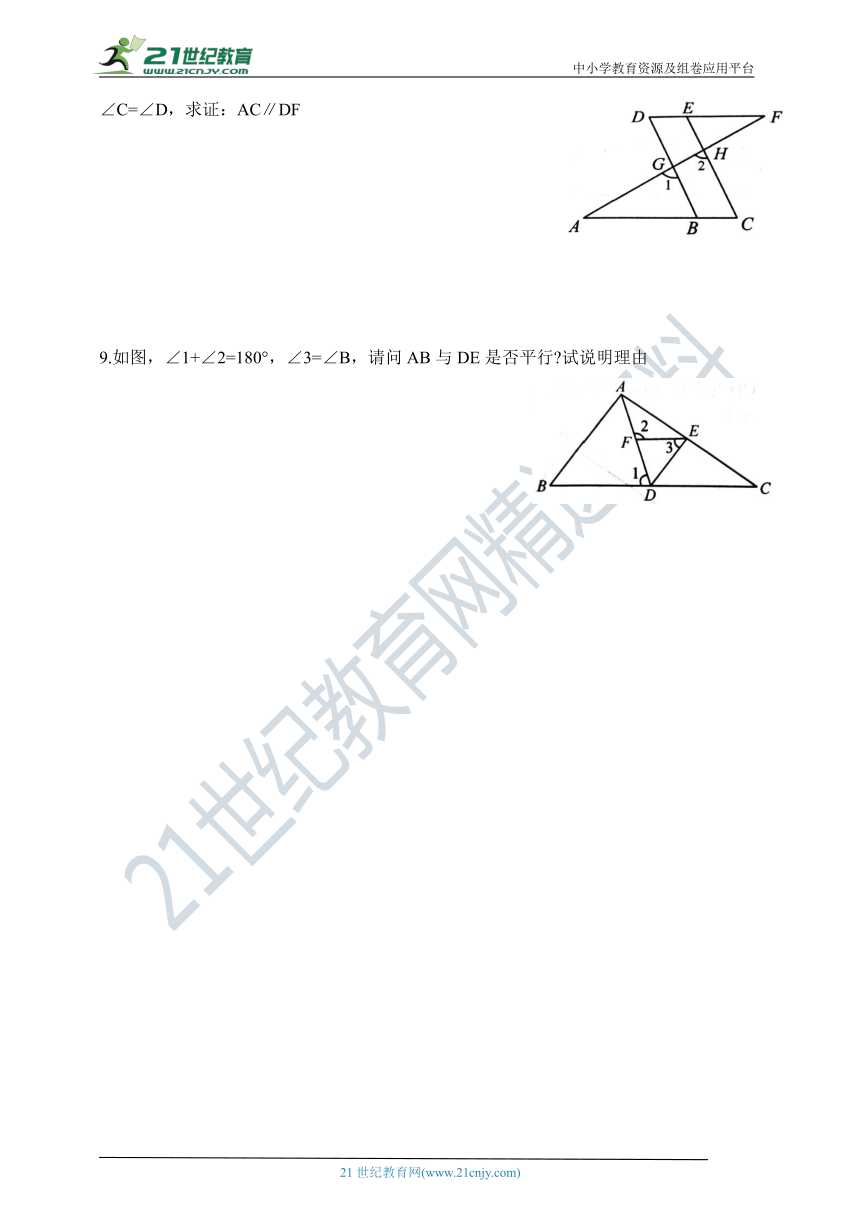
∠C=∠D,求证:AC∥DF
9.如图,∠1+∠2=180°,∠3=∠B,请问AB与DE是否平行?试说明理由
5.3.1平行线的性质(1)参考答案
1.两条平行线被第三条直线所截,同位角 相等 ;可简说成:两直线平行, 同位角相等 。
2.两条平行线被第三条直线所截,内错角 相等 ;可简说成:两直线平行, 内错角相等 。
3两条平行线被第三条直线所截,同旁内角 互补 ;可简说成:两直线平行, 同旁内角互补 。
4.如图,已知a∥b,则∠1 = ∠2,∠2 = ∠3,∠2+∠4= 180° 。
【例1】如图1,已知点D为∠ABC内一点,点E为线段BC上一点,连DE、CD,AE,且∠AED=∠A+∠D。
(1)求证:AB∥CD;
(2)如图2,过点A的直线MA∥ED,猜想并验证∠MAB与∠CDE的数量关系
【解析】(1)过点E作EF∥AB
∵EF∥AB
∴∠A=∠AEF,
∵∠AED=∠AEF+∠FED=∠A+∠D
∴∠FED=∠D
∴EF∥CD
∴AB∥CD
(2)∠MAB与∠CDE的数量关系是:∠MAB=∠CDE,
理由过点B作BF∥AM交CD的延长线于F,∴∠MAB=∠ABF
∵AB∥CD ∴∠ABF=∠BFC
∵AE∥ED ∴BF∥ED ∴∠BFC=∠CDE ∴∠MAB=∠CDE
【例2】如图,已知AB∥CD,点P在CD下方。 求证:∠APC=∠BAP-∠DCP
【解析】
(1)如图1,过点A作AN∥PC交CD于N
∴∠APC=∠PAN,∠DCP=∠ANC
∵AB∥CD ∴∠ANC=∠BAN
∴∠DCP=∠BAN
∵∠PAN=∠BAP-∠BAN
∴∠APC=∠BAP-∠DCP
1.如图1,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果
∠1=27°,那么∠2的度数为( C )
A.53° B.55° C.57° D.60°
2.如图2,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐角∠A=120°,第二次拐角∠B=150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数为( C )
A.120° B.130° C.150° D.165°
图1 图2 图3
3.如图3,AB∥CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于( B )
A.26° B.52° C.54° D.77°
4.如图4,已知∠1=∠2,∠D=78°,则∠BCD的度数为 102° 。
5.如图5,已知AB∥CD,∠ABC=∠ADC,则下列结论:①BC∥AD;②∠EAC+∠HCF=180°;③若AD平分∠EAC,则CF平分∠HCG;④S四边形ABCD=2S三角形ABC,其中正确结论的序号是 ①②④ 。
图4 图5 图6
6.如图6,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE的度数为 20° 。
7.已知∠1的两边分别与∠2的两边平行,若∠1=40°,求∠2的度数
【解析】如图1,
∵∠1与∠2的两边分别平行,∠1=40?,
∴∠1=∠3,∠2=∠3,
∴∠1=∠2=40?,;
如图2,
∵∠1与∠2的两边分别平行,∠1=40?,
∴∠3=∠1=40?,
∴∠2=180??∠3=180??40?=140?
综上所述,∠2的度数等于40?或140?.
8.如图,点B,E分别是AC,DF上一点,连BD,CE分别交AF于G,H,∠1=∠2
∠C=∠D,求证:AC∥DF
【解析】
∵∠1=∠2, ∴BD∥EC, ∴∠C=∠DBA,
又∵∠C=∠D, ∴∠D=∠DBA,
∴AC∥DF
9.如图,∠1+∠2=180°,∠3=∠B,请问AB与DE是否平行?试说明理由
【解析】结论:AB∥DE.
理由:∵∠1+∠ADC=180?(平角的定义),
又∵∠1+∠2=180?(已知),
∴∠ADC=∠2(等量代换),
∴EF∥DC(同位角相等两直线平行),
∴∠3=∠EDC(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠EDC=∠B(等量代换),
∴AB∥DE(同位角相等两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
