人教版七年级数学下册 5.3.1 平行线的性质提升训练试题(2)(含解析)
文档属性
| 名称 | 人教版七年级数学下册 5.3.1 平行线的性质提升训练试题(2)(含解析) | 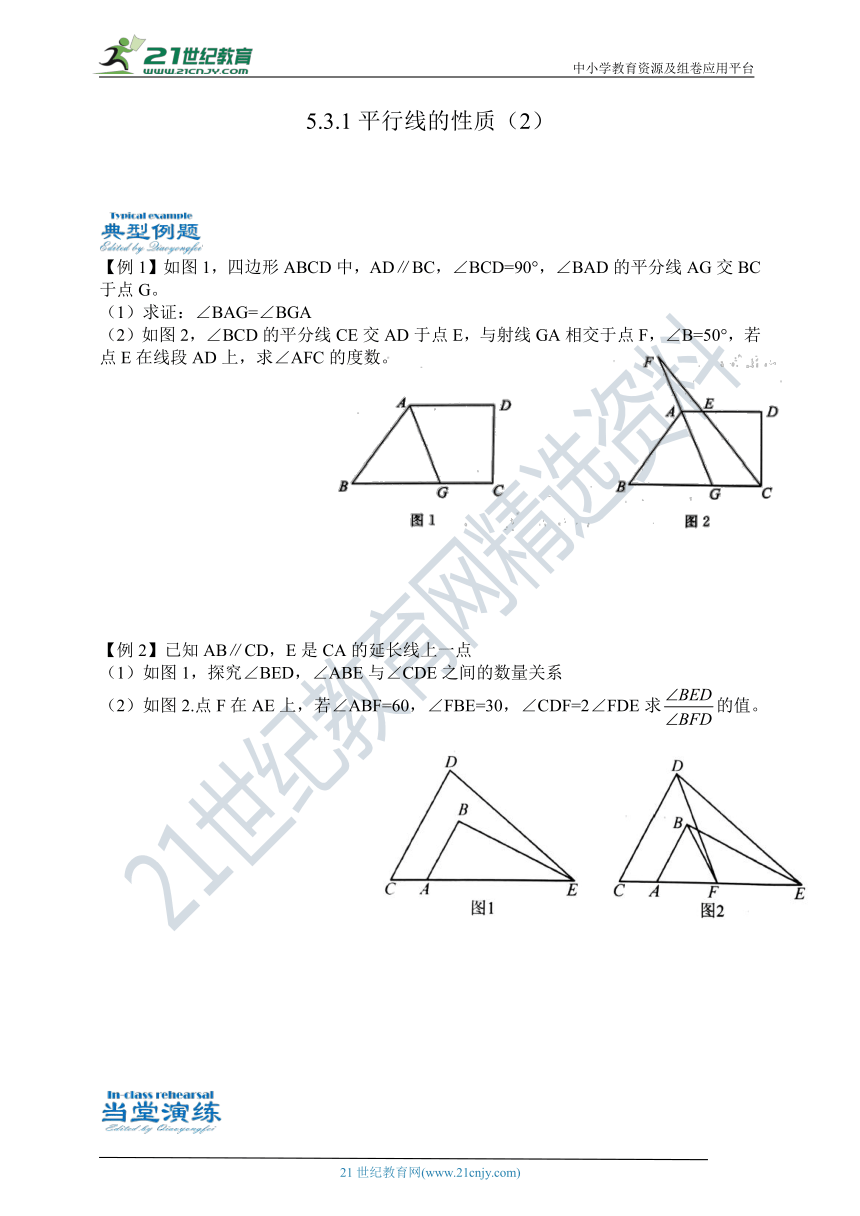 | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-15 19:09:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.3.1平行线的性质(2)
【例1】如图1,四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G。
(1)求证:∠BAG=∠BGA
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°,若点E在线段AD上,求∠AFC的度数。
【例2】已知AB∥CD,E是CA的延长线上一点
(1)如图1,探究∠BED,∠ABE与∠CDE之间的数量关系
(2)如图2.点F在AE上,若∠ABF=60,∠FBE=30,∠CDF=2∠FDE求的值。
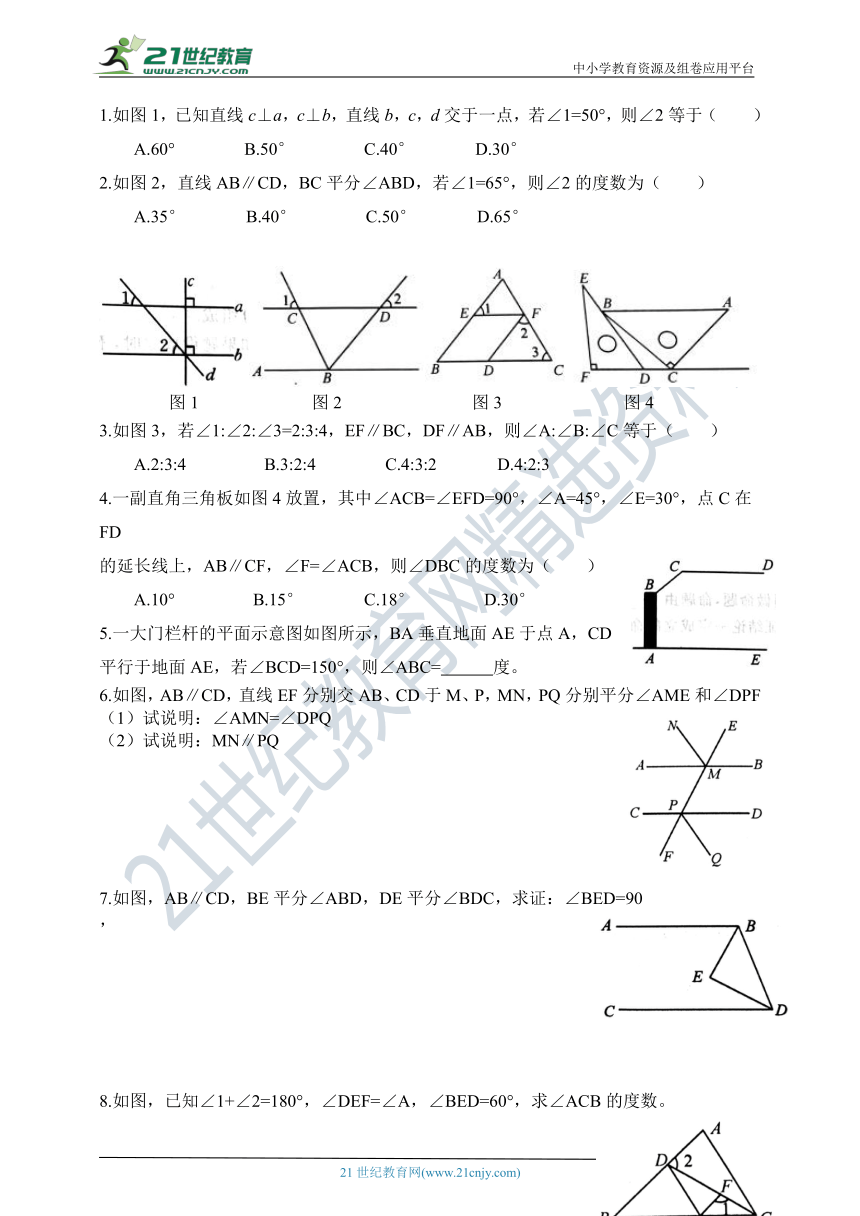
1.如图1,已知直线c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( )
A.60° B.50° C.40° D.30°
2.如图2,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的度数为( )
A.35° B.40° C.50° D.65°
图1 图2 图3 图4
3.如图3,若∠1:∠2:∠3=2:3:4,EF∥BC,DF∥AB,则∠A:∠B:∠C等于( )
A.2:3:4 B.3:2:4 C.4:3:2 D.4:2:3
4.一副直角三角板如图4放置,其中∠ACB=∠EFD=90°,∠A=45°,∠E=30°,点C在FD
的延长线上,AB∥CF,∠F=∠ACB,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
5.一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC= 度。
6.如图,AB∥CD,直线EF分别交AB、CD于M、P,MN,PQ分别平分∠AME和∠DPF
(1)试说明:∠AMN=∠DPQ
(2)试说明:MN∥PQ
7.如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,求证:∠BED=90
,
8.如图,已知∠1+∠2=180°,∠DEF=∠A,∠BED=60°,求∠ACB的度数。
9.如图,在四边形ABCD中,AD∥BC,∠1=∠2,∠3=∠4,求证:AB∥CD。
5.3.1平行线的性质(2)参考答案
【例1】如图1,四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G。
(1)求证:∠BAG=∠BGA
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°,若点E在线段AD上,求∠AFC的度数。
【解析】(1)∵AD∥BC,
∴∠GAD=∠AGB.
∵AG平分∠BAD,
∴∠BAG=∠GAD
∴∠BAG=∠BGA
(2)①过点F作FH∥AD.
∵AD∥BC, ∴∠B+∠BAD=180
∵∠B=50° ∴∠BAD=130°
∵AG平分∠BAD, ∴∠GAD=∠BAD ∴∠GAD=65°
∵CE平分∠BCD, ∴∠BCE=∠BCD.
∵∠BCD=90°, ∴∠BCE=45°.
∵AD∥BC ∴FH∥BC. ∴∠CFH=∠FCB. ∴∠CFH=45°.
∵FH∥AD, ∴∠GFH=∠GAD
【例2】已知AB∥CD,E是CA的延长线上一点
(1)如图1,探究∠BED,∠ABE与∠CDE之间的数量关系
(2)如图2,点F在AE上,若∠ABF=60°,∠FBE=30°,∠CDF=2∠FDE求的值
【解析】(1)如图,延长EB交CD于F。
∵AB∥CD ∴∠ABE=∠CFB
∵∠CFB+∠DFE=180°,∠BED+∠DFE+∠CDE=180°
∴∠CFB=∠BED+∠CDE
∴∠ABE=∠BED+∠CDE
(2)由(1)∵∠ABF=60°,∠FBE=30°,
∴∠ABE=∠ABF+∠FBE=60°+30°=90°
∵∠CDF=2∠FDE ∴∠CDE=∠CDF+∠FDE=3∠FDE
由(1)可知:∠CDE+∠BED=∠ABE
∴3∠FDE+∠BED=90°,即∠BED=90°-3∠FDE
又由(1)可知:∠BFD+∠CDF=∠ABF
∴∠BFD+2∠FDE=60°,即∠BFD=60°-2∠FDE
∴
1.如图1,已知直线c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( B )
A.60° B.50° C.40° D.30°
2.如图2,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的度数为( C )
A.35° B.40° C.50° D.65°
图1 图2 图3 图4
3.如图3,若∠1:∠2:∠3=2:3:4,EF∥BC,DF∥AB,则∠A:∠B:∠C等于( B )
A.2:3:4 B.3:2:4 C.4:3:2 D.4:2:3
4.一副直角三角板如图4放置,其中∠ACB=∠EFD=90°,∠A=45°,∠E=30°,点C在FD
的延长线上,AB∥CF,∠F=∠ACB,则∠DBC的度数为( B )
A.10° B.15° C.18° D.30°
5.一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC= 120 度。
6.如图,AB∥CD,直线EF分别交AB、CD于M、P,MN,PQ分别平分∠AME和∠DPF
(1)试说明:∠AMN=∠DPQ
(2)试说明:MN∥PQ
【解析】∵AB∥CD ∴∠AME=∠CPM=∠DPF,∠AMP=∠DPM
∵∠AMN=∠AME,∠DPQ=∠DPF,
∴∠AMN=∠DPQ,
∴∠AMN+∠AMP=∠DPQ+∠DPM,即∠NMP=∠MPQ,
∴MN∥PQ
7.如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,求证:∠BED=90°
【解析】过E作EF∥AB,
∵AB∥CD, ∴∠ABD+∠BDC=180°,
∵BE平分∠ABD, ∴∠ABD=2∠ABE,
∵DE平分∠BDC, ∴∠BDC=2∠CDE,
∴∠ABE+∠CDE=90°,
∵AB∥CD∥EF, ∴∠ABE=∠BEF,∠CDE=∠DEF,
∴∠BED=∠BEF+∠DEF=90°
8.如图,已知∠1+∠2=180°,∠DEF=∠A,∠BED=60°,求∠ACB的度数。
【解析】∵∠1+∠2=180° ∠2+∠BCD=180°
∴∠BDC=∠1
∴EF∥AB
∴∠DEF=∠BDE
∵∠DEF=∠A
∴BDE=∠A
∴DE∥AC
∴∠ACB=∠BED=60°
9.如图,在四边形ABCD中,AD∥BC,∠1=∠2,∠3=∠4,求证:AB∥CD。
证明:∵∠1=∠2 ∴∠1+∠EBD=∠2+∠EBD
∴∠ABD=∠EBC
∵AD∥BC ∴∠4=∠EBC
∴∠4=∠ABD
∵∠3=∠4
∴∠3=∠ABD
∴AB∥CD
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
